算数の合否を分けた一題
桜蔭中入試対策・算数の合否を分けた一題(2019年度)
難易度分類
| Ⅰ | (1)A (2)アA イA (3)アB イB ウB |
|---|---|
| Ⅱ | (1)①B ②B (2)①A ②アA イA ウA エA |
| Ⅲ | (1)①A (2)A |
| Ⅳ | (1)アC イC (2)C (3)C |
A:桜蔭合格を目指すなら必ず得点すべき問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題 ⇒ 合否を分ける問題
C:難易度や処理量から判断して、得点できなくても合否に影響しない問題
問題別寸評
(1)
昨年度より2題から1題に減った冒頭の計算問題。
今年度も1題でした。ただし、昨年度は逆算でしたが、今年度は順算。
計算過程で分母が2桁、3桁の数になるとはいえ、桜蔭の計算問題としては易しめ。
確実に得点することが求められます。
(2)①②
日暦算。うるう年が絡みます。
今年の5/1に元号が変更されることから、日暦算は旬のテーマです。
問題文中の但し書きには「次にうるう年になるのは2020年」「うるう年は4年ごと」という心優しい記述がありますが、受験生にとってはお馴染みの知識でしょう。
解答箇所イについても、「1年前の同じ日付の曜日はひとつ前の曜日になる。ただし、うるう年の2/29をまたぐときはふたつ前の曜日になる。」という、こちらもお馴染みの知識を使って処理します。
(3)
論理の問題。ゲームのトーナメントがテーマです。
解答箇所のアとイについては、このゲームのトーナメントの組み方にしたがって計算すれば答えを出すことができます。ただ、それだと解答箇所のウが苦しいでしょう。
このトーナメントのポイントは2つあります。
「1回のゲームにつき、負ける子どもが2人いる」
「最後まで負けないのは優勝者1人」
この2つのポイントを踏まえて考えてみましょう。
(ア) 81人のうち負けるのは優勝者以外の80人。
1回のゲームで2人負けるので、80÷2=40回ゲームが行われたことになります。
(イ) 235人のうち負けるのは優勝者以外の234人。
1回のゲームで2人負けるので、234÷2=117回ゲームが行われたことになります。
(ウ) 上記と同じ考え方でいきましょう。
(□-1)÷2=24回 という式が成り立つので、□=49人です。
(1)①②
平面図形と規則性の問題。
おうぎ形の紙をはり合わせていく問題です。後ほど詳述します。
(2)①②
図形の移動の問題。
2つの図形が平行移動ではなく垂直移動するという珍しいタイプの問題です。
設問①は16秒後の状態を正しく図示し、重なり部分の面積を求めるだけ。
設問②の解答箇所アイとウエは、図形の辺の長さと速さ次第ではとても面倒になる設問。しかし、今回は無理のない数値設定であり、解きやすくなっています。キリの良いところで確かめていくことで正答にたどりついた受験生が多く、それで問題ないと思います。
ただ折角なので、ここでは解答箇所アイについて、明確な処理方法を挙げておきます。
垂直移動で重なる時間帯を求めるときは、2つの図形の縦の幅、横の幅に注目し、通過算の考え方を利用します。
まず縦の幅ですが、台形の上底ADと下底BCは常に直線Xから上側に10cmの幅を保って移動します。この10cmの幅のところを正方形が通過するのは、4÷1=4秒後から、(4+10+10)÷1=24秒後まで。
次に横の幅ですが、正方形の縦の辺EFとHGは常に直線Yから右側へ10cmの幅を保って移動します。この10cmの幅のところを台形が通過するのは、8÷2=4秒後から、(8+10+20)÷2=19秒後まで。
よって、2つの時間帯で共通するところが答えになるので、4秒後から19秒後となります。
大問Ⅱまでが問題用紙1枚目で
大問Ⅲから問題用紙2枚目に入ります。
食塩水の問題。
色々なアプローチの仕方が考えられますが、どの解法をとったとしても所要時間に大きな差はつかないはず。易しい大問です。
唯一、設問(2)において、設問(1)で求めたA=200gを使うことに気づかなかった受験生がいたならば、そこで時間のロスにつながった可能性はあります。
時計算。 変則時計の問題です。
今年度の問題のうち、最も題意がとりにくかったといえるでしょう。
設問(1)の解答箇所アを求めることができなければ、大問まるまる落とすという恐ろしいことに。実際にそのようになった受験生が大半だった様子。ここで1問でも拾えた受験生は大きなアドバンテージを得たことになります。ただ、合格した受験生でも大問Ⅳは捨てたという声が多く、結果としては大問Ⅳを見切って、それ以外の問題に時間を割いて得点を積み重ねた受験生が賢明だったということでしょう。
合否を分けた一題
2019年度の算数は、従来の大問5つ構成から大問4つ構成に変わった2018年度を踏襲し、大問4つ構成。今後はこの形式が続きそうです。
特色は、2点挙げられます。
まず1点目は、題意が把握しにくい問題での足止め。
問題用紙1枚目左側の下に配置されたⅠ(3)トーナメントの問題と、問題用紙2枚目の最終大問Ⅳ変則時計の問題がこれにあたります。
どちらも通常のトーナメントや時計とは異なる“変則”的なものであるため、その内容の読み取りに時間がかかります。特に大問Ⅳは、時間をかけた挙句に、結局は理解できずに解けないままという危険性が高い問題です。その場合、どの程度の時間のロスで済んだかがカギになります。
2点目は、得点しやすい問題と得点しにくい問題の明白さ。
得点しにくい問題は、上記の題意が把握しにくいⅠ(3)、Ⅳに加えて、解答方針に迷いが生じやすいⅡ(1)①②。それら以外はほぼ得点しやすい問題です。
得点しやすい問題をミスなく確実に拾い切り、そのうえで得点しにくい問題においてどれだけ加点できたか。そこが合否の分かれ目だったといえます。
そこで、2019年度の合否を分けた一題として、上記の得点しにくい問題のうち、解答方針の選択と処理の精度がカギとなるⅡ(1)①②を取り上げます。
設問(1)①
おうぎ形A( 半径6cm、中心角19°)だけを、のりしろ部分の中心角を3°以上にしてはり合わせて円を作ります。
このとき、のりしろ部分の面積の合計が最も小さくなるのは、Aを何枚はり合わせたときかを考えましょう。
のりしろ部分の面積の合計をできるだけ小さくするためには、のりしろ部分の中心角をできるだけ小さくすればよいので、3°にします。
360÷(19-3)=22 あまり8 より、 Aを22+1=23枚 はり合わせたときです。
のりしろ部分の中心角の合計は 19×23-360=77°
よって、のりしろ部分の面積の合計は 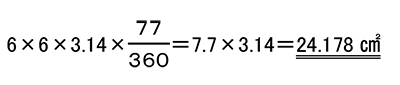
設問(1)②
おうぎ形Aとおうぎ形B(半径3cm、中心角19°)を交互に、のりしろ部分の中心角を3°以上にしてはり合わせて円を作ります。
このとき、のりしろ部分の面積の合計が最も小さくなるのは、AとBをそれぞれ何枚はり合わせたときかを考えましょう。
①で求めたように、おうぎ形が23枚のときになります。
ただし、この設問では「AとBが必ず交互になるように」はり合わせなければならないので、
AとBは同じ枚数、つまり合計の枚数は偶数となります。
よって、合計の枚数は23+1=24枚で、AとBはそれぞれ12枚ずつです。
このときできた図形の周の長さを、曲線部分と直線部分に分けて求めましょう。
◆曲線部分
A12枚の弧はすべて含まれるので
6×2×3.14×=7.6×3.14
B12枚の弧のうち、含まれるのはのりしろを除いた部分
のりしろ部分の中心角の合計は 19×24-360=96°なので
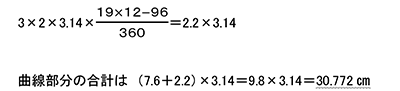
◆直線部分
AとAの間1つにつき 6-3=3cm が2か所できます。
AとAの間は全部で12個あるので
直線部分の合計は 3×2×12=72cm
よって、周りの長さは 曲線部分と直線部分を合わせて
30.772+72=102.772cm
桜蔭中入試対策・関連記事一覧
桜蔭中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から桜蔭中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
桜蔭中入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 理科の合否を分けた一題(2011年度)
- 理科の合否を分けた一題(2014年度)
- 理科の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)







