算数の合否を分けた一題
桜蔭中入試対策・算数の合否を分けた一題(2017年度)
難易度分類
| Ⅰ | (1)①A ②A (2)①A ②B ③B |
|---|---|
| Ⅱ | (1)A (2)A |
| Ⅲ | (1)①A ②A (2)A |
| Ⅳ | (1)①A ②A (2)A |
| Ⅴ | (1)A (2)B (3)B |
A:桜蔭合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題
問題別寸評
(1)①②
お決まりの順算・逆算の計算問題が1つずつ。
計算過程で出てくる数値の煩雑さは例年通りです。
(1)は最終的な答えの数値がシンプルで、一安心といったところでしょうか。
(2)①②③
場合の数の問題。
のちほど詳述します。
点の移動の問題。
2つの点が直方体の辺上を動く、出会いの問題です。
2点が出会うのは1つの辺上(辺DG上)に限定されることから、2点が辺の両端の点Dと点Gに着くのが何秒後かを調べ上げ、あとはキリの良いところから出会いの旅人算で処理するだけです。
調べ上げを伴うので、それなりの処理量を要しますが、この程度であれば確実に得点しなければならない問題です。
水そうとグラフの問題。
昨年の大問Ⅳも水量を追っていく問題でしたが、今年度の大問Ⅲはグラフの読み取りが必要なため、ひと手間かかる出題になっています。
ただ、その読み取りさえ誤らなければ、計算の分量は昨年よりも少なく、あっさり答えが求められます。
設問(1)①は、「容器Bの底面積(12☓12-3×3)☓与えられた容器Bの水面上昇率」で、おしまい。
設問(1)②は、①より3つの蛇口が毎秒5㎤ずつ水を入れることから、189秒間で入る水量を求めます。そこから容器Aと容器Bに入る水量をひき、残りの水量を容器Cの底面積でわって、おしまい。
設問(2)は、189秒かかったときと入れた水量の合計が変わらないという当たり前のことに注目すれば、時間の比と1つの蛇口から出る水量の比は逆比になることがわかります。
よって、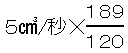 だけでおしまい。もたつくことなく短時間で処理できたでしょうか。
だけでおしまい。もたつくことなく短時間で処理できたでしょうか。
大問Ⅲまでが問題用紙1枚目。
大問Ⅳから問題用紙2枚目に入ります。
立体図形と不定方程式の問題。
設問(1)は、与えられた3つの立体の底面積と、それ以外の表面積を求める問題。
円周率計算をまとめたとしても、円周率計算の数値を覚えていたとしても、☓3.14の計算を複数回行うことになるので、ちょっと嫌気がさしてしまうかもしれません。我慢して計算しましょう。
ただし、鬱陶しい円周率計算を行うのは設問(1)だけ。
処理量を減らすために、設問(2)からは、赤36☓3.14、青18☓3.14、黄24☓3.14より、「赤36、青18、黄24」だけを用いて計算しましょう。
設問(2)は、上記「赤36、青18、黄24」の最小公倍数72より、赤・青・黄がそれぞれ72☓3.14になるときの白の合計を求めます。円周率計算をまとめると、1320☓3.14 になります。
設問(3)は、桜蔭算数頻出の不定方程式。受験生であれば練習を重ねてきたはず。数値が素直なので、計算過程で詰まるところはないでしょう。
立体1、2、3の個数をそれぞれA、B、Cとして式を作ると、「5☓A+4☓B+6☓C=60」となります。Aが偶数になることに気づけば、あとは問題文中の「立体1、2、3がどれも1個以上ある」「立体1、2、3はどれも異なる個数ある」という2つの条件を満たすような組み合わせを調べるだけ。
「解答らんは全部使うとは限りません」という但し書きも、いつも通りですね。
立体切断の問題。
大問まるまる切断として出題されたのは、H17大問Ⅵ、H22大問Ⅳ以来。そろそろ出題されるかな~と予想し、準備していた受験生も多かったのではないでしょうか。
設問(1)は何の変哲もない切断の問題。「小さい方の立体は三角すい」とまで、問題文で教えてくれています。
受験生なら誰もが知っている「展開図が正方形になる三角すい」になりますが、そこは問われておらず、大きい方の立体の体積が問われています。絶対に落とせない問題です。
設問(2)は設問(1)で求めた立体を利用するとラクに解けます。
設問(1)のときに、立方体アがどのように切られているか作図すると、三角すいが奥にできていることがわかります。この三角すいを設問(1)で求めた立体の体積からひけば、答えが求められます。
設問(3)も同様に、設問(1)で求めた立体を利用します。
設問(1)のときに、立方体イ、ウがそれぞれどのように切られているかを作図してみましょう。
立方体イは、三角すい台(Pとします)が奥にできています。そして、立方体ウは、立方体から三角すい台Pを取り除いた立体(Qとします)が奥にできています。
よって、PとQをたしたもの、つまり立方体1個分を、設問(1)で求めた立体の体積からひけば、答えが求められます。
独立した3つの設問ととらえるのではなく、設問どうしにつながりがあるととらえて解き進めることができれば、処理量を減らすことができた大問でした。
合否を分けた一題
2017年度の算数は、大問Ⅰ~Ⅴという構成に変化はありません。
ただ出題分野については、素材が立体図形に偏りすぎている感は否めません。細かく見れば桜蔭頻出分野の範疇におさまるものばかりではあるものの、大問Ⅱから最後の大問Ⅴまで、問題用紙に立体図形が与えられているのを見た受験生は戸惑ったのではないでしょうか。立体図形を得意とする受験生には有利なセットでした。
出題分野の偏りという点以外については
①難易度はけっして高くない
②どの問題もそれなりの手数を要する
③設問によっては解答方針により処理量に差がつく
という3点セットを満たす、例年通りの桜蔭算数だったといえるでしょう。
50分という限られた時間で、すべての設問を解き切るのは至難の業。
拾いにいく問題の取捨選択と時間配分、これがポイントです。
合否の分かれ目と考えられるのが、大問Ⅰ(2)①②③場合の数の問題。
冒頭の計算問題の直後に配置される、大問Ⅰの残りの問題は要注意です。数の性質、規則性、場合の数からの出題のときは、手数が多く、時間をとられる問題が多い傾向にあります。
今年度もそれに該当します。拾うなら3問とも確実に、とばすなら他の問題で得点する。
この3問にどう向き合ったかで、受験生の間で差がついたのではないでしょうか。
では、2017年度の合否を分けた一題として、その大問Ⅰ(2)を取り上げます。
Ⅰ(2)
計算で求める部分
書き出して調べる部分
この2つを明確に分けて解き進めるのがポイントです。
設問①
「10種の数字から2種を選ぶ」
⇒10☓9÷2=45通り の組合せがある
「2種の数字を4個並べる」
⇒並べ方は 2☓2☓2☓2=16通り
ただし、どちらも1回以上使うので、「AAAA」と「BBBB」の2通りを除いて
16-2=14通り
よって、45☓14=630通り
設問②
最も小さいのは、千の位に「0」を入れたとき
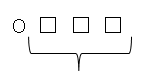
「0以外の数字の選び方」
⇒9通り
「2種の数字3個の並べ方」
⇒2☓2☓2=8通り
ただし、どちらも1回以上使うので、「000」の1通りを除いて
8-1=7通り
よって、0□□□のパターンは全部で
9☓7=63個
すると
0□□□ ・・・ 63個
1□□□ ・・・ 63個
2□□□ ・・・ 2000、2002、2020
63☓2+3=129番目
設問③
最も大きいのは、千の位に「9」を入れたとき
9□□□ ・・・ 63個
89□□ ・・・ 8999、8998、8989、8988 の4個
88□□ ・・・ □□の部分の8以外の数字の選び方
⇒9通り
□□の部分の数字の並べ方
⇒2☓2=4通り
ただし、どちらも1回以上使うので、「88」の1通りを除いて
4-1=3通り
よって、9☓3=27通り
ここまでで、63+4+27=94個
求めるのは92番目の数なので
94番目 8800
93番目 88.08
92番目 8811
桜蔭中入試対策・関連記事一覧
桜蔭中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から桜蔭中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
桜蔭中入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 理科の合否を分けた一題(2011年度)
- 理科の合否を分けた一題(2014年度)
- 理科の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)








