算数の合否を分けた一題
桜蔭中入試対策・算数の合否を分けた一題(2010年度)
平成21年
1科目50分になってからの桜蔭中の算数は、以前と比べて確実に点数が取り易くなっています。たしかに問題の傾向そのものの変化は少ないのですが、調べ上げる手間が格段に少なくなっているのです。
したがって正しい桜蔭中対策をした生徒にとって、7割が合否のボーダーラインになっていると推定されます。かなりの高得点勝負と言え、ミスが許されない、まさに女子最高峰の試験と言えるでしょう。
平成21年の算数も、例年の傾向に沿った出題でした。ただ、この年は、問題の難易度そのものは抑え気味であったものの、計算の分量が多く、桜蔭対策の質と量によって、大きな得点差が出たものと思われます。
出題別難易度
1 AAB ABB
2 AA
3 BB
4 ABC
5 AAAB
A…桜蔭中合格を目指すなら確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題
5
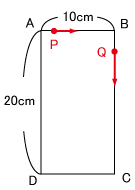
右の図のように、たて20cm、横10cmの長方形ABCDがあります。
この長方形の辺上を、点Pは点Aを出発して
A→B→C→D→A→・・・・・・の順に、
点Qは点Pと同時に点Bを出発して、
B→C→D→A→B→・・・・・・の順に動きます。
最初の1周は、点Pは毎秒1cm、点Qは毎秒2cmの速さで動きます。その後、点Pは2周目は毎秒2cm、3周目は毎秒3cm、・・・・・・・、点Qは2周目は毎秒3cm、3周目は毎秒4cm、・・・・・・のように、どちらの点も1周ごとに秒速を1cmずつ増やしながら動きます。
(1)点Qが点Pに初めて重なるのは、出発してから何秒後ですか。
(2)1周目から3周目までについて、2点P、Qがそれぞれ長方形ABCDを1周するのにかかる時間を下の表に書き入れなさい。ただし、単位は秒としなさい。
(3)出発してから100秒後に2点P、Qはどこにいますか。下の(例)のように図1に点P、図2に点Qの位置を書き入れなさい。考え方も書きなさい。
(例)点Pが100秒後に辺AD上のAから7cmのところにいるとき
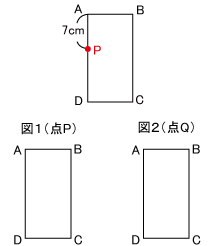
図2
(4)出発してから100秒間の間で、点Qが点Pと最後に重なるのは出発してから何秒後ですか。

図3
点の移動と呼ばれる、一般的な旅人算で、問題の誘導に乗って表で整理することができれば決して難しくはないのです。
ただ、どうしてこの問題が合否を分けたのか。その理由は「問題の配置」と「答えの数字の汚さ」にあります。
この年は例年に増して計算量が多く、最後の問題である5に、どれだけの時間を残すことができたかが勝負を分けました。もし時間配分に失敗し、5分程度しか考える時間が残されなかったのならば「方針は分かっているのに間に合わない」という事態におちいってしまうことが想定されます。
また(3)(4)の答えが複雑な分数になることも、受験生としては不安を駆られることでしょう。しかし、桜蔭中の対策を十分にこなして着ていれば、汚い数字になることには慣れているはずです。
桜蔭中で注意したい「時間配分」と「大胆さ」が身についているかどうかで、まさに合否を分けた一題と言えるのではないでしょうか。
桜蔭中入試対策・関連記事一覧
桜蔭中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から桜蔭中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
桜蔭中入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 理科の合否を分けた一題(2011年度)
- 理科の合否を分けた一題(2014年度)
- 理科の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)







