算数の合否を分けた一題
武蔵中入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| 1 | (1) A (2) A |
|---|---|
| 2 | (1) A (2) A |
| 3 | (1) A (2) B (3) B |
| 4 | (1) A (2)ア B イC ウ B |
A…武蔵中合格を目指すなら確実に得点したい問題
B…知識、解法次第で得点に大きく差がつく問題
C…難度、処理量から判断して得点差がつかない問題
2021年度 出題総評
合格者平均/満点 = 58.4点/100点
受験者平均/満点 = 42.0点/100点
2016年以降、隔年的に点数が上下しており、今年は点数が低い年となっています。難度が上に振れても下に振れても対応できる力を養成しましょう。
問題別寸評
正確に作業できれば何とかなるでしょう。
後半の3.4.で大きく差がついたと考えられます。
与えられた線分比の使い道がわからないと(1)止まり、
逆に(2)をクリアできていれば(3)はほぼ取れるので、点差が大きく開きます。
(2)の調べのうち(イ)で全ての場合(10個)を求めさせて、そのうちの一部が(ア)と(ウ)の答えになるという作りでした。一般的には(ウ)が2番目に配置されそうなものですが、受験生はどう動いたでしょうか。(ウ)の前に(イ)に着手すると、両方失う危険があります。
賢明に(ウ)から手を出せば、(イ)を落としても2問は拾えるので、全体を見て易しい順に着手できたかどうかで差がついていると考えられます。
大問3と大問4のうち、どちらかで得点を稼げば、合格ラインは超えられるでしょう。
【2021年度 問題別寸評】
(2) 仕事算
(ア)
ポンプA、Bが同じ水量を注ぐのにかかる時間の比は
A B
時間 2.1 : 1
故障したBが入れそこなった水を、Aが予定の時間の後42分かけて補充した
と考えてみましょう。
Bが止まっていた時間を□とすると、求めた時間比を用いて
42:□ = 2.1:1
これより□=20分とわかります。Bが故障しなかった場合、水槽を満たすのに
32+20=52分かかります。
(イ)
注水速度の比を求めます。
A B
時間 2.1 : 1
↓逆比
注水速度 10 : 21
AとBが52分で注水する量:Bが1分で注水する量
=(10+21)×52 : 21×1
= 1612 : 21
これより、
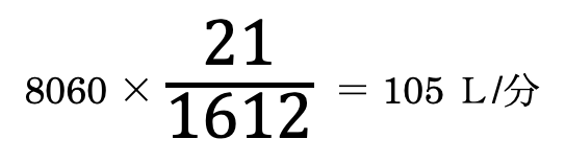
と求めることができました。
なお問題文に「Bが故障するまでの間、Bが入れた水」とあるので、1分当たりの水量でなく入れた水の合計を答えた人が少なからずいた可能性があります。
2人が山越えの道を反対方向に動きます。山はありますが問題として超えるべき壁がないので、この問題は絶対に得点する必要があります。
とにかく条件を書き出して、図を書いて、丁寧に作業していくことです。
(1)
実際に歩いた時間は、
A…285分
B…265分
ここからは典型題です。
・P-山頂間と、山頂-Q間で時間比2:3を用いて消去算の式を立てる
・P-山頂間と、山頂-Q間の長さの差の部分に注目する
のいずれかの方法で情報をまとめます。
差の部分に注目すると、下のように時間を整理できます。(図1)
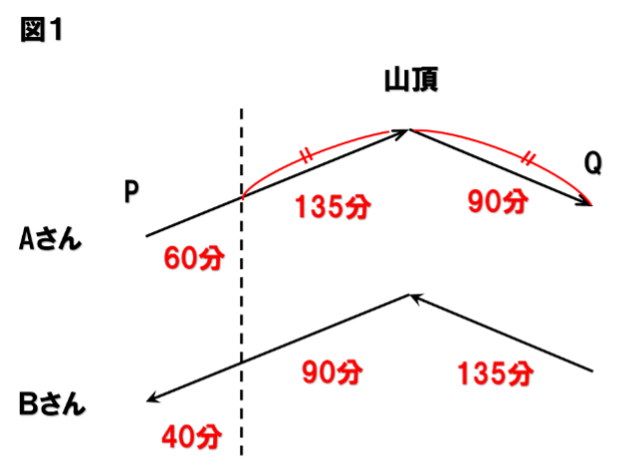
これで3つの区間の長さの比が4:9:9とわかります。(図2)
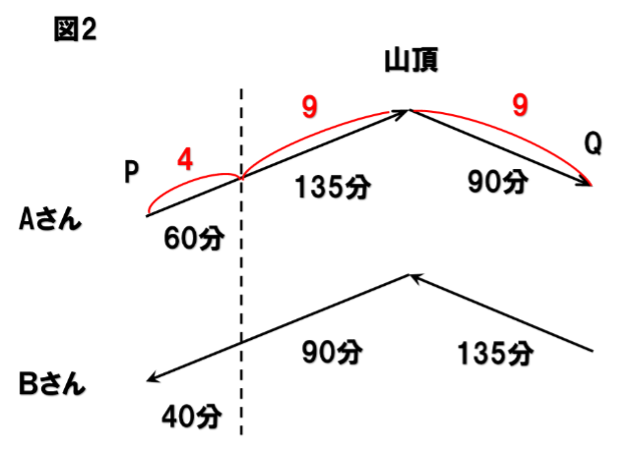
ここまでくれば(2)(3)は答えが出ます。
(4)
Bさんは山頂を12:45に出発して、Pに14:55に着きました。
BさんとCさんの動きをダイヤグラムに表して出会った時刻を求めてみます。
まず上記の情報を表します。
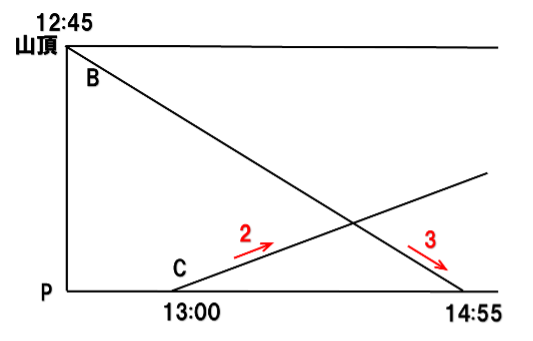
ここで上りの速さ:下りの速さ=2:3を用いると、時間の比は逆比になるので、次のようになります。
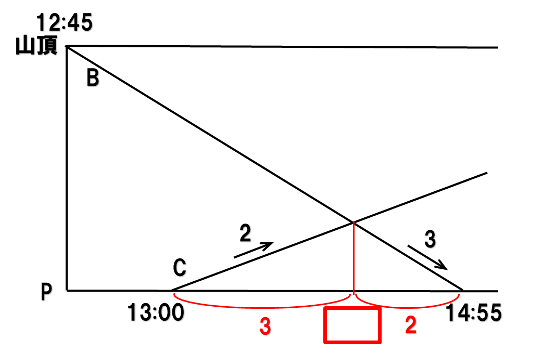
これで、出会った時刻=14:09と求めることができます。
「合否を分けた一題」で後述します。
(1)
立方体の展開図になっている図を選びます。ここでは差はつかないでしょう。
(2)
「ルール」を満たす展開図の個数を数えます。
向かい合う3組の面のうち、2組の面は書かれた数の和が12である
アとウはその場で思いつけば正解に至りますが、イでは「全て」を求めなければなりません。したがって、何となくやっているうちにできてしまうことはありません。
全部を調べきるためには、全ての場合を考えて、それぞれを調べることを考えます。
まず和=12となる2つの数は、
1,11
2,10
3,9
4,8
5,7
に限られます。
このうち4と8は隣接しているため、向かい合わせることは不可。
あ1,11
い2,10
う3,9
え5,7
の4通りです。この4つのうち、2組が向かい合う場合
あい、あう、あえ、いう、いえ、うえ の6通り(※)をすべてチェックすれば、念願達成です。
説明のために あ、い、う、えの4ペアを等しい色で表してみました。(図1)
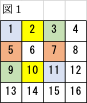
あ1,11とい2,10のペアが向かい合う場合を考えます。
下の図2で、色を付けた2組が向かい合う展開図は何通り作ることができるでしょうか。
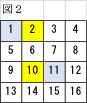
まず6を使って2と10を向かい合わせるので、ここまで決まります。(図3)
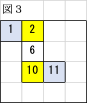
次にこの5枚の面を組み立てて、残る1面を決めましょう。6と向き合えるのは〇印を付けた14,15の2か所ということになりますね。
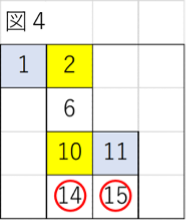
これで(1,2,6,10,11,14)と(1,2,6,10,11,15)の2例が出ました。以下、同様に進めることですべての個数を数えることができます。
さて、この段階で(1,2,6,10,11,15)が設問ウの答えになっていることがほぼ確定します。
図1を見ると、16を使った展開図はルールを満たさないことがわかりますね。
そして、2例が決まったということはあと1例挙げれば設問アが終了します。
もし最初から狙ってイを取りに行けば、アとウをやる必要はほぼありませんね。
ただ、実際に最初からこのようにできるかというと、設問アで探索しているうちにルールになじみながら運用し、最後に全部の場合を調べきる、というのが大半の受験生の動きだったと考えられます。一般にルールの問題は、読めばすぐわかる類のものではなく、読んで意味を考え、作業をしてルールを正確につかむところまで時間がかかるのです。それゆえ、解の一部を答えさせる設問で点数を与えているとも言えます。
ここではアとウで正解できていれば、合格ラインを超える可能性が高いと思います。
全ての場合を調べるために重要なことは、何に着目して場合分けするのか、ということです。ここでセンス(=練習で培われた動き)の差が顕著に出ます。
どうやったらすっきり場合分けできるか、常に悩みながら勉強することで、このセンスは磨かれます。
解説中に示した
のように全体を場合分けできれば、イからアタックするチャンスもでてきます。
合否を分けた1題
3.平面図形
正六角形の面積比問題です。
(1)
全く差がつかないでしょう。合否に影響なしです。
(2)
最初の条件を図に表します。(図1)
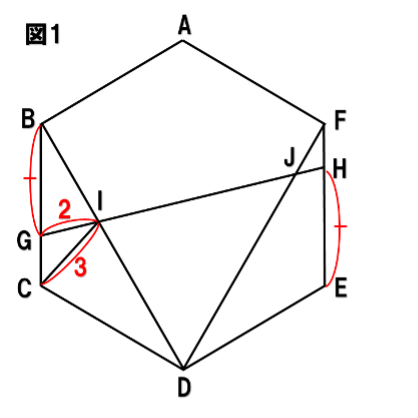
与えられた条件
GI:IC=2:3
をどう使うかを考えます。
このままの状態では身動きが取れません。
BG=EHからGHが六角形の「中心」を通ることに注意して、補助線を引いてみます(図2)。
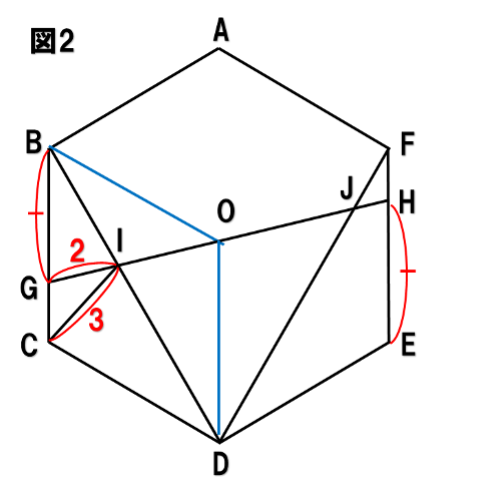
すると、どうでしょう。
ひし形OBCDは対角線BDに関して線対称になっています。これを利用して
IC=IO
となり、GI:IO=2:3が決まります。(図3)
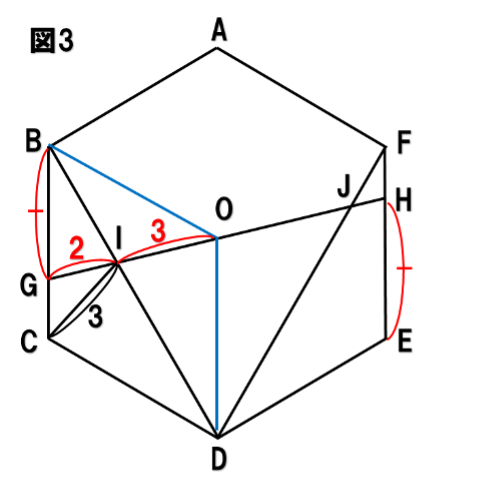
ここまでくると、ゴールが見えてきます。
△BGIと△DOIは2:3の相似になっていることを利用します。(図4)
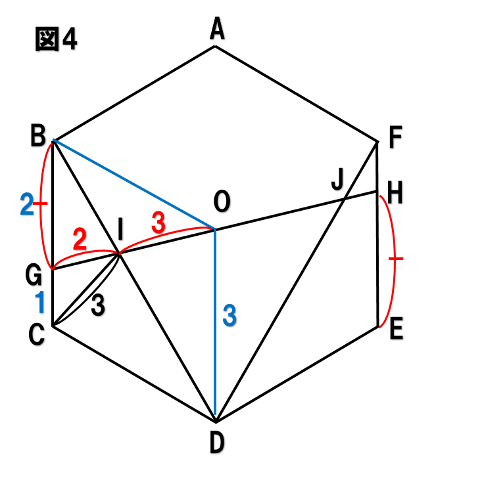
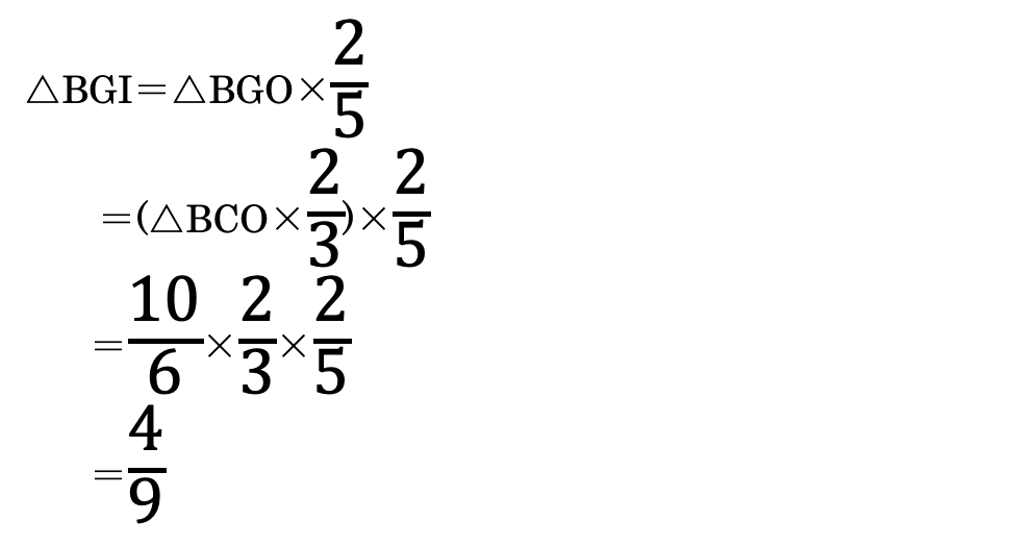
となります。
(3)
(2)でBI:ID=2:3がわかっています。
△BDFは正三角形です。これに注目すると、図5のように見えてくるはずです。
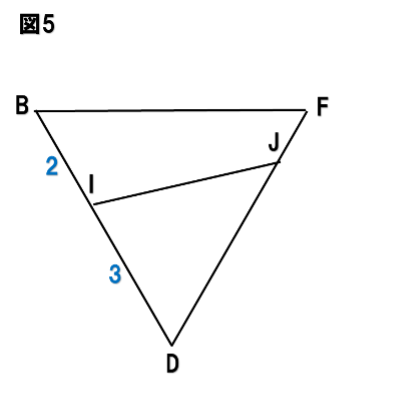
あとは△ODJと△HFJの相似からDJ:JF=3:1が出るので、これで余裕をもって△IDJの面積が出せるでしょう。
(2)で上手く動けたかどうかで合否が分かれたと言ってよさそうです。
図1の状態で手が止まり、いろいろ画策して、うまく這い上がって行けたかどうか…
(2)がすんなりできた受験生はここで3問正解となり、高い確率で合格しているものと思います。
武蔵中入試対策・関連記事一覧
武蔵中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2011年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から武蔵中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
武蔵中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)