算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

武蔵中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

１	(１) アA　イA　ウA　エB　(２) A
２	(１) B　(２) B　(３) B
３	(１) A　(２) B　(３) C
４	(１) A　(２) アB　イB　(３) アB　　イ C

A…武蔵中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題

2019年度　出題総評

合格者平均／満点＝　55.2点／100点
受験者平均／満点　＝　39.4点／100点
武蔵の算数としては、例年より点数の取りにくい問題でした。
上記難易度分類のCレベルでは点差がつかず、できるところを確実に取ることが合格につながったと考えてよさそうです。

全体としては、確実な作業力が問われる問題構成でした。

問題別寸評

１数の性質

（１）

ア、イ
漏れのないよう、慎重に書き出しましょう。
ウ、エ
約数の個数、約数の和は素因数分解を利用して求める方法を知っておくと早く確実にできます。約数の和はエで必要となります。
約数の「逆数の総和」ですが、定番問題です。2018年海城中（１回）の大問3で出題例が見られます。
160の逆数の和にその数自身＝160をかけたものを考えると、「約数の和」になるということを確実に押さえておきたいところです。
これを知らない受験生にとっては簡単ではなかったと思われます。その場合は、時間がかかりそうだと踏んで回避するのが得策でしょう。

(２)

　
1から10000までの整数について、
31の倍数の個数
31×31の倍数の個数
…
と順に調べていきます。落とせない問題でした。

２　平面図形

→【合否を分けた１題】で後述します。

３　点の移動

P、Qの出発時刻が5秒差であることに注意しながら進めます。

(１)

まず1回目を考えます。
BP=15㎝の状態から、２点が動き始めます。つまり
15㎝の出会い算になります。

次に、２回目を考えます。
今度はPがQに追いつくときです。
15㎝の追いつき算です。

「点Pが動き始めてから」とあるので、最初の5秒を足し忘れないよう注意してください。

(２)

（１）の１回目と２回目に平行四辺形になった時の上底+下底は、
１回目　 6×2＝12㎝
２回目　30×2＝60㎝
なので、これを比べれば高さを求める必要はありません。上底+下底が5倍なので、面積は
75を5倍して、375㎠と求まります。

（３）

上底+下底＝BP+CQ の最小値と、最小となる時刻を求めます。
2の長さはそれぞれ異なる変化をするので、和を追いかけるのは容易ではありません。
思い切ってグラフを書いてみるとよいでしょう。
①BPのグラフ
②CQのグラフ
③BP+CQのグラフ
の順です。

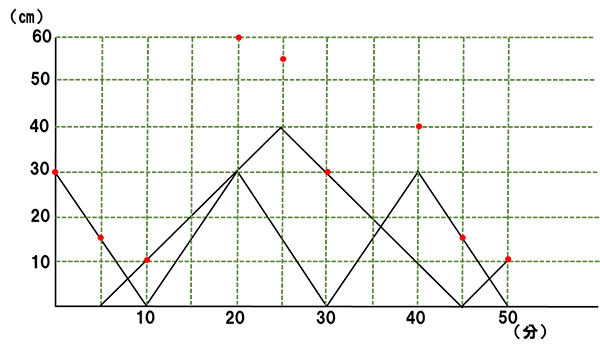
まず、①BPのグラフと②CQのグラフをかくと、以下のようになります。

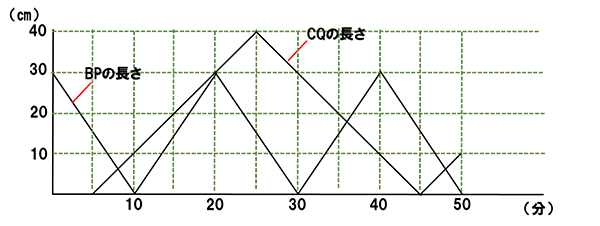
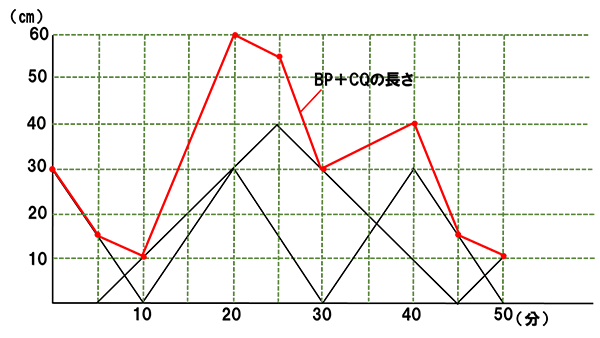
次に、③BP+CQのグラフをかきます。
各時刻におけるBP+CQの値を追いかけていけばよいのですが、書き方のポイントは以下の通りです。
（１）変化の仕方が変わる点（グラフの折れている箇所）を押さえる
（２）一方の値が0の時、もう一方の値がBP+CQの値となる
（３）①と②の2つのグラフの交点でBPとCQが等しくなるので、和のグラフはその交点の値を2倍する

上記の（１）と（３）を使ってBP+CQの値を点で打つととこうなります。

お互いの変化の仕方が変わらない区間では、和も一定の変化をするのでグラフは直線となります。すなわち、打った点を直線で結べばBP+CQのグラフが完成します。

グラフから、上底+下底＝BP+CQ の最小値は
BP+CQ＝10㎝、
最小となる時刻はPが出発してから10分後とわかりますので、
その時の台形アの面積は、

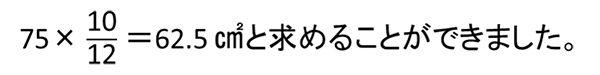
ところで、このグラフを利用するとBPとCQのグラフの共有点が（１）の答えを示していることがわかります。初めからそれを見越してグラフで攻略すれば、短時間で全問得点できるチャンスもあります。
ただ、そこまでしなくても得点可能な（１）（２）を確保して、（３）は敬遠するのが順当なところと言えそうです。
なお2量の和の変化を追う出題例が2005年駒場東邦の大問3で見られます。このようなグラフを練習しておくと、他の受験生に差をつけることができるでしょう。

４　場合の数、調べ上げ問題

与えられたルールに従って操作を行い、調べていきます。どういう手順で数え上げるか、要領を得ないまま取り掛かってもうまくは行きそうにありません。

（１）

色の塗られていない（＝白い）ますは１箇所。これが1列目から6列目にくるときのまわりの長さを調べればわかります。

（２）ア

今度は白います＝3箇所が条件。各列の白いますの個数はルールより1または2ですから、1列目から6列目における白いますの個数が
2,1,0,0,0,0
1,1,1,0,0,0
の２つのパターンについて配列の仕方を調べれば、まわりの長さがとる値をすべて求めることができます。

（２）イ

前の問題でまわりの長さ＝24㎝となるパターンを1つ求めているはずです。たとえばそれが
0,1,0,2,0,0
であったとします。深さ1と深さ2の穴が
・隣り合わない
・端の列（1列目、6列目）に来ない
と言う条件を満たす配列を考えればよいので、条件を言い換えると
「0,0,0,0の3か所のすき間のうち、異なる2箇所に1と2を配置する」の場合の数に等しくなります。1の場所、2の場所を考えて
3×2＝6　通りとなります。

（３）ア

まわりの長さ＝26㎝はすぐわかるので、比較的容易に調べることができます。

（３）イ

前問に引きずられて、面積＝13のときがあることを忘れないように注意してください。
面積＝12のとき、0,0,0,2,2,2
面積＝13のとき、0,0,0,1,2,2
面積＝14のとき、0,0,0,0,2,2
の配列を、まわりの長さ＝26㎝を損なわない範囲で調べます。
終わりが見えず手強い作業になりますが、この設問で差がつくことはないでしょう。

合否を分けた１題】

大問２を取り上げます。

2018年の大問２の電車の問題でもそうでしたが、
全問正解か、全問不正解か
で大きな得点差がついてしまう問題であったと考えられます。

まず等しい角度を表す記号を、角DEFの錯角である角BFEにもつけてみます。

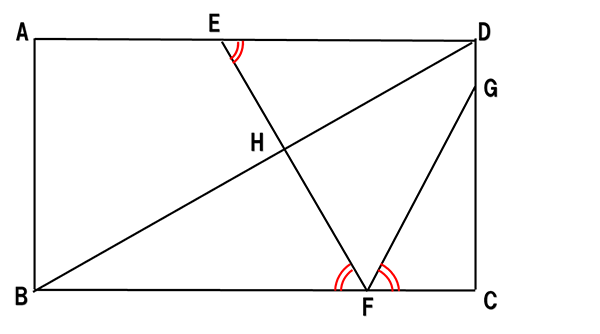
これで、下の図のような直角三角形の相似が見えてきました。

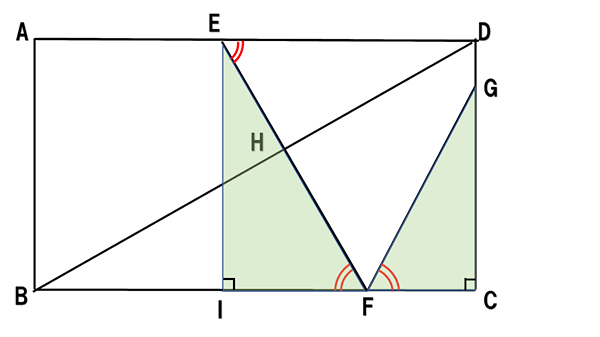
図のようにIをおきます。DG:GC=2：5から、相似比7：5もわかりますね。

（１）IC=8㎝を7：5に分けて終了です。
（２）三角形GFCの面積と底辺FCから、高さGCを求めることができます。
（３）三角形EHDと三角形FHBの相似比＝3：4から、長方形の高さに対する三角形BHFの高さの割合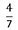＝がわかるので、三角形GFCと直接比較してみます。

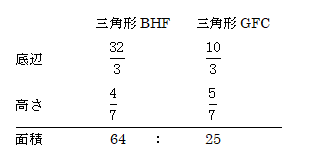
これを用いて、三角形BHF=25.6を求めます。
図をよく見ると、反射の問題に似ています。反射の問題では入射角=反射角の関係を利用して、相似な直角三角形を考えていくのは定石と言えるでしょう。
図を見て反射的に相似が見えればすんなり終わる問題構成ですが、見えなければ全問外しの危険のある問題でした。