算数の合否を分けた一題
武蔵中入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| 1 | (1)A (2)三角形AEG・・・A 台形ABCE・・・A |
|---|---|
| 2 | (1)A (2)B |
| 3 | (1)B (2)B (3)B |
| 4 | (1)A (2)A (3) <図5>A <図6>B <図7>B |
A…武蔵中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
問題別寸評
(1)
中学受験生にとって、基本的な数の性質の問題です。確実に正解しなくてはなりません。
(2)
辺ADと辺BCにおいて、AE:ED=24:16、BF:FC=15:25と比をそろえ、相似形・面積比を活用すれば正解できるでしょう。武蔵中学の過去問などで十分な準備をした受験生にとっては、拍子抜けするようなレベルでした。合格するためには落とせない問題です。
(1)
基本的な食塩水の問題です。確実に正解しなくてはなりません。
(2)
武蔵中学受験生であれば、必ず解いた経験のある食塩水を移し替えていく問題ですが、最終的にAとCの量が異なるなど、いざ解き始めると手が止まってしまった受験生も多かったと思います。
この問題では、濃度の変化ではなく、含まれる食塩の量で考えると良いでしょう。
Aに移す前のC500gに食塩が⑤含まれているとすると、最後のA400gには食塩が15+①g、C500gには食塩が④+0.6g含まれています。
A400gとC500gは同じ濃度より、それぞれに溶けている食塩の量を考えてみると、(15+①):(④+0.6)=4:5が成り立ちます。
ここをうまく処理できたかどうかで差がついた問題でしょう。
(1)
こちらも武蔵中学受験生であれば、必ず解いた経験のある旅人算です。
ただし、同乗者がいるときといないときの自動車の速さが異なる点が難しいです。
女子がA地点まで3÷4.5×60=40分かかり、自動車は3÷45×60=4分かかるので、自動車がAB間の往復に40−4−1=35分とわかります。
あとは、45㎞と60㎞から速さと時間の逆比の利用で、正解を導くことができでます。
(2)
(1)で、学校からB地点まで24分、B地点からA地点まで15分とわかっており、A地点を出発してから男子に追いつくまで24分とわかります。
(3)
追いついたところから終着地点までに注目して、速さと時間の逆比を利用する、武蔵中学の頻出問題です。
(1)をクリアすると(2)と(3)は解ける問題です。(1)の出来が得点を大きく左右したといえます。
(1)
題意の確認問題です。確実に正解しましょう。
(2)
6点を多く作ることを考えます。斜めに×を入れると、6点が2ヶ所作れます。
(3)
<図5>4点を作る方法は、2個で3点、1個で1点、4個で0点を作ります。
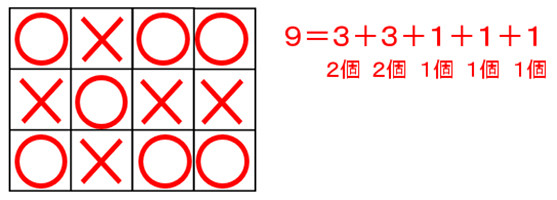
<図6>3点×3=9点とすると、残り1個で1点加わり合計10点となってしまいますので、2個で3点を2ヶ所、1個で1点を3ヶ所作ります。
<図7>3個で6点、2個で3点、1個で1点を2ヶ所で11点を作ることは、すぐに思いつくでしょう。3個をどのように入れるかがポイントになります。
合否を分けた一題
2016年度の武蔵中学の入学試験問題は、例年通り大問4題構成で、大問1が数の性質と平面図形、大問2が食塩水の交換、大問3が旅人算、大問4が場合の数と、武蔵中学の典型的な出題構成でした。
武蔵中学の算数は、年度によって難易度にばらつきがあるといわれますが、数の性質・平面図形・和差に関する問題、割合に関する問題、速さ、場合の数から多く出題されています。
その中で標準レベルから応用レベルの間で出題されており、10年以上の長い期間で見ると出題レベルは一貫しているのですが、年度によって難しい問題が集中する、あるいは易しい問題が集中するケースがみられます。
今年度は易しい問題中心の構成で、受験生からも「簡単だった。これでは算数で差がつかない」という意見が多かったです。
確かに、大問1は確かに易しかったと思いますが、大問2の(2)、大問3は易しい問題ではありません。そこで受験生の反応と合わせて考えると、このレベルの問題が解けるかどうかが、最初の合否の分かれ道だったといえます。
武蔵中学を目指す受験生にとっては、試金石となる問題として活用できるでしょう。
その中で、合否を分けた一題として、大問4を取り上げます。
(1)題意の確認問題です。確実に正解しましょう。
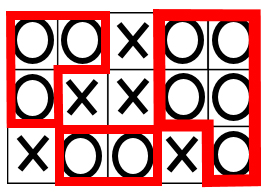
よって、6+3+0=9点となります。
(2)

斜めに×を入れると、6点が2ヶ所作れます。
(3)
<図5> 4点は、2個で3点、1個で1点、4個で0点を作ります。
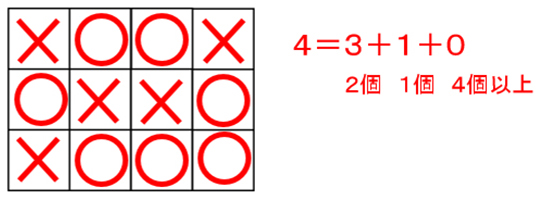
<図6> 3点×3=9点とすると、残り1個で1点加わり合計10点となってしまいますので、2個で3点を2ヶ所、1個で1点を3ヶ所作ります。
<図7> 3個で6点、2個で3点、1個で1点を2ヶ所で11点を作ることは、すぐに思いつくでしょう。3個をどのように入れるかが頭を悩ませる点です。
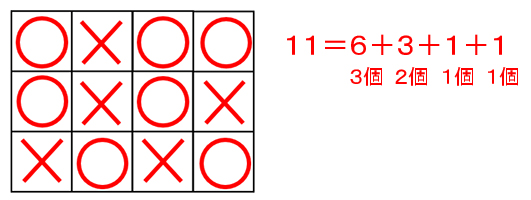
3個をたてや横に一列で並べようとすると、上手く入れることができません。
上の図のように入れることがポイントとなります。
決して難しい問題ではありませんが、例年の調べ上げていく問題と異なり、部分点がなく正解か不正解のどちらかになります。<図6><図7>を上手く見つけられたかどうかが、得点を大きく左右した問題であったと思われます。
武蔵中入試対策・関連記事一覧
武蔵中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2011年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から武蔵中学入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
武蔵中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)