理科の合否を分けた一題（2016年度）

難易度分類

［１］	問１Ａ　　問２Ａ　　問３Ｂ　　問４Ｂ
［２］	問１アＡ　　イＡ　　ウＢ　　エＡ　　オＢ問２Ｂ　　問３Ａ　　問４Ｂ　　問５Ｂ　　問６Ｂ
［３］	問１Ａ　　問２Ａ　　問３Ｂ　　問４Ａ　　問５Ｃ（方法１・２とも）

A…武蔵中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

大問は物理・生物・地学の各分野から１題ずつの計３題、小問にすると20題でした。
学校が公開している情報によると、今回の平均点（60点満点中）は、合格者平均39.1点（183人）、受験者平均34.3点（590人）でした。
問題のレベルだけを考えれば、もう少し平均点が高くても良さそうなものなのですが、合格者平均でも約65％しかいかないということは、それだけ時間に追われて間違えてしまった受験生が多かったということでしょう。
問題数そのものは決して多いわけではありませんから、途中の考え方や式を書く問題、説明記述の問題などで、いかに要点をしぼって書けるかが明暗を分けた可能性もあります。

問題別寸評

１

クレーンを題材とした、てこのつり合いに関する問題です。図の雰囲気に惑わされることなく、支点・力点・作用点がそれぞれどこになるのかを意識しながら解く必要があります。

問１

棒の重さを無視してよい問題ですから、てこの計算としては簡単なものでしょう。
言うまでもなく、Ａが作用点、Ｂが支点、Ｃが力点を表しています。

問２

落ち着いて取り組めば何も難しくない問題ですが、テストが始まった直後に取り組んでいる受験生が多いことを考えると、あわててミスをしてしまった人も少なからずいるでしょう。
問題文に、「図２では腕が斜めに延びていますがＡＢの間隔は図１と同じなので、バランスのとり方も図１と同じと考えることができます」という説明がある通り、重要なのは水平方向の距離ですので、「腕の長さが10m」という条件は使いません。
ＡＢとＢＣの間隔の長さの逆比から、ちょうどつり合う重さを求め、「ちょうどつり合う物の半分の重さまでしかつり上げてはいけない」という条件にしたがって、求めた重さを半分にして答えます。最後まで気を抜かずに答えを出しましょう。

問３

問題文で例示された図３を、正しく理解することができたでしょうか？
Ａは作用点の位置、Ｂは支点の位置、Ｃは力点の位置を表しています。つまり、クレーン車全体を一つのてこと考えるのなら、Ｂの線が引いてある位置は、クレーンの腕の付け根ではなく、クレーン車を支えているタイヤの位置なのです。
これが見破れていれば、この問３でも迷わずに、左側のタイヤの位置に線を引けるでしょう。しかし、勘違いしてうでの付け根の部分に線を引いてしまった受験生が多いのではないかと予測します。

問４

問３で正しくＢの位置を考えることができた人は、図５でのＢの位置が、車体の横に張り出した支えの位置になることも理解できたでしょう。そこさえクリアできれば、計算自体は難しくありません。
詳細な計算は、最後に「合否を分けた一題」として解説します。

２

よほど好きな人でもなければ、クモの網（巣）の張り方なんて知らないでしょうから、いかに正しく説明の文章を読めるかが鍵となります。
一方で、昆虫に近いなかまとして、クモ類や甲殻類、多足類については、ある程度知っておいてほしいと思います。
また、節足動物以外の無セキツイ動物についても、軟体動物（タコ・イカ・貝のなかま）くらいまでは押さえておきたいところです。

問１

昆虫類については細かく学習している受験生が多いことと思いますが、昆虫に近いなかま（節足動物）の特徴について、どこまで深い知識を持っているかが問われる問題です。

【ア】
節足動物としての一番大きな特徴ですから、合格のためには、ここはきちんと正解してほしい問題です。

【イ】
昆虫の脚が６本であることはほとんどの受験生が覚えているでしょうから、クモの脚が８本（４対）であることを知っているかどうかです。ただし、これも基本中の基本でしょう。

【ウ】
「考えたこともなかった」という受験生が多いかもしれません。セキツイ動物を内骨格と呼ぶのに対して、節足動物は外骨格と呼ばれ、体の外側に骨格を持っています。したがって、体を大きくするためには、どうしても脱皮をする必要があるのです。したがって、脱皮は、甲殻類なども含めたすべての節足動物に共通する特徴なのです。

【エ】
ぜひ正解してほしい問題なのですが、実際にはきちんと覚えられていない受験生も相当数いたのではないかと思います。昆虫類は頭部・胸部・腹部の３つの部分に分かれていますが、クモ類は頭胸部・腹部の２つにしか分かれていません。ちなみに、甲殻類も頭胸部と腹部の２つに、多足類は頭部と胴部の２つに分かれています。

【オ】
昆虫類の中でも、完全変態の昆虫にしかさなぎの時期がないことは、すぐに思い出せたかと思います。問題は、クモ類をどのように考えたかでしょう。節足動物の中でも、最も進化しているのが昆虫類ですが、昆虫類の中でも、特に進化した存在が完全変態の昆虫なのです。その完全変態の昆虫にしかないさなぎの時期ですから、当然クモ類にはありません。クモ類に属するほとんどの生物は無変態です。

問２

あまり多くかけすぎると切れてしまいますが、霧吹きで細かい水滴をつけると、クモの網は観察しやすくなります。小中学生向けの実験観察の手引きなどでも、クモの網を観察するときには霧吹きを使うことが推奨されています。
また、背景が暗い場所や黒い紙の前では、懐中電灯の光をクモの網にあてるとキラキラ輝いて観察しやすくなります。実際に、クモの網を標本にする場合などにも、背景に黒い紙を置き、クモの網だけに光をあてる方法が使われることがあります。
上記からも分かるように、クモの網は白っぽいので、クモの網自体を光らせる工夫が有効です。白い粉や白い紙では逆効果でしょう。また、うちわであおぐと、光のあたり方に変化が起こるために見やすくなる可能性はありますが、観察実験において対象物を動かすのはあまり良い方法ではありません。
余談ですが、これは実体験の差がはっきりと出る問題かもしれません。雑木林などの自然の中でよく遊んでいた子どもであれば、雨上がりの日にキラキラと輝くクモの網の美しさに息をのんだ経験もあるのではないでしょうか。

問３

これは理科というより国語の問題です。文章がちゃんと読めていれば、何も難しくありません。武蔵中に合格するためには、これは絶対に得点しておきたい問題です。

問４

ちゃんと文章を読んでいれば、おそらくタテ糸までは問題なくかけるでしょう。読み方で差が出るのは、きっと「足場糸の有無」と「ヨコ糸のかき方」だと思います。
まず、足場糸については、文章中で「回収しながら」と説明されていますので、完成したクモの網には足場糸は残っていません。したがって、二重線でヨコ糸をかくと不正解です。
また、ヨコ糸を張るときには、「こしき」から渦巻き状に張った足場糸を逆にたどりながら張るのですから。ヨコ糸も渦巻き状になるはずです。したがって、同心円状にかいたら不正解となります。

問５

易しい問題なのですが、難しく考えすぎて間違えてしまった人もいるかもしれません。
この問題のポイントは、「確実にわかること」という一言です。なぜヨコ糸を避けているのか……と考え始めてしまうと、「伸び縮みしやすい糸だから歩きにくいのではないか」とか、「粘着性があると書いてあったからクモ自身もくっついてしまうのではないか」などと考えてしまうと思いますが、それらはすべて「考えられること」であって、「確実にわかること」ではないのです。
この観察結果（問題文）から確実にわかることは、「クモはヨコ糸とタテ糸を区別している」ということだけです。

問６

足場糸と同じ位置に、わざわざヨコ糸を張り直すわけですから、それはヨコ糸の特性を活かすためだと考えるのが自然です。そして、ヨコ糸については、「伸び縮みしやすく粘着性のある」という説明がされていますから、これが虫を捕らえるのに役立っているということです。
ここで、粘着性があるという特徴が虫をくっつけるのに役立っていることは容易に想像がつくでしょう。難しいのは伸び縮みする特徴の方だと思いますが、これは、虫が網にかかった時に切れにくくなることで役立っています。
問題の指示にしたがって、特徴と役割を関連させながら解答しましょう。

３

入試問題に詳しい人であれば、武蔵の理科と聞けば、毎年恒例の「袋の問題」を連想することでしょう。
武蔵中学では、2015年は「転写紙」、2014年は「分離した２種類の液体が入った容器」、2013年は「３種類の電気ケーブル」、2012年は「曲がるストロー」、2011年は「発光ダイオードとボタン電池」など、構造や仕組みについて観察し、考察させる問題を毎年出題していますが、今年は袋の中身が「星座早見」でした。お土産として持ち帰った受験生にとっては、これまでの入試の中で一番使い道のあるものだったかもしれません。
問１～問３は、実際に星座早見を使えば簡単にわかる問題。問４～問５は、星座早見を使わずに答えることが要求される学校も多い、言わば難関校の典型問題です。

問１

実際に与えられた星座早見で指示された日時に合わせ、一等星（☆印）の数を数えるだけですから、絶対に間違えたくない問題です。時間配分さえ間違えなければ、難なくクリアできるはずです。

問２

これも、北斗七星やカシオペヤ座の向きに注意しながら探すだけの問題です。
もし、間違えるポイントがあるとすれば、北の地平線を見た状態なので、星座早見を逆さまにして使わなければならないといいうことだけでしょう。
星座早見を使う時に、観察する方角が下になるように持つというのは基本中の基本ですから、武蔵中学合格をねらう受験生であれば間違えてほしくない問題です。

問３

決して難しくはありませんが、きちんと筋道立てて説明するためには、論理的な思考が必要とされる問題です。
観察開始時点ですでに西の空に沈みかけている「うしかい座」、全体が地平線上に出るのが23時くらいになってしまう「ぎょしゃ座」、観察する時間中ずっと地平線の下にある「しし座」、観察する時間中ずっと観察できる「はくちょう座」の４つですから、撮影順は明らかに「うしかい座→はくちょう座→ぎょしゃ座」で、撮影できないのが「しし座」です。
あとは、いかに論理的に理由の記述ができるかが鍵でしょう。

問４

これは、星座早見がなくても正解してほしい基本問題です。
仮に分からなくても、適当な日付で23時に合わせ、その１ヶ月後の日付と合わさっている時刻を読み取れば分かるのですから、確実に得点したい問題です。

問５

易しくはありませんが、難関校を受験するお子様であればできてほしい問題です。ただし、計算式も含めてかなり論理的な記述を求められる問題ですから、この問題を解き切れるだけの試験時間が残っているかどうかが問題でしょう。
経度で5度分の違いですから、日周運動であれば約20分間分、年周運動であれば約5日間分早める必要があります。当然、求められている２つの方法は、１つが時間をずらす方法、もう１つが日付をずらす方法になるでしょう。

合否を分けた一題

例年の武蔵中学校の入試であれば、特徴的な「袋の問題」への対応方法を、「合否を分けた一題」として解説したいところです。しかし、今年の問題は、いつものように観察力・分析力を求められるものではなく、入念な準備をしてきた受験生にとってはちょっと予想外の出題内容でした。やや一般的な問題であったために、準備をしてきた人とそうでない人との差があまりつかなかったものと思われます。
そうなると、むしろ大問１の問３をミスなくクリアし、それを踏まえた問４に正解できるかどうかが合否を分けた可能性が高いと言えるでしょう。

【問題】大問[１]　問４（一部、問３の解説を含む）

図３で与えられたＡ・Ｂ・Ｃの位置が、それぞれ作用点・支点・力点を意味していることに気付いたでしょうか。
図１・図２からの誘導もあり、何気なく図３を見ると、クレーンの腕の付け根部分をＢとしているかのように感じてしまいます。しかし、実際にクレーンが物体をつり上げているときに、もしつ力のつり合いがくずれて倒れることがあるとしたら、どこを支点（回転の中心）として傾くでしょうか。明らかに、クレーン側の車輪の位置が支点となることが分かるはずです。

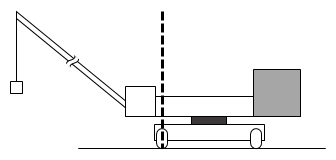
つまり、図３のＢを示す点線は、クレーンの腕の付け根部分ではなく、車輪の位置にひいてあったのです。
したがって、問３で求められている「Ｂにあたる線」の作図は、右のようにかくのが正解です。
そして、つり合いを計算する問４も、当然この位置（左側の車輪または支え）を支点として計算していきます。

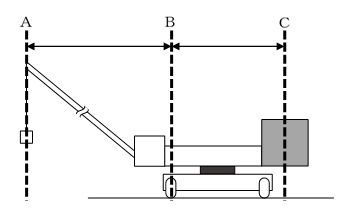
まず、支えを出していない状態では、右の図のようにＡ・Ｂ・Ｃの位置を考えることができます。
図４で与えられた条件から、BC間の距離は
（2.4÷2）＋2.1 ＝ 3.3（m）　

また、「つり上げてよい物の重さは11tまで」ということは、その2倍にあたる22tが、30tのおもりとつり合うことになりますから、つり合う重さの逆比より、
AB：BC ＝ 30：22 ＝ 15：11

ここで、BC ＝ 3.3（m）ですから、AB ＝ 4.5（m）です。

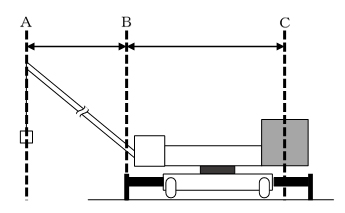
次に、問題の図５のように、左右に1.5mの支えを出した場合を考えます。そうすると、右の図のように、Ｂの位置が左に1.5mずれることになりますから、AB間は1.5m小さくなり、BC間は1.5m大きくなります。
したがって、ABとBCの距離の比は、
　（4.5－1.5）：（3.5＋1.5）＝ 3：5
つり合う重さの比はこの逆比ですから、Ｃの位置に重心がある30tのおもりとちょうどつり合う物の重さは、
　□：30 ＝ 5：3　　→　　□ ＝ 50（t）

ただし、つり上げてよい物の重さはこの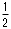までですから、50× 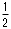＝ 25（t）
半分にしているだけですから計算は難しくありませんが、少し気を抜くと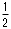を忘れてしまいます。入試では、そのわずかな気のゆるみが合否を分けますので注意してください。