算数の合否を分けた一題
駒東中入試対策・算数の合否を分けた一題(2017年度)
難易度分類
| 1 | (1) A (2) A (3) B (4) B |
|---|---|
| 2 | (1) ① A ② A (2) 作図 A ① A ② A |
| 3 | (1) ① A ② A (2) B (3) B |
| 4 | (1) 作図 A 面積 A (2) ① B ② B (3) C |
A…駒場東邦中学合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題
出題総評
最後の立体切断以外は、極端に難しい問題はありませんでした。ある程度の基礎力を持っている受験生であれば、すんなり誘導に乗ることもできたはずですし、十分な手応えが感じられたことと思います。
しかし、ただ易しいわけではなく、大問[1]の記述問題や、大問[2]・大問[4]の誘導の美しさなど、随所に出題者のこだわりを感じられる入試問題でした。
問題別寸評
(1)~(3)は、極めて基本的な計算問題と小問集合でした。ここは確実に得点しておきたいところです。一方、特徴的だったのは(4)です。解答欄の大きさから考えても長文を要求しているものではありませんが、実生活の中で算数の考え方が活かされて感動したり、面白いと感じたりした出来事を書かせるという、算数のテストには珍しい記述問題です。2020年の大学入試改革を意識した出題だと考えられますが、お子様によっては度肝を抜かれたかもしれません。
(1)
途中の数字で不安になるかもしれませんが、2017という答えが出たところで自信をもって答えを書ける仕掛けになっていました。昨年に引き続き、2年連続で入試年度が答えの数字になりましたが、来年以降も続くものとは考えない方が良いでしょう。
(2)
和が等しい倍数算ですが、気づくことができたでしょうか。よくある「お金のやり取り」が題材となったものではありませんが、問題の本質がつかめれば易しかったと思います。
(3)
すべて数え上げる問題は、数え漏れや重複に十分注意が必要です。バラバラに数えていくとミスが出ますので、まずは2通りある3個の立方体をはり合わせた形を考え、そのそれぞれについて、もう1個の立方体をどこにはり合わせられるかを考えていくと解きやすいでしょう。
(4)
採点者は個人の経験を知りようがありませんから、内容によって◯×がつくという性質の問題ではありません。あくまで、算数の知識を日常生活に結び付けられるかがポイントでしょう。「感動」「面白い」という言葉につられると、すごい話を書かなければならないかのような錯覚を受けますが、活用例が書ければ問題ありません。
大問[2]は、全体的に易問でした。(1)は、「3:4:5の直角三角形」という知識を持っている多くの受験生にとっては、易しすぎてかえって不安になるような問題だったかもしれませんが、それを知らなくても(2)が解けるようにするための、実に美しい誘導問題です。
(1)
台形ABCDの面積から、直角三角形ABEと直角三角形CDEの面積を引くことで、①の三角形AEDの面積を求めることができます。また、直角三角形ABEと直角三角形CDEが合同であることから、三角形AEDが直角二等辺三角形であることが分かりますので、①で求めた面積から逆算することで辺AEの長さを求めることができます。
この(1)は、直角をはさんだ2辺の長さが3cm,4cmの直角三角形の、斜辺の長さが5cmであることを教えるための誘導問題だったわけですが、多くの受験生は「3:4:5の直角三角形」を知識として覚えているので、かえってためらったかもしれません。
(2)
作図自体は難しくありません。
A1からA2に回転するときの半径が、(1)で求めた知識を使って5cmと分かるので、それを利用して①(線イの長さ)や、②(線イと直線アによって囲まれる部分の面積)を求める問題です。
ミスなく、しっかりと得点しておきたい問題でした。
分数の約分に関する、基本に忠実な出題でした。
問題のテーマ自体は「分数」ですが、問題の本質は、むしろ、「約数」「倍数」といった「整数の性質」だったと言えます。
(1)
435を素因数分解させ、成分が「3」と「5」と「29」の3種類だけであることに気づかせることが、この小問の狙いです。この3つの数字以外では約分できないわけですから、①であれば285が、②であれば377が、それぞれ3,5,29のいずれで割れるかを考えれば良いのです。
簡単ですから、確実に得点しておきたい問題です。
(2)
既約分数(それ以上約分できない分数)が、「3の倍数」「5の倍数」「29の倍数」のいずれでもないことが条件であるという、極めて基本的な問題です。ただし、入試問題で同様の出題がされるときには、要素が2つだけである場合が多いので、解法だけでなく、その理由まで理解できているか否かを試す意図が感じられる問題でした。
3つの要素が重なり合うベン図を考え、そのいずれにもあてはまらない数を求めれば正解です。
(3)
気づけば易しい問題ですが、がむしゃらに探したのでは、時間ばかりかかってしまいます。
いかに効率よく正解を探せたかによって、明確な差が出た問題だと思いますので、この問題を「合否を分けた一題」として、後ほど詳しく解説します。
気づけば易しい問題ですが、がむしゃらに探したのでは、時間ばかりかかってしまいます。
いかに効率よく正解を探せたかによって、明確な差が出た問題だと思いますので、この問題を「合否を分けた一題」として、後ほど詳しく解説します。
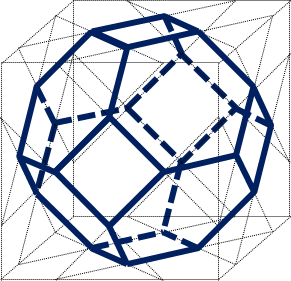
(1)
これは基礎問題ですから、確実に得点したいところです。そして、切断した「立体あ」を想像するためのヒントであるとも言えるでしょう。
(2)
(1)に続き、完成した「立体あ」を想像するためのヒントとなりますが、(1)に比べると難しくなっています。切断後の立体の形が見えていないと、なかなか正確に答えることはできないでしょう。
難易度分析の項目では「B」としましたが、それはこの問題が解答のみを要求する出題形式で、途中式や考え方を書く部分がなかったためです。
レベルとしては、何とか部分点が取れれば良しとすべき問題と言えるでしょう。
(3)
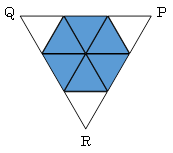
(2)で、「面い」の形が、切断面PQRを右図のように9等分したうちの6個分にあたる正三角形になるということが見抜ければ解けるかもしれません。
ただし、形が分かったとしても、もとの立方体の中から三角すいA-PQRと同じ形を8個分切り取り、重なった部分を戻す作業をしなければなりませんから、正確に解ききるには、ある程度時間もかかります。
この問題は、考え方や途中式などを書く欄が設けれていますので、あるいは考え方だけを書いておいて、実際の計算は後回しにすべきかもしれません。
合否を分けた一題
易しくて合否を分ける問題にはならない大問[2]、難しくて合否を分ける問題にはならない大問[4]に対して、大問[3]は受験生による差がはっきりと表れる問題だったかもしれません。
その中でも、特に(3)は、解法の違いによって、かかる時間も正確さも左右される問題だったように思います。
この問題を、短時間で確実に解けたか否かが、合否を分けた可能性が高いと思います。
【問題】大問[3](3)
まずは、435を素因数分解します。(実際には、(1)の段階で素因数分解はしていると思います。)
435 = 3 × 5 × 29
つまり、既約分数ではない数になるためには、3,5,29いずれかの倍数になっていれば良いことになります。
そこで、まずは比較的小さい周期で考えることのできる、3と5の倍数の現れ方を見てみます。
当然、最小公倍数は15ですから、15周期で考えることになります。

こうして見てみると、「4」の位置か「11」の位置に29の倍数が入ることが、約分できる数(3・5・29の倍数)が最も長く連続する条件であると分かります。
では、29の倍数の現れ方には、どのような規則があるのでしょうか。
上記の1~15の周期の中で、29の倍数がどの位置に現れるかを考えてみましょう。
それぞれ、15で割ったときのあまりによってどの位置にくるか分類できます。
29は、15の倍数である30より1だけ小さい数ですから、29ずつ大きくなる29の倍数は、下の図のように1つずつ左の列に現れることになります。

したがって、以下の2ヶ所で4個連続するのが、最も長く続く並びとなります。

あとは、問題の指示に従って、正確に答えを書いてください。
(答え)
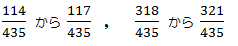
駒東中入試対策・関連記事一覧
駒東中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 時期ごとの算数の学習法の提案(5年生)
- 時期ごとの算数の学習法の提案(6年生)夏休みまで
- 時期ごとの算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から駒場東邦中学入学を目指す皆さんへアドバイス
- 算数の合否を分けた一題(2009年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
駒東中入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2009年度)
- 算数の合否を分けた一題(2009年度)
- 国語の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)