算数の合否を分けた一題
駒東中入試対策・算数の合否を分けた一題(2009年度)
平成21年
合格者平均が120点満点で90点を超えるという高得点勝負で、ミスが許されないという点では厳しい受験になりました。
1・3は駒場東邦の合格を目指す受験生ならば、全問正解しておきたい内容です。
2は知識の有無で所要時間や正解率が大きく変わってくる、まさに「合否を分けた一題」と言えるでしょう。
4は(1)の時点で頭の中で組み立てるのが厳しく、点数に結び付けるのは難しいかもしれません。もし(2)までできたとしても、(3)は試験時間を考えると、不要ともいえる内容です。
出題別難易度
1 AAAA
2 ABB
3 AAA
4 BBC
A…駒場東邦中合格を目指すなら確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えればよしとする問題
合否を分けた1題
2
右下の図のような、正三角形4つで囲まれた立体があります。点Pははじめ頂点Aにあり、1秒ごとに他の3つの頂点のうちの1つに移動します。例えば、2秒後に点Pが頂点Aにあるような動き方は、
A→B→A A→C→A A→D→A
の3通りあります。
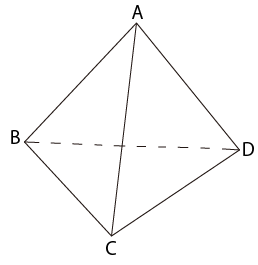
(1) 3秒後に点Pが頂点Aにあるような動き方を、上の例にならってすべて答えなさい。
また、3秒後に点Pが頂点B、C、Dにあるような動き方は、それぞれ何通りありますか。
(2) 4秒後に点Pが頂点Aにあるような動き方は何通りありますか。
(3) 5秒後に点Pが頂点Aにあるような動き方は何通りありますか。
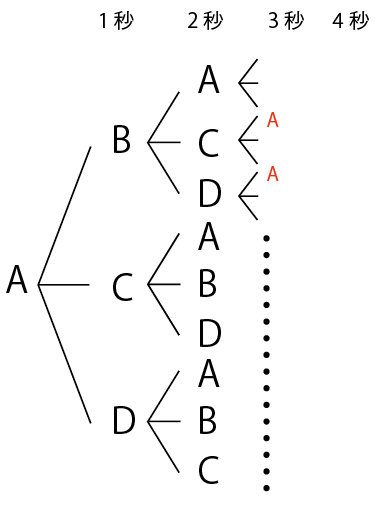
このように樹形図を書いて調べ上げることも可能です。この場合は手際良く正確に書き出す、緻密な作業遂行力が問われます。
ただ、いかがでしょうか。駒場東邦中の先生方は、この地道な作業が出来る生徒を求めているのでしょうか?
ここで一つ、基本的な問題を考えてみましょう。
PからQまで、最短距離で行く方法は何通りあるかという出題です。
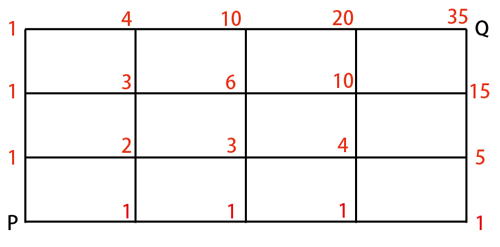
これなら誰しも、嬉々として数字を書き込んでいって35通りと、正答を導くことができるでしょう。
しかし何故、下と左の数字を足してよいのでしょうか?場合の数は、むしろ掛け算で計算していくことのほうが多かったはずですよね?
ここで鍵になるのが「直前にどこにいるのか?」ということです。最後にQに到着するためには、その直前には必ずQの左か下にいる必要があります。したがってQの左か下に到達していれば、あとはそれぞれQに来る1通りずつしかないわけです。したがって下の樹形図のようなイメージで、単純に足せばよいということが分かります。
さあ、実はこの発想がこの2にも適用できるのです。
この三角錐を真上から潰してみましょう。
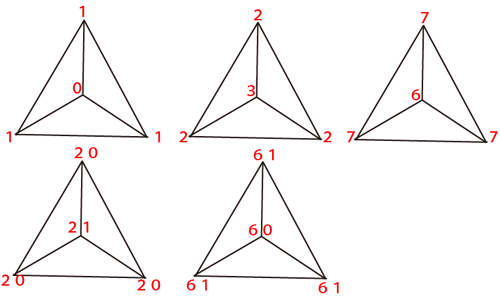
この解法を知っていれば、5分もかからずに正解を導くことも出来たのです。
2をたやすく完答することができるうえ、残りの問題に割くことが出来る時間も増え、結果として高得点に結びついた生徒も多かったことでしょう。
合格した生徒の感想を聞いても「多少ミスはしたものの、1 2 3で確実に得点できた」という声が大多数を占めました。難問であった4を話題に挙げる生徒が少なかったことからも、基本的な問題を、いかに取りこぼしをせずに切り抜けたのかが合否の分水嶺になったようです。
平成21年は、まさに知識の有無が合否を分けたといっても過言ではありません。
駒東中入試対策・関連記事一覧
駒東中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 時期ごとの算数の学習法の提案(5年生)
- 時期ごとの算数の学習法の提案(6年生)夏休みまで
- 時期ごとの算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から駒場東邦中学入学を目指す皆さんへアドバイス
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
駒東中入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2009年度)
- 国語の合否を分けた一題(2012年度)
- 社会の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)

 (13 投票, 平均値/最大値: 4.92 / 5)
(13 投票, 平均値/最大値: 4.92 / 5)