算数の合否を分けた一題
攻玉社中学入試対策・算数の合否を分けた一題（2020年度）
難易度分類
| ［1］ | (1)A (2)A (3)A |
|---|---|
| ［2］ | (1)A (2)A (3)A (4)A (5)B (6)A (7)A |
| ［3］ | (1)A (2)A (3)A (4)B (5)B |
| ［4］ | (1)A (2)A (3)A (4)A (5)B |
A：攻玉社合格を目指すなら必ず得点したい問題
B：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
出題総評
例年、大問1で計算小問と約束記号や数の性質、大問2で規則性、大問3で速さのグラフ、大問4で平面図形、大問5で立体図形と単元が決まっている本校の入試でしたが、今年は出題される問題の傾向が大きく変わりました。大問1は計算問題を含む小問が3つ、大問2は文章題の小問が7つ、大問3,4は各単元にわかれての形式でした。
詳細については大問1が計算2問＋小問1問（約束記号）、大問2は割合の文章題が2問・速さが1問・規則性が1問・単位計算の文章題が1問・和と差の文章題が1問・平面図形が1問・大問3は割合の文章題・大問4は平面図形と点の移動の問題でした。
問題別寸評
どの問題も本校に合格するためには落とすことは出来ません。時間の目安としては5分ほどです。
(1)
(2)
分数の混合計算問題です。こちらも本校合格のためには落とせません。
(3)
これまでの入試でも何度も目にしてきた約束記号の問題です。ルールに従って順番に計算をするだけなのでこちらも落とせません。
いずれも各単元の標準的なレベルの小問群で、(5)以外は全問正解したいところです。
(1)
速さから通過算の問題です。トンネルと橋の長さの違い・かかった時間の差から列車の秒速が出せます。ここから列車の長さがわかります。
(2)
容積の単位換算の問題です。1㎥=1000L、1L=1000mLであることを利用すると答えが求まります。
(3)
割合から損益算の問題です。定価の20%引き・35%引きの売り方の違いが、432+216=648円にあたると考えます。定価がまず求まりますが、問われているのが仕入れ値なので気をつけましょう。
(4)
規則性から日暦算の問題です。7月3日から見て、10月28日が何日後であるのか、1か月ごとに調べて丁寧に求めるようにしましょう。
(5)
和と差の文章題から、少し捻られた鶴亀算の問題です。情況は以下のようになります。
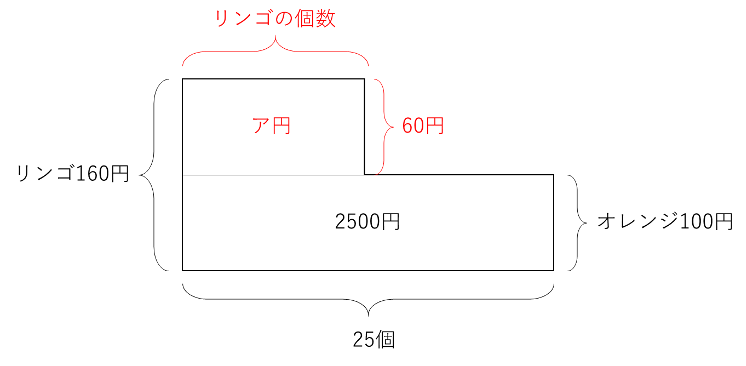
合計金額が3000円=100の倍数で、出たおつりで1個100円のオレンジを買った（その合計金額も100の倍数）ことから、上図の面積図全体の金額も100の倍数です。図のアが60の倍数でもあることから、60と100の最小公倍数である300円とするとリンゴの個数は300÷60=5個となります（次の300の倍数である600とすると、2500+600=3100円となり3000円をオーバーしてしまうので不適切です）。以上の事から、追加したオレンジの個数もふまえると答えが求まります。
(6)
割合から仕事算の問題です。製品を作る仕事量全体を30と36と45の最小公倍数である180とおき、機械が1時間あたりに働く仕事量を求めると、A1台とB1台の合計では180÷30=6、B1台とC1台の合計では180÷36=5、A1台とC1台の合計では180÷45=4と求まります。それら3つの値の和がA2台・B2台・C2台が1時間にする仕事量の合計となるので、2で割るとA1台・B1台・C1台が1時間にする仕事量の合計がわかります。
(7)
直角三角形を、1点を中心として回転移動させる平面図形の問題です。求めるべき面積は、半径10㎝で中心角が90°のおうぎ形から、半径8㎝で中心角が90°のおうぎ形を引いたものになります。回転移動の典型題なので、他の問いも含めて落とせないところです。
ここからは大問になります。濃度の異なる食塩水同士を混合する割合の問題です。今年は本問を、合否を分けた一題として詳細を後述します。
面積比と点の移動の考え方が融合した平面図形の問題です。
(1)
問題の条件から、立体の底面である台形の面積は18000÷10=1800㎠です。その上底が30㎝、高さが40㎝とわかっているので下底であるCDが求まります。
(2)
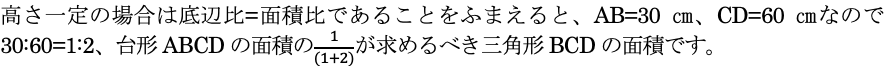
(3)
ここからは点の移動の考え方です。
まず、20秒後にPは1×20=20㎝進み、Qは2×20=40㎝進みます。PはAからBに20㎝進んだところに、QはちょうどHにいます。問題文の条件でPR+QRが最小になるときは、PからQまでを直線で結んだ場合です。そうすると、三角形PRA・三角形PQEのピラミッド型相似の考え方からARの長さが求まります。
(4)
立体の高さが10㎝で、PQの長さが10㎝になるとPもQも止まるということから、それはPのちょうど真下にQがいるときであるとわかります。PとQが進む距離の合計が、ちょうど底面の台形1周分と考えれば答えが求まります。
(5)
2点が止まる60秒後、Pは1×60=60㎝進むのでBからCに30㎝進んだところに、またQはその真下（FからGに30㎝進んだところ）にいます。求めるべき立体は、三角形PCDを底面とした三角柱になります。(2)で三角形BCDの面積が1200㎠とわかったので、ここでも高さ一定→底辺比=面積比を用いるとBC:CP=50㎝:20㎝=5:2となり、三角形PCDの面積がわかるので答えが求まります。最終問ですが、決して難解な問題などではなく、時間の許す限りは正解したいところです。
合否を分けた一題
今回は、大問3について合否を分けた一題として紹介しましょう。濃度の違う食塩水同士を2種類あるいは3種類混ぜ合わせる本問は複数の解法が存在し、各々の問題でどの解法を選択すべきかという点を考えると重要な問題であると言えます。
(1)
濃度3%の食塩水A400ｇと、濃度8%の食塩水B600ｇを混ぜ合わせるので、各々の食塩の量を考えると(400×0.03+600×0.08)÷(400+600)=0.06→6%となります（勿論、濃度の異なる食塩水同士の混ぜ合わせの問題なので、面積図や天秤を使って答えを求めてもかまいません）。
答え：6%
(2)
濃度3%の食塩水Aと、濃度12%の食塩水Cを混ぜ合わせたら濃度が9.5%となったので、平均算と捉えて天秤を書きます。
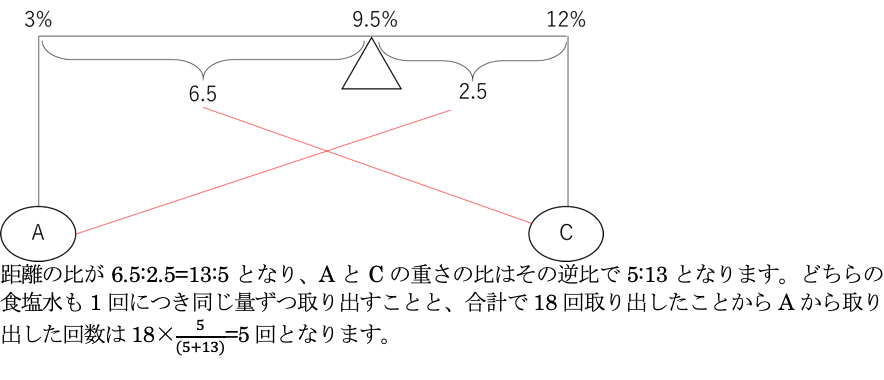
答え：5回
(3)
混ぜ合わせる組み合わせはAとB、BとC、AとCの3通りがありますが、このうち濃度が3%のAと濃度が8%のBはどんなに混ぜ合わせても10.6%になることはありません。
次に、濃度が3%のAと濃度が12%のCを混ぜ合わせると以下のようになります。
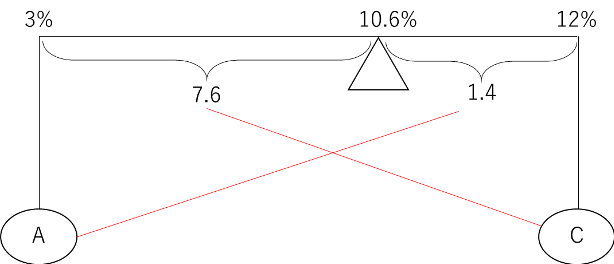
7.6:1.4=38:7となり、必要なAとCの食塩水の重さの比は逆比で7:38となります。ここから、取り出す回数の合計は7+38=45回となります。
続けて、濃度が8%のBと濃度が12%のCを混ぜ合わせると以下のようになります。
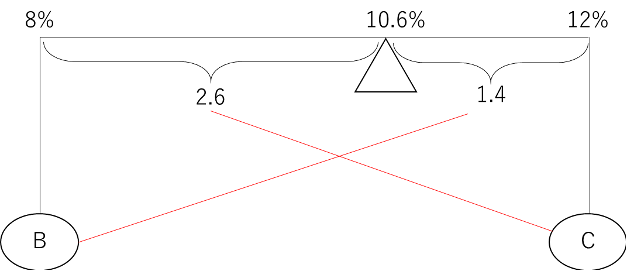
2.6:1.4=13:7となり、必要なBとCの食塩水の重さの比は逆比で7:13となります。ここから、取り出す回数の合計は7+13=20回となり、この場合が取り出す回数の合計が最も少ない場合であるのでBが7回、Cが13回となります。
答え：B…7回、C…13回
(4)
混ぜ合わせる食塩水の比も2:3:5となるので、濃度3%の食塩水Aを200ｇ・濃度8%の食塩水Bを300ｇ、濃度12%の食塩水Cを500ｇ混ぜた、と仮定して水そうPの食塩水に含まれる食塩の量と全体の量を求めます。
食塩の量…200×0.03+300×0.08+500×0.12=90ｇ
全体の量…200+300+500=1000ｇ
よって、90÷1000×100=9%となります。
答え：9%
(5)
先ほどの(4)と同じようにして、問題文の条件から各々の食塩水の重さをA、B、C、Dの順に200g、500g、700g、600gとします。
濃度が判明しているA、B、Cの食塩水について含まれる食塩の量の合計と全体の量の合計を求めます。
食塩の量…200×0.03+500×0.08+700×0.12=130ｇ
全体の量…200+500+700=1400ｇ
Dも混ぜてできた、水そうPの食塩水については
全体の量…1400+600=2000ｇ
食塩の量…2000×0.1085=217ｇ
となるので、Dに含まれる食塩の量は217-130=87ｇ、全体の量は2000-1400=600ｇとなります。
よって、Dの濃度は87÷600×100=14.5%となります。
答え：14.5%
(1 votes, average: 2.00 out of 5)
Loading ...
攻玉社中学入試対策・関連記事一覧
攻玉社中学入試対策・同じ教科（算数）の記事
攻玉社中学入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（算数）の記事
