算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

攻玉社中学入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	(1)A　(2)A　(3)A　(4)A　(5)A
［２］	(1)A　(2)A　(3)A　(4)A
［３］	(1)A　(2)A　(3)A　(4)B　(5)B
［４］	(1)A　(2)A　(3)A　(4)B　(5)B　(6)B
［１］	(1)A　(2)A　(3)A　(4)A　(5)A
［２］	(1)A　(2)A　(3)A　(4)A
［３］	(1)A　(2)A　(3)A　(4)B　(5)B
［４］	(1)A　(2)A　(3)A　(4)B　(5)B　(6)B

Ａ：攻玉社合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断してとばすべき問題

出題総評

昨年と同様、今年は大問が４つという構成でした。各設問の内容については例年通り、大問１が計算問題及び小問集合、大問２は規則性、大問３は速さに関する問題、大問４は平面図形及び立体図形でした。出題傾向は2013年から変わりませんが、昨年と今年は平面図形と立体図形が大問４の中で合わせて出題されている形式が続きました。各問において、前半の問題が後半の問題を解く上での誘導になっていることも本校の入試における特徴といえます。難易度はいずれもオーソドックスな問題からの出題であったため例年より解きやすかったのではないでしょうか。

問題別寸評

【１】計算と小問集合

（1）1.25の形を利用する工夫する計算。
　　計算結果は　1.25×210＝262.5　　　262.5

（2）四則計算の逆算。　　　　　　　　　1.5

（3）分数の四則計算。　　　　　　　　　3/8

（4）３つの数をある整数で割ると余りが等しくなる問題。
差の約数に注目しましょう。　　　　10

（5）5枚移したあとの差は10枚であることに気づけば
　　容易に解けたでしょう。10÷2×（17＋15）＝160　　160枚

【２】規則性の問題。

①３つの数の合計が１つ前の円の３つの数の合計の２倍になっている。
②円の中３つの数字は連続する整数になる。
この２つの規則性に気が付けば容易に解くことができたのではないでしょうか。

（1）３番目の円の３つの数の合計は、6×2×2＝24　
求めるアの数は３つの数の真ん中の数（2番目に大きい数）だから、
24÷3＝8……ア
8番目の円の3つの数の合計は、6×2×2×2×2×2×2×2＝768
768÷3＝256だからイ＝255、ウ＝257
ア＝8　イ＝255　ウ＝257

（2）9番目の円周上の数の和は、
6×2×2×2×2×2×2×2×2＝1536　　　1536

（3）円周上の3つの数の和は、1つ前の円の円周上の3つの数の和の2倍
になります。　　　　　　　　　　　　　1：2

（4）円周上の3つの数の真ん中の数（3つの数の平均）に注目すると
1番目の円，2番目の円，3番目の円，………の順番に
2，4，8，16，32，64，128，256，………というように1の位の数字は
2，4，8，6　の繰り返しになっていることがわかります。
よって1000番目の円周上の数の真ん中の数の1の位は
1000÷4＝250あまり0　より6であることがわかります。
最も大きい数の1の位の数は　6+1＝7　　　　　7

【３】速さ（流水算）

典型的な流水算であるが、円周上を２点が動く際に角速度を利用して解くことを
要求された問題でした。通常、円周上を２点が動く速さの問題を解く場合、
角速度を利用することに気が付かず、計算量が増えたり時間がかかり過ぎたり
することがありますが、今回の出題は（3）で角速度の利用を受験生に促すための
誘導の設問が用意されており、（4）（5）もこれを利用して解答すれば容易に正解することができたのではないでしょうか。

（1）半径15ｍの円周の長さを問われています。
15×2×3.14＝94.2　　　　94.2ｍ

（2） A君の
時計回りの速さは94.2÷60＝1.57ｍ/秒
反時計周りの速さは94.2÷100＝0.942ｍ/秒
（1.57＋0.942）÷2＝1.256
（1.57－0.942）÷2＝0.314
A君の静水時……1.256ｍ/秒
流水の速さ……0.314ｍ/秒

（3）B君は１周するのに80秒かかるので
360÷80＝4.5　　　4.5°/秒

（4）角速度を用いた旅人算（追い越し）です。
A君は時計回りだと60秒で1周するので
360÷60＝6°/秒
360÷（6－4.5）＝240　　　240秒

（5）角速度を用いた旅人算（出会い）です。
A君は反計回りだと100秒で1周するので
360÷100＝3.6°/秒
720÷（3.6＋4.5）＝800/9秒に出会います。
A君は、3.6×800/９＝320°進んだ地点で出会うことに
なりますので、P地点から40°の地点になります。
　　　　　　　　　　　　　　40度

【４】立体図形の切断と平面図形

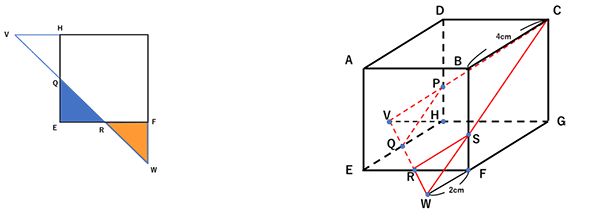
こちらは合否を分けた１題で紹介します。

合否を分けた一題

【４】

立体を切断した時の体積を求めるとともに、立体を切断した時に
できる五角形の切断面をつくる5本の辺を展開図に書き入れ、
平面図形として問うという融合問題でした。
攻玉社を受験する受験生にとっては見慣れている問題であり、
出題としては立体図形、平面図形の両方ともオーソドックスな問題でしたが、
最後の大問4での出題であったため、残りの時間を考えたとき、小問６題をあわてず
正確に解く必要があったこと、前半で間違えるとそのあとの問題の答えがすべて
ずれるということを考えると、まさに合否を分けた１題といえたのではないでしょうか。

（1）（2）

立方体を真上から見ると上図のように
ER：RF＝1：1だから
QE＝FW=2cm
△CBSと△WSFは相似になっているので
BC=4cm FW=2cm　より
BS：SF＝2：1

（3）
BS：SF＝2：1　よりSF=4/3cm
三角すいS-FRWの体積は、2×2÷2×4/3＝8/3　㎤
三角すいP-HQVの体積も同様に　8/3　㎤
三角すいC-GWVの体積は、6×6÷2×4×1/3＝24㎤
求める体積は、三角すいC-GWVからS-FRWとP-HQVを
引いて求めることができる。
24－8/3×2＝200/9　　　　　　　　　200/9 ㎤

（4）
△SFWと△SFRは合同なのでSW=SR
△CBSと△WSFは相似だからCS：SW=2：1
よってCS：SR＝2：1
（5）

展開図に直線を書き入れると右図のようになります。
それを拡大した図が下の図になります。

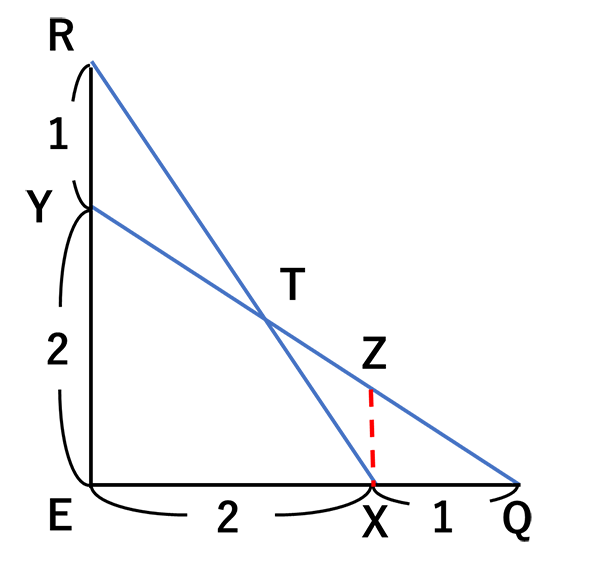
RY：YE=1：2　　EX：XQ=2：1になっている。
YEの長さを2とするとZXの長さは
２×1/3＝2/3となります。
△RYTと△QXTは相似なので
RY：ZX＝1：2/3＝3：2だから
RT：TX＝3：2

（6）

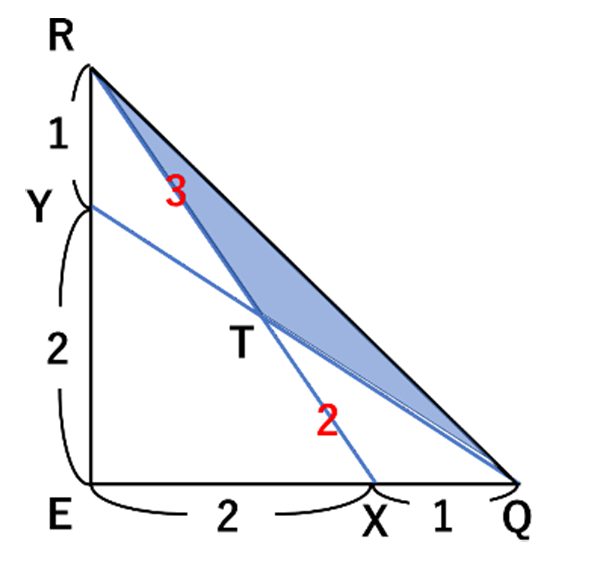
△TRQの面積が△RETの何倍になっているかを
考えます。
EX：XQ=2：1だから
△RXQは全体の1/3倍となります。
さらに、△TRQの面積は△RXQの面積の3/5倍だから
△TRQの面積は全体の
1/3×3/5＝1/5
△RET=２㎠だから
△TRQの面積は、２㎠×1/5＝0.4㎠　　　　0.4㎠　