算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

攻玉社中学入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1)A　(2)A　(3)A　(4)A　(5)A
［２］	(1)A　(2)A　(3)B　(4)B　(5)B
［３］	(1)A　(2)A　(3)ア…A　イ…A　(4)カ…B　キ…C
［４］	(1)A　(2)A　(3)①…A　②…A　③…C

Ａ：攻玉社合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断してとばすべき問題

出題総評

昨年が大問５つであったのに対し、今年は大問が４つという構成でした。各設問の内容については例年通り、大問１が計算問題及び小問集合、大問２は規則性、大問３は速さとダイヤグラム、大問４は平面図形及び立体図形でした。（なお、昨年は大問４が平面図形、大問５が立体図形の出題なので今年は大問４にその２分野が凝縮された形となります）各問において、前半の問題が後半の問題を解く上での誘導になっていることも本校の入試における特徴と言えます。

問題別寸評

［１］

(1)

答　
小数の基本的な四則演算。忠実に計算するだけですが、７．８×０．８ではなく、先に７．８÷１．３＝６と計算するほうが少し楽でした。

(2)

答　
分数の逆算問題。焦らず、しっかりと一つ一つ求まるところは丁寧に逆算していきましょう。(1)とあわせ、ここでの失点は避けたいところです。

(3)

答　ア…３　イ…
簡便法の問題。本校でおなじみの導入部分が問題アにあるので、難しくはありません。分母の２数において、各々でどれだけの差があるかに注意が必要です。イの計算において、初めと終わりの分数だけが残ることも知識として頭に入れておきましょう。

(4)

答　１．１５倍
割合の一行題。問題文の情況を式にして捉えると分かり易いでしょう。太郎×０．２３＝次郎×となり、太郎を①とおいて次郎を求めるだけです。

(5)

答　午後１時分
時計算の問題。６回目までの時刻をすべて求める必要はありません。このあとから数えて、１回目は７時台、２回目は８時台、３回目は９時台、４回目は１０時台、５回目はちょうど１２時、６回目は１３時台です。あとは、ぴったり１時の状態から計算すれば答えが求まります。

［２］

等差数列をテーマにした、規則性と数表の問題。詳細は、合否を分けた一題として後述いたします。

(1)

答　１９７

(2)

答　７２

(3)

答　７７０

(4)

答　３１番目

(5)

答　３６番目と３７番目

［３］

学校から公園までを往復する３人の動きを考えていく、速さとダイヤグラムの問題。いかに、ダイヤグラムの中にある相似形を利用できるかがカギとなります。

(1)

答　４：１
A君とB君の行きのグラフに着目してみましょう。

砂時計相似が見つかります。ここから、問題で問われている比が求まります。

(2)

答　１１２０ｍ

(1)

君の行きのグラフに着目してみましょう。>の答えから、学校から郵便局までの道のりも求まります。

(3)

答　ア…分速１４０ｍ　イ…分速１６０ｍ
アについては、A君が学校から郵便局までの１１２０ｍを８分で進んでいるので求まります。また、イについてもB君が同じ距離を８－１＝７分で進んでいるので求まります。

(4)

答　カ…１８分４５秒　キ…６分１５秒
カについてはA君の往復の様子から計算できますが、キについては複数の相似を扱うので処理が面倒な問題となっています。

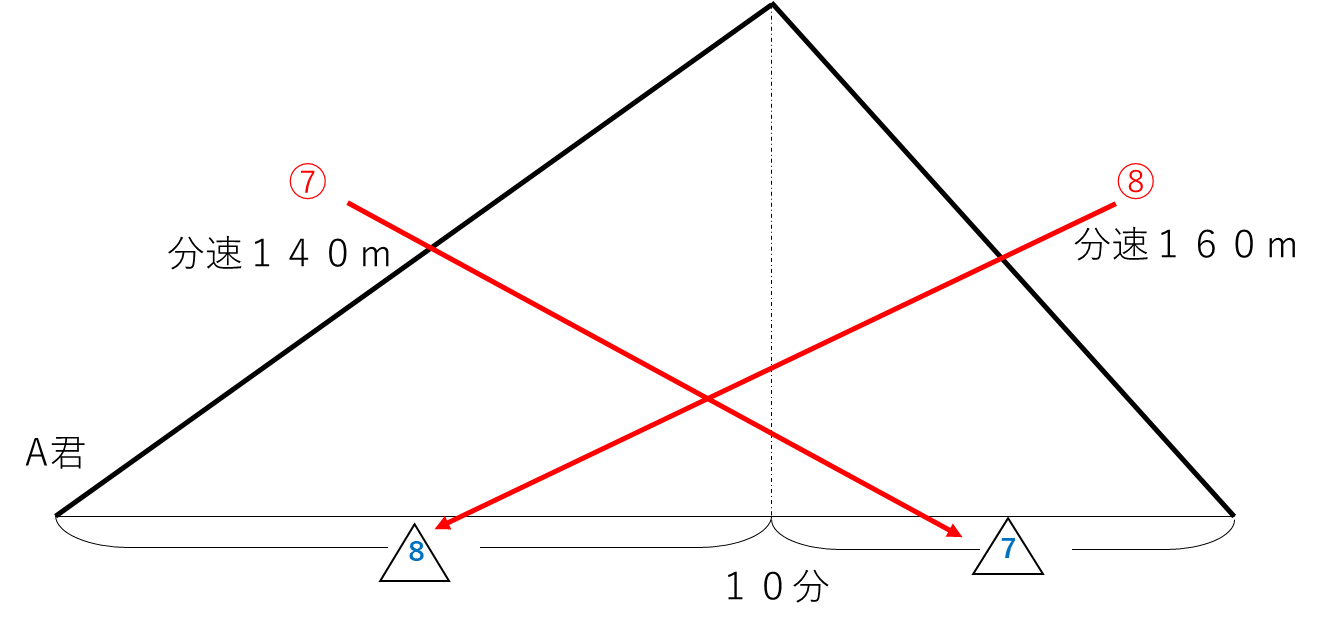
上図のように、同じ距離を進んでいるので時間の比は速さの比の逆比で８：７となります。また、公園についたのは（１１２０＋２８０）÷１４０＝１０分となり、計算していくとカの答えが求まります。
続いて、A君とC君の帰りのグラフについて注目します。

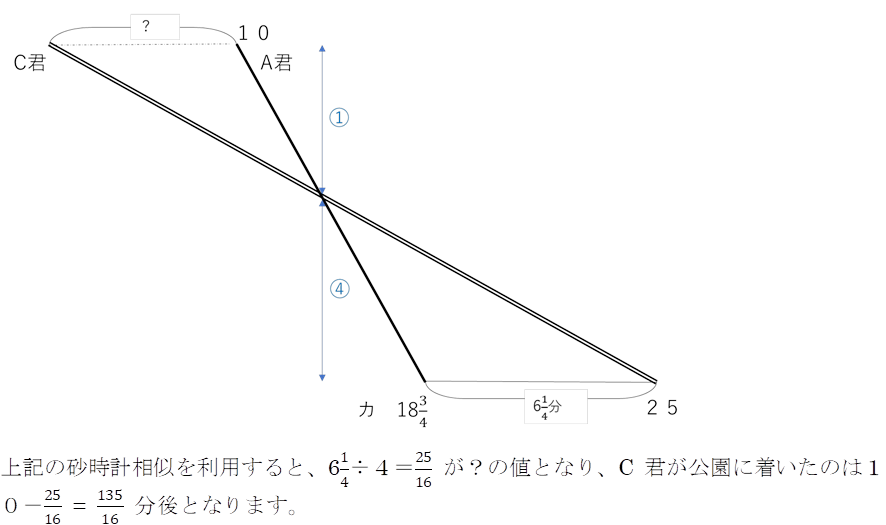
次に、C君の行きのグラフについて見てみましょう。

［４］

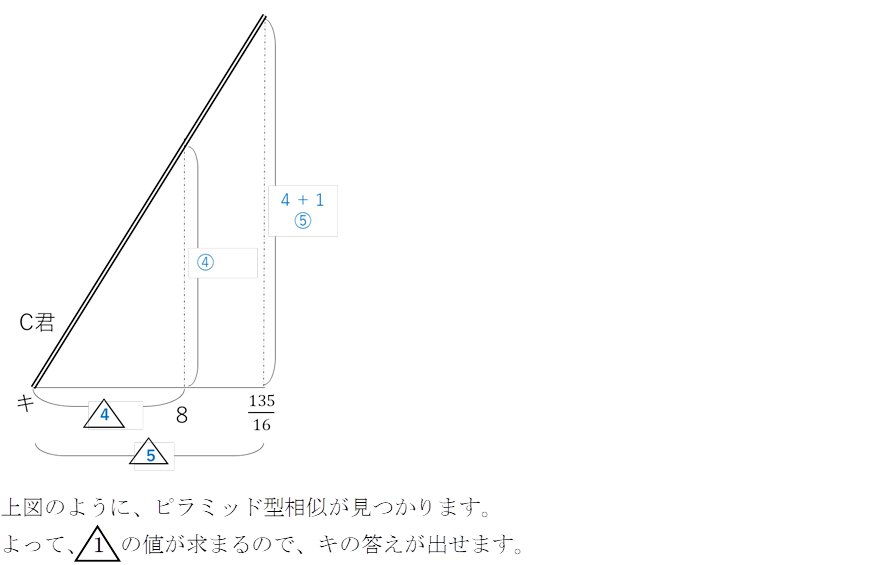
前半の問題群は相似の考え方が絡む平面図形、後半の問題群は相似の考え方を利用・応用させた立体図形の問題。

(1)

答　７．５㎝
まず、辺ABと辺XYが平行であることから△PABと△PXYは相似（ピラミッド）であることが分かります。相似比は、４㎝：１４㎝＝２：７。さらに、辺BCと辺YZが平行であることから△PBCと△PYZも相似（ピラミッド）であることが分かります。ここから、辺PC：辺PZ＝２：７となり、PC＝３㎝ですので答えが求まります。

(2)

答　１：３
XZとYPが交わる点をRとすると、YR：RP＝BQ：QP＝１：３です（△ABCと△XYZが相似、ならびに△ACPと△XZPが相似であるため）。△XYZと△XPZは底辺を両方ともXZとして考えると、面積比は高さの比と同じであることから答えが求まります。

(3)

答　①…４㎠　②…㎤　③…４８㎠
①ABYPが交わる点をRとすると、YR：RP＝BQ：QP＝１：３です（△ABCと△XYZが相似、ならびに△ACPと△XZPが相似であるため）。△XYZと△XPZは底辺を両方ともXZとして考えると、面積比は高さの比と同じであることから答えが求まります。>：XY＝４㎝：１４㎝＝２：７なので、(1)で述べたことからPA：AX＝PB：BY＝PC：CZ＝２：７です。また、△ABCと△XYZは相似であり、各々の面積比が２×２：７×７＝４：４９なので△ABCの面積が求まります。
②三角すいPABCの底面は△ABCで４㎠です。高さを考えます。三角すいPABCの高さ：三角すいPXYZの高さも相似の考え方より２：７です。問題文より、後者は１２㎝なので前者は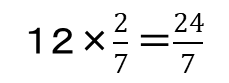㎝となります。ここから三角すいPABCの体積が求まります。
③最後の問題ということもあり、丁寧に作図をしたうえで相似の考え方を発展させなければならない難問でした。他の問題を蔑ろにしてまで、時間をかけて取り組むべき問題ではなかったと言えるでしょう。
三角柱を上から見た図を以下に示します。

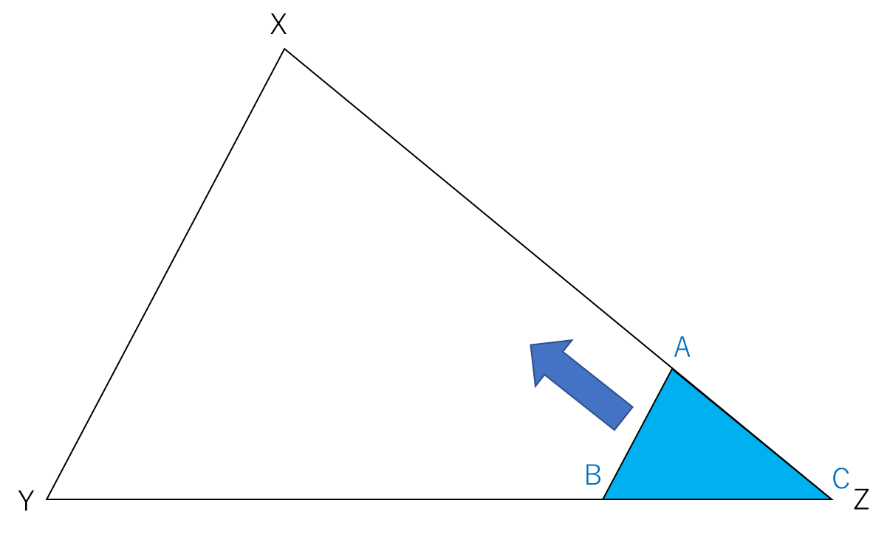
出発時点ではこのようになり、△ABCは点X⇒点Y⇒点Zへと移動していきます。AC：XZが２：７であることをふまえると、その軌跡は下のようになります。

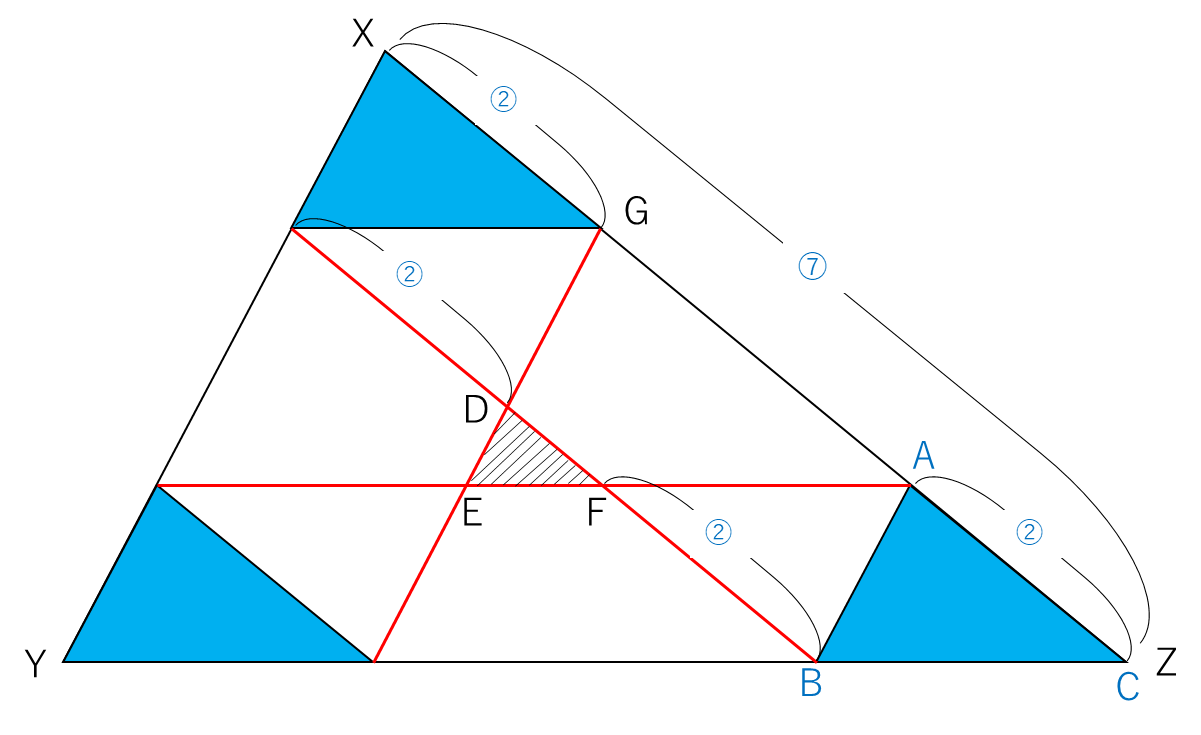
AGは、⑦－②×２＝③でありBDも同じく③です。DFは③－②＝①となり、上図の真ん中の△DEFは△ABCが通れない部分であることが分かります。そして、△XYZと△DEFは相似であり、その比は７：１です。お互いの面積比は７×７：１×１＝４９：１となるので、△XYZから△DEFを引けば答えが求まります。
本問が難しいのは、真ん中に通らない部分（△DEF）があるかが、判定できるか？という点です。このことについては、丁寧に一つ一つの三角形が通った部分を作図しなければ正解に辿り着けなかったでしょう。

合否を分けた一題

今回は、前半の問題群の中で規則性の単元である大問２について合否をわけた一題として紹介しましょう。本校の出題単元として定石となっている規則性ですが、本問の後半になるにつれ、見つけ出した規則をどのように利用すれば良いかが受験生に試される、決して難問ではない良問であったと言えます。

［２］

規則性（数表）

(1)

Aは、１から始まって４ずつ増える等差数列であることが分かります。５０番目の数なので、１＋４×（５０－１）＝１９７です。
答え：１９７

(2)

問題文の条件から、Cを奇数番目と偶数番目にわけて考えます。
奇数番目⇒２，１２，２２，３２，４２…
偶数番目⇒３，９，１５，２１，２７…
上記のように、どちらとも等差数列になっていることが言えます。
１５番目を問われているので、奇数番目について考えていきましょう。

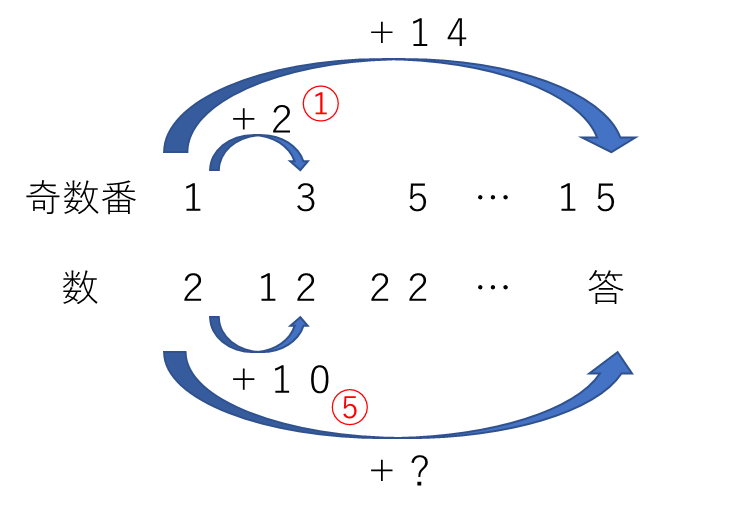
上図より、元の数より１４×５＝７０増えたことになるので、２＋７０＝７２です。
答え：７２

(3)

１番目と２番目、３番目と４番目、５番目と６番目…といった形で２つをセットにして見てみましょう。

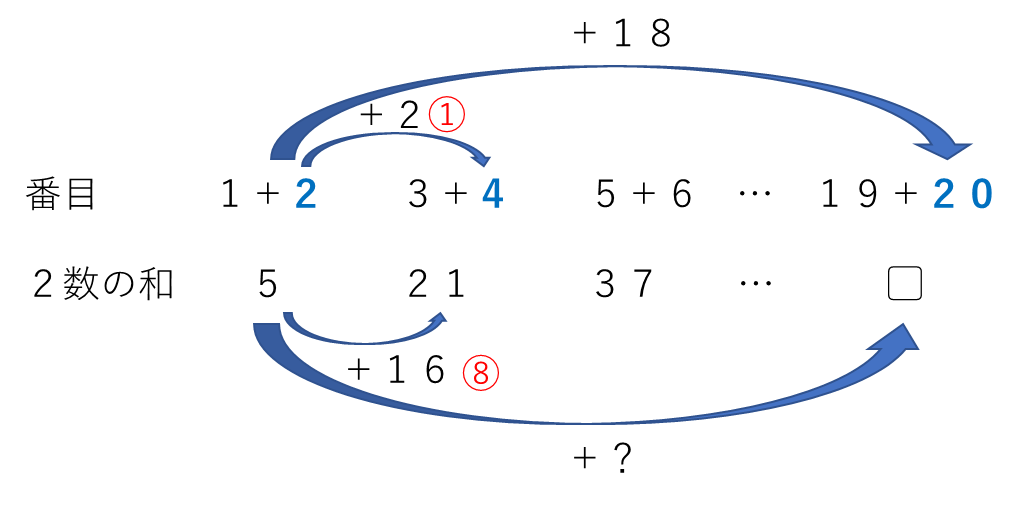
上図より、１９番目と２０番目の和は５＋１８×８＝１４９です。
よって、等差数列の和となるので５＋２１＋３７＋…＋１４９＝（５＋１４９）×１０÷２＝７７０となります。
答え：７７０

(4)

奇数番目と偶数番目で較べてみると、奇数番目は１０ずつ増えるのに対し、偶数番目は６ずつ増えていくので、はじめて１５０をこえるのは奇数番目です。また、１の位が必ず２になっていることを踏まえると、１５２が何番目であるかを求めることになります。

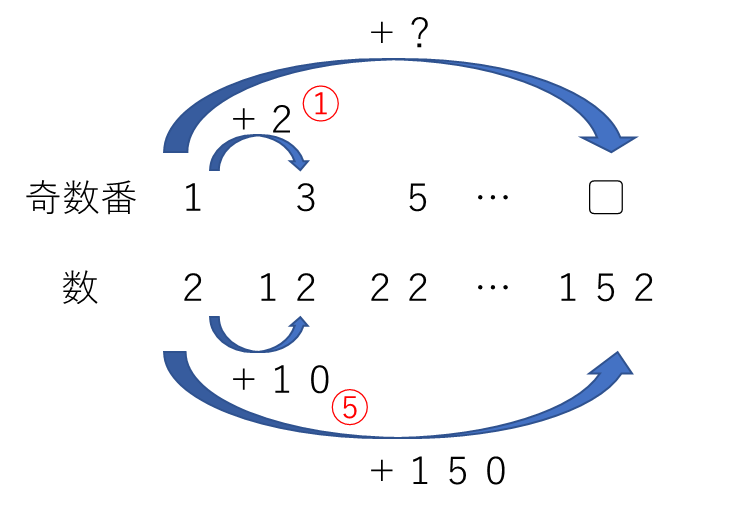
したがって、１＋１５０÷５＝３１番目となります。

答え：３１番目

(5)

まず、奇数番目＋偶数番目の場合を調べます。

ところが、２８２÷１６＝１７…１０となり、この場合ではないことが分かります。
続いて、偶数番目＋奇数番目の場合を調べます。

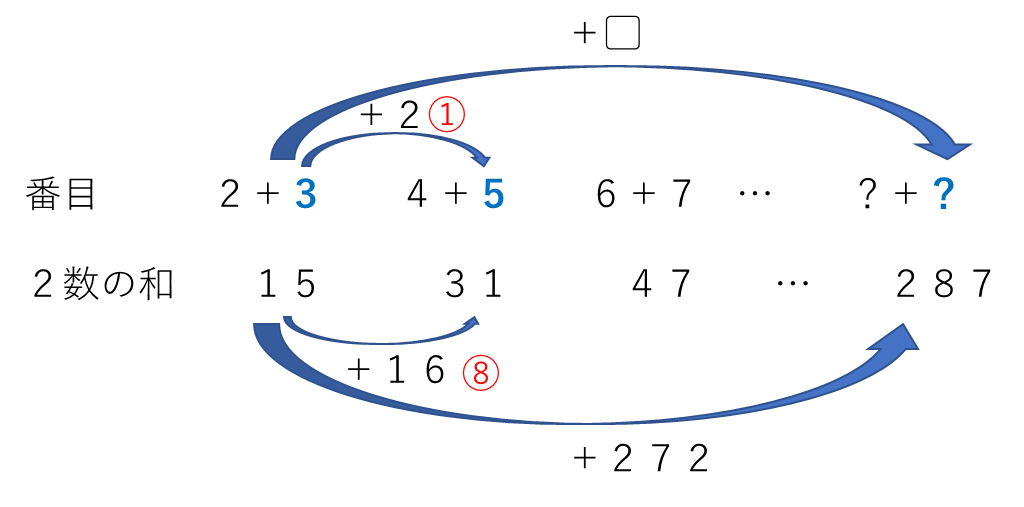
２７２は１６で割り切れるので、この場合です。３＋２７２÷８＝３７番目が後ろとなるので、答えは３６番目と３７番目です。
答え：３６番目と３７番目