算数の合否を分けた一題（2021年度）

算数の合否を分けた一題

開成中入試対策・算数の合否を分けた一題（2021年度）

難易度分類

１	(1) A　　(2) A 　(3) A　　(4)B
２	(1) A　　(2) B　　(3) B
３	(1) A　　(2) A　 (3) B　　(4) C　 (5) C

A…開成合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

問題別寸評

大問１

(1)日暦算

基本的な出題です。2121年は2021年からちょうど100年後ですね。
100÷4＝25回うるう年がありますが、100の倍数である2100年だけはうるう年ではありませんので24回。
平年であれば1年で1曜日進み、うるう年はもう1つ余分に進むと考え、100＋24＝124曜日進みます。
124÷7＝17あまり5　月曜から5曜日進むので土曜となります。

(2)図形と規則

平面を分割する問題のアレンジです。受験生の多くが例題を経験したことがあったはずです。本質を抑えて理解していれば、設問の変化に対応できたはずです。
あらかじめ2本、3本の線が引いてある状態を考え、そこに新たに1本線を引いたときに、いくつの領域が増えるかに着目します。
作図して実験しても確認しつつ、「線を1本引く度に、既に引かれた2＋3＝5本の線に必ずぶつかるため、6つずつ領域が増加する」ことが理解できると、6×100本＝600増加
が求められます。

(3)平面図形

24等分するもよし、辺を延長して正三角形を作るもよし。落とせない一問でした。

(4)数の性質

実際にしばらく割り算のひっ算をしてみると、比較的容易に周期は見えるのですが、小数第96位を求めるとなると、周期を利用する良い解法が見つからず、時間がかかる出題でした。
2の累乗を書き出すしかない問題でしたので、96位はいったん飛ばすか、頑張って書き出すという判断をいかに早く行えたかがポイントです。

大問2

今年は大問3題構成となり、確実に得点すべき問題と、難度の高い問題に二極化しました。その中でも点差をつけるなら大問2の立体図形だったでしょう。
合否を分けた一題として後述します。

大問3

まずは文章を落ち着いて読み取り、ゲームのルールを正確に把握すること。
開成で頻出のルールに基づいて操作する問題は、(1)(2)で作業を通して題意を確認する問題が決まって出題されます。ここで意識したいのは、(1)(2)が高確率でその後の問題への「誘導になっている」ということです。
開成の誘導は、解法の大きな指針を示す案内板のような役割を果たすのですが、今年は誘導に気づくかどうかで、問題の見え方と難易度が大きく変わってしまう、非常に鮮やかな設問でした。
発想の大きな転換が要求されるため、誘導に気づくことができなかった受験生も少なくなかったはずです。
限られた時間の中での最終問。現実的に考えると、(1)(2)(3)をきちんと場合分けして点を固める作戦が良かったのかもしれませんが、開成が求めていた視点を解説しておきます。

さて、どのような誘導になっていたのでしょうか。
(1)(2)(3)における、A君、B君、スコアを並べます。

A君	(1) 0101	(2) 001001	(3) 001001
B君	0000	010001	110110
スコア	0101	011010	111111

何かヒントにならないか考えながらこの解答を眺めてみると…

AとBのカードを、二進法のひっ算で足した結果がスコアになっていることがわかります。
審判がもらうカードが二進法の足し算の繰り上がりを意味し、審判が最初に0を持っているのは、最初は繰り上がりがないからと考えられるわけです。

すると(4)は、スコアのどこかに1がある、つまりAとBの和が100000,10000,1000,100,10,1のいずれかになればよく、Aが1001であることから、AとBの和は1001以上。つまり、100000か10000ということになります。

A君	001001	001001
B君
スコア	100000	010000

これにあてはまるBを考えればよいわけです。
Bが勝つには、最後に審判がもらうカードが0、つまり最後の位で繰り上がらないようにすることにも気をつけましょう。すると、当てはまるBは000111,010111となります。

(5)

B君が勝ちで得点が2になるということは、スコアに1が2カ所含まれる必要があります。
6か所から1を置く2カ所を選ぶと、6×5÷2＝15通り。
しかし、1001より小さい数ではAを引き算できなくなってしまうので、1001より小さい1を2つ含む数である、011,101,110の3パターンを除かなくてはなりません。
15－3＝12通り

合否を分けた一題

2021年度の算数は、難度の低い設問と高い設問に二極化されました。
そのため、合格者平均点が55.8点、受験者平均点が45.8点、合格者と受験者平均の差が10点と、この10年間で最も算数で差がつかない入試になりました。
大問3の難度がかなり高いことを考えると、合否を分けたのは大問2の立体図形。
例年、複雑な切断や立体の重なりを「平面化」する作業を通して分析する力を求めてきた開成ですが、2020年度は(x,y,z)という「座標」の考え方で空間内の移動を捉える数学的要素の強い出題で驚かせてくれました。ひるがえって今年はシンプルな求積問題で、「立体の捉え方」の本質を突くテーマでした。
立体図形の求積の捉え方は大きく2つ、「分割する」か「周りから引く」かです。
どちらの発想も要求される良問で、断頭三角柱の求積方法を学んでいれば、5年生にも是非挑戦してみてほしい一問です。

では、解説です。

(2)

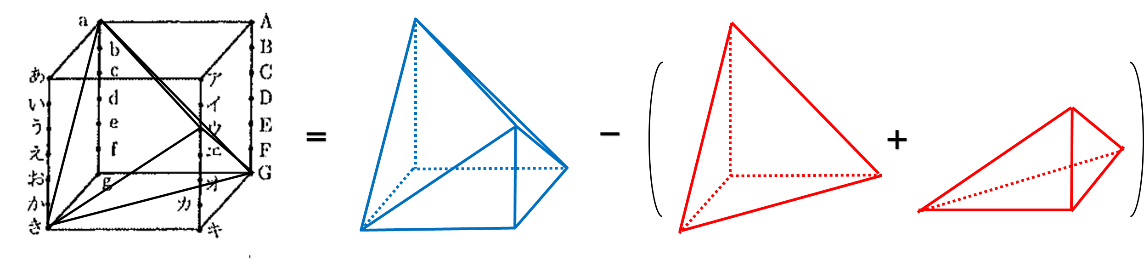
下の図のように、青い7面体から、赤い三角柱を2つ引くと捉えてみましょう。

問題は青い7面体をどのように求積するかです。
こういった複合的な立体を考える手順は2つ。「分割する」か「周りから引く」か。ここは縦に切断して、断頭三角柱2つの和として求めます。左右にパカッと割ります。

底面積は6×6÷2＝18
高さは3つ辺の平均となり、(6＋4＋0)÷3
計算すると1つの断頭柱の体積が60㎤
断頭柱は左右対称で同じ形ですから、60×2＝120㎤

赤い三角すい2つの体積は18×6÷3と18×4÷3となり、合計60㎤。
青い七面体から赤い三角すい2つを除いて、体積は120－60＝60㎤

(3)

(2)が解法の流れを示していますね。同じように、図のような青い7面体から、赤い7面体を引いて求積する方針を立てます。「周りから引く」発想です。

青い7面体を(2)と同じように分割してみましょう。(2)とは向きを変えて、対角線(きG)を結ぶ線で切断します。
赤い7面体も(gキ)に沿って2つに切断します。「分割する」発想ですね。
これで全て、断頭三角柱になりました。

青い断頭三角柱はどちらも底面積が18㎠
高さは3辺の平均となり
(5＋4＋0)÷3と(5＋4＋2)÷3より
体積はそれぞれ66㎤と54㎤

赤い断頭三角柱はどちらも底面積が18㎤
高さは3辺の平均となり
(5＋2＋0)÷3と(2＋4＋0)÷3より
体積はそれぞれ42㎤と36㎤となります。
(66＋54)－(42＋36)＝42㎤

開成は例年、物事を細分化して捉える力を要求する設問が目立ちますが、本問は細かく分けるというよりも、大きくシンプルに捉える力が要求されました。設問に近づいて細部を観察することにくわえ、時に一歩引いて大きくシンプルに捉えてみること。
算数に必要な「細分化=具体化」と「統合=抽象化」の2つの筋力を鍛えたうえで、それらを使いわける技術が要求されました。
来年以降の受験生は、どちらも意識的にトレーニングしていきましょう。

著者：吉岡英慈

この記事は役にたちましたか？