算数の合否を分けた一題（2020年度）

難易度分類

１	B
２	（１）B　（２）B　（３）Ｂ
３	（１）（ア）A（イ）A　（２）①A　②A　③A　④A　⑤A　⑥A　⑦B　⑧B
４	C

A…開成合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

平成30年度　問題別寸評

１

2台の間の距離を考える旅人算と場合の数を組み合わせた問題です。
間の距離を考えさせる問題は、近年様々な学校でも出題され、グラフの見方など練習して
きた受験生も多かったと思います。しかし、開成中はそこに進み方の場合分けという、場合
の数・調べの要素を組み込むことで、一気に難度が上がり解きにくい問題へと変えてきま
した。はじめの条件整理のところで手が止まってしまった受験生も少なくなかったと思われます。

この問題では誘導の小問もありませんので、受験生自身で正解までの段階を考えていかなければいけません。正解までの段階としては、
①グラフから２つのロボットの進み方を考える
②カードの組合せによって、間の距離がどう変化するかを考える
③グラフの状況に一致するよう、カードの組合せを考えていく
というものになります。この順に考えていきます。

①グラフから２つのロボットの進み方を考える
一番のヒントは、1分後～2分後に距離＝０となっていることです。
間の距離のグラフにおいて、間の距離＝０というのは、追いついた時を表します。
グラフで長さの単位が示されていませんので、1目盛り＝①cmとします。つまり、
０～１分後　AがBより②cm前に出た
１～２分後　BがAを追い越し①cm前に出た＝BがAより③cm多く進んだ
２～３分後　Bが①cm差を広げた
３～４分後　BとAの差が変わらない
４～５分後　AがBに追いついて止まった＝AがBより②cm多く進んだ

②カードの組合せによって間の距離がどう変化するかを考える
ロボットの進み方には①～④の４種類あります。２つのロボットがどう進むかによって、差の広がり方（縮まり方）が変わってきます。それを表にまとめておくことで、①で分かったグラフの動きに置き換えることができます。
次のような表にしておくとよいでしょう。

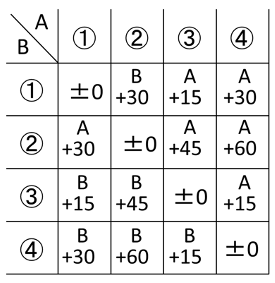
ここから、①の長さ＝15であることが分かり、2回目の動きでAはカード②、Bはカード③であったこともわかります。

③グラフの状況に一致するよう、カードの組合せを考えていく
０～１分後　AがBより30cm前に出た→（A、B）＝（④、①）（①、②）
１～２分後　BがAより45cm多く進んだ→（A、B）＝（②、③）
２～３分後　Bが15cm差を広げた→（A、B）＝（①、③）（③、④）
３～４分後　BとAの差が変わらない→（A、B）＝（①、①）（②、②）（③、③）（④、④
４～５分後　AがBより30cm多く進んだ＝（A。B）＝（④、①）（①、②）

あとは、①が2回、②～④が1回ずつになるよう組合せを探していきましょう。

全ての組合せを考えるのは大変ですが、絞り込みやすいところから考えていくことがポイントであるとおぼえておきましょう。

２

角速度を用いた旅人算の問題です。
大問１に引き続き速さに関する問題でしたが、大問１はどちらかといえば場合の数の要素のほうが強い問題だったのに対し、大問２は純粋に速さに関する出題だったと言えます。
ところが、問題の条件が細かく、また普段の学習ではあまり見たことのないタイプの動きであったため、条件を正しく読み取れたかがポイントでした。（１）が解けたのであれば（２）、（３）も正解できたものと思われます。

（１）①の移動で、点Pが円Xの円周上に来たとき、ちょうど点Bと重ならないといけません。点Pが円Xの円周上に来る場所を点Qとすると、点Bは12分移動して点Qに来ることになります。
同様に点Pが円Yの円周上に来たとき、ちょうど点Cと重ならないといけません。点Pが円Yの円周上に来る場所を点Rとすると、点Cは①～③の移動が行われる32分移動して点Rに来ることになります。
ここから点Bと点Cの移動開始時の位置を答えます。
問題の意味が分かれば難しくありませんが、動き方を勘違いしやすいので丁寧に確認していきましょう。

（２）（１）の図ができたのであれば、点Cが点Bよりも反時計回りに56度進んだ位置にいるとき、点Pが移動を開始すればその32分後に、点Pと点Cが重なることになります。
ここまで分かればあとは、点Bと点Cの角速度の差から求めることができるでしょう。

（３）（１）と（２）をヒントに、⑤の移動で点Pと点Bがちょうど重なる条件を考えます。
点Pが直線上を12分移動して円Yから円Xに戻ってきたとき、点Bと重なるためには、点Bが点Cより時計回りに72度進んだ位置にいればよいことになります。
③の移動が終わった時点で、点Bは点Cより反時計回りに72度進んだ位置にいます。
したがって、（360－72✕2）÷（6－2）＝54分間、④の移動を行えばよいことになります。
以上をまとめると、
直線を10ｍ✕4＝40m
円Xの円周を96度
円Yの円周を108度　　進んだことになります。

このような円周を使った問題や、変則的な時計を用いた問題は、一つひとつの動きを確認しながら解き進めていくと良いでしょう。

３

数字を使った場合の数と規則性に関する問題です。
硬貨を使ってある決まった金額の払い方を考える問題です。（１）は大きな金額ではありませんので、確実に手早く調べ上げたいところです。全体の難度が上がったことを考えますと、この大問は落とすことができません。同じような問題は開成中H23大問3で出題されていますので、イメージしやすかったと思われます。
（２）はある金額を払うのに必要な最低枚数で場合分けをし、それぞれ何通りの金額があるかを考えさせる問題です。前半は問題文の誘導にしたがい調べていきますが、途中で規則を見つけないと後半解きづらくなります。まさに、計算と調べの両方を必要とする開成中らしい出題でした。

（１）（ア）で見つけた場合分けを使います。
「10円玉2枚、5円玉1枚、1円玉3枚」
「10円玉2枚、1円玉8枚」
「10円玉1枚、5円玉3枚、1円玉3枚」
「5円玉5枚、1円玉3枚」
1円玉の枚数を見ると3枚か8枚になります。あとはつるかめ算の解き方を使って、「10円玉2枚、1円玉8枚」で払った人数を求めれば、それが答えとなります。

（２）①は100✕3＋50✕1＋10✕3＋5✕1＋1✕4　と分解できれば問題ないでしょう。
②は、金額の小さい硬貨からたくさん用意すると、1円玉4枚、5円玉1枚、10円玉4枚、
50円玉1枚で合計10枚となりますので、あと100円玉1枚足せばルール3を満たせなくなります。
③と④については実際に書き出してみましょう。そうすると、表の「何通り」の部分が
３、５、７、９、９、７となるので、⑤、⑥に入る数字の予想ができるはずです。その上で実際に調べてみてその予想が正しいことを確認しましょう。
⑦表が1円から49円までの金額で必要な最低枚数を求めたものです。51円＝1円＋50円、52円＝2円＋50円、………、99円＝49円＋50円、であるので、50円から99円までの金額で必要な最低枚数が、1円～49円の表に1枚足したものであることが分かります。
そうすると最も多くても99円の10枚であることが分かります。
以下同様に、50円ずつ増やして考えていくと、
100～149円→0～49円＋1枚→11枚以上必要なものはない
150～199円→0～49円＋2枚→11枚以上必要なものは、1～49円で9枚必要な1通り
200～249円→0～49円＋2枚→11枚以上必要なものは、1～49円で9枚必要な1通り
250～299円→0～49円＋3枚→11枚以上必要なものは、1～49円で8枚以上必要な4通り
と求まります。
⑧ここまで分かればあとは丁寧に作業していきましょう。500円玉が使える金額になるところに注意が必要です。

今回は問題の中で表が作られ、それに従っていけば規則も見つけることができました。問題の中に表がない場合でも、自分で表を作成していくという解き方は身につけておきたいところです。

４

立体図形と光の道筋の問題です。
立方体の小屋の側面と天井に穴が開いており、穴から入った光が床や側面のどこに映るかを考えさせる、空間認識能力が問われる出題でした。類題が灘中H23二日目の大問3でありましたので、解いたことがある受験生は若干有利だったかもしれません。それでも、光の方向や角度に関する情報が少ないためかなりの難問でした。部分点を狙って分かる部分をしっかり答えていくことが得策と思われます。こちらにつきましては、このあとの合否を分けた一題で詳しく解説してまいります。

合否を分けた一題

昨年度より「問題用紙が横開きのもの」になった開成の入試問題ですが、昨年度は最後の大問４で「長い問題文」の問題が出題されました。今年度はそのスペースの広さを活かして、図形の応用問題が出題されました。「長い問題文」と「複雑な図形問題」の両方とも、今後の開成中の算数のポイントとなると思われますので、しっかりした対策が必要でしょう。
また、今年度は全体平均が40点を切り、合格者平均も50点を切る、2016年・2017年並の難度でした。今後も今年度と同程度の難度が続くものと思われますので、取るべき問題を確実に正解していくことはもちろん、少しでも難度の高い問題で正解できるように日頃の学習に取り組む必要があります。
そこで、今年度の合否を分けた一題は、大問４を取り上げたいと思います。

４

この問題を解くためのSTEPは、
STEP1　光の射しこむ方向を求める
STEP２　窓穴１から入った光が、側面に当たる部分を求める
STEP３　窓穴２から入った光が、側面に当たる部分を求める
になります。

そして、このような光や影に関して、立体上の位置を考える問題では、座標軸の考えがとても有効です。座標軸は小学校や塾ではほとんど取り上げませんが、地球上での緯度・経度の
ように「位置を数字で表すもの」として考えると、小学生でも十分使うことができます。
この座標軸を用いて、この問題を解いていきましょう。

まず、立方体Aを基準として下の図のように線を３本引きます。

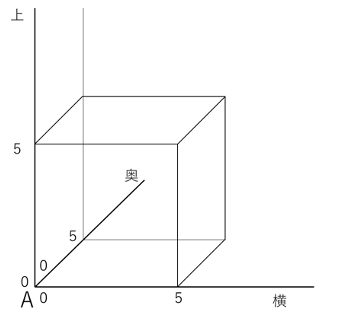
そして、立方体の頂点や辺、面の上にある点の位置を、
（Aから何ｍ横か、Aから何ｍ奥か、Aから何ｍ上か）で表すことにします。
例えば、B～Hの位置は
B（ 5 , 0 , 0 ）　C（ 5 , 5 , 0 ）　D（ 0 , 5 , 0 ）
E（ 0 , 0 , 5 ）　F（ 5 , 0 , 5 ）　G（ 5 , 5 , 5 ）　H（ 0 , 5 , 5 ）
と表せます。

STEP１　光の射しこむ方向を求める
今、面ABCD上に台形の光が当たっています。これが窓穴２から入った光だとすると、
窓穴の縦の辺はEHに平行なのに、床の光の左端の線はEHと平行ではないため、おかしいことになります。よって、床の光は窓穴１から入ったものとわかります。

窓穴１の４隅の点をI、J、K、L、床の光の２点をM、Nとします。

窓穴よりも床の光が右側に来ていますので、光は窓穴１より左の方向から射しています。
よって、MはIを通った光、NはLを通った光と考えられます。
　Iの位置は（ 1 , 0 , 1.5 ）　Mの位置は（ 2.5 , 1.5 , 0 ）
ここから、光の射し方は、
「横に1.5ｍ進むと、奥にも1.5ｍ進み、下に1.5ｍ下がる」
と求められます。それぞれの長さは比例しますので、
「横に〇ｍ進むと、奥にも〇ｍ進み、下に〇ｍ下がる」のが光の道筋です。
これをL→Nで確かめます。
Lの位置は（ 1 , 0 , 3.5 ）　Nの位置は（ 4.5 , 3.5 , 0 ）であり、
確かに「横に3.5ｍ進むと、奥にも3.5ｍ進み、下に3.5ｍ下がる」となっています。

STEP２　窓穴１から入った光が、側面に当たる部分を求める
光の道筋が分かったので、残りの頂点J、Kを通った光を考えます。
Jの位置は（ 4 , 0 , 1.5 ）です。この光は、側面BCGFに当たります。
Jを通った光が側面BCGFに当たる点をOとします。
側面BCGFはAから横に5ｍのところにあるため、Oの位置は（ 5 , ? , ? ）となります。
するとJからOは横に1ｍ進んだので、奥にも1m進み、下に1m下がることになります。
そこからOの位置は、（ 4+1 , 0+1 , 1.5－1 ）＝（ 5 , 1 , 0.5 ）となります。

同様に、Kを通った光が側面BCGFに当たる点をPとすると、
Kの位置は（ 4 , 0 , 3.5 ）、Pの位置は（ 5 , ? , ? ）で1ｍ動いていますので、
Pの位置は（ 4+1 , 0+1 , 3.5－1 ）＝（ 5 , 1 , 2.5 ）となります。

この2点を解答用紙の図に加えます。
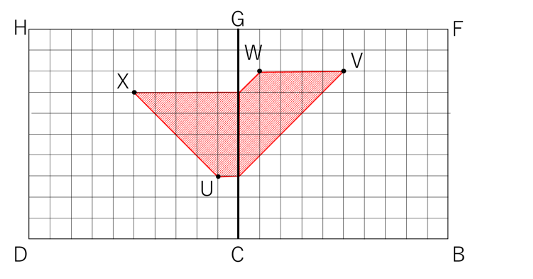
窓枠１の辺はそれぞれ、IJ→MO、JK→OP、KL→PN、LI→NMとなります。
MからOに向かう直線は、辺BCのところで折れ曲がることに注意しましょう。

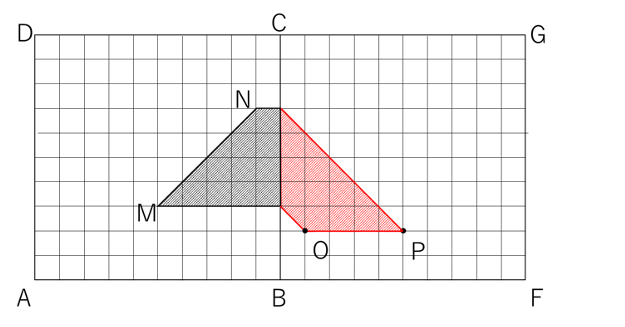
STEP３　窓穴２から入った光が、側面に当たる部分を求める
ここまで来ればもう少しです。光の道筋は同じなので、同じ作業を行います。
窓穴２の４隅の点をQ、R、S、T、それぞれが側面に当たる点をU、V、W、Xとします。

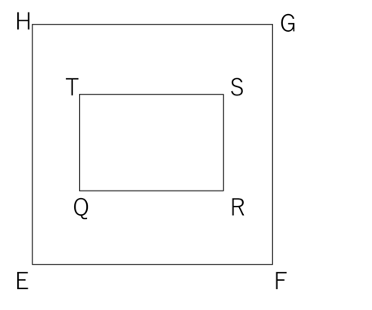
Q、R、S、Tの位置はそれぞれ
Q（ 1 , 1.5 , 5 ）　R（ 4 , 1.5 , 5 ）　S（ 4 , 3.5 , 5 ）　T（ 1 , 3.5 , 5 ）　です。

窓穴２から入った光は、側面CDHGか側面BCGFに当たります。
側面CDHGにある点は全て、（ ? , 5 , ? ）と表すことができ、
側面BCFGにある点は全て、（ 5 , ? , ? ）と表すことができます。

まず、側面CDHGに当たるかどうか考えます。
Q→UのUがCDHGにあるとすると、（ 1 , 1.5 , 5 ）→（ ? , 5 , ? ）より
3.5ｍ奥に移動したことになります。
そうするとUの位置は、（ 1+3.5 , 1.5+3.5 , 5－3.5 ）＝（ 4.5 , 5 , 1.5 ）になりCDHG上にあることがわかります。
R→Vの場合　（ 4 , 1.5 , 5 ）→（ ? , 5 , ? ）　奥に3.5m移動
Vの位置は、（ 4+3.5 , 1.5＋3.5 , 5－3.5 ）＝（ 7.5 , 5 , 1.5 ）となり、これは立方体の1辺5ｍを超えてしまいます。つまり、Rを通った光は側面CDHGには当たらないということです。
S→Wの場合　（ 4 , 3.5 , 5 ）→（ ? , 5 , ? ）　奥に1.5m移動
Wの位置は、（ 4+1.5 , 3.5+1.5 , 5－1.5 ）＝（ 5.5 , 5 , 3.5 ）となり、これもCDHGにはないことになります。
T→Xの場合　（ 1 , 3.5 , 5 ）→（ ? , 5 , ? ）　奥に1.5ｍ移動
Xの位置は、（ 1+1.5 , 3.5+1.5 , 5－1.5 ）＝（ 2.5 , 5 , 3.5 ）になりCDHG上にあります。

CDHGに点がないVとWはBCFG上にあることになります。
R→Vの場合　（ 4 , 1.5 , 5 ）→（ 5 , ? , ? ）　横に1ｍ移動
Vの位置は、（ 4+1 , 1.5+1 , 5－1 ）＝（ 5 , 2.5 , 4 ）になります。
S→Wの場合　（ 4 , 3.5 , 5 ）→（ 5 , ? , ? ）　横に1ｍ移動
Wの位置は、（ 4+1 , 3.5+1 , 5－1 ）＝（ 5 , 4.5 , 4 ）になります。

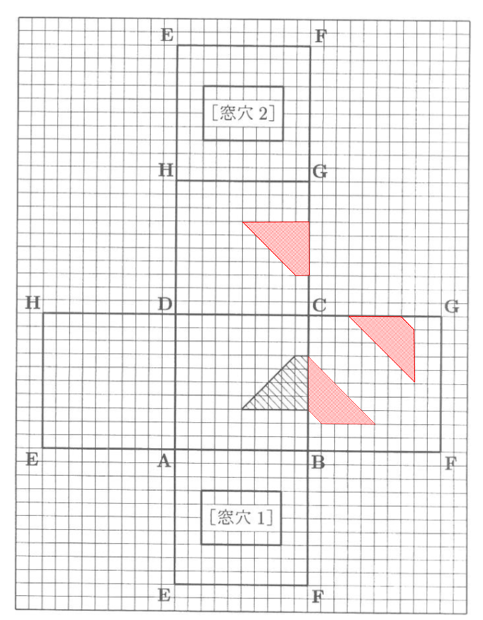
このU、V、W、Xを展開図に取り、UV、VW、WX、XUを結びます。
その時、一旦下の図のように、CDHGよBCGFをくっつけて作図するとわかりやすくなります。