算数の合否を分けた一題
海城中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| 1 | (1) A (2) A (3) A (4) A (5) A |
|---|---|
| 2 | (1) A (2) A |
| 3 | (1) A (2) A (3) B |
| 4 | (1) B (2) B (3) B |
| 5 | (1) B (2) C (3) B |
| 6 | (1) A (2) B (3) B |
A…海城中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題
出題総評
合格者平均/満点 = 88.5点/120点
受験者平均/満点 = 73.4点/120点
前半の大問1から大問3では平易な問題が並んでおり、ノーミスの受験生も多くいたものと思われます。基本的な解法を身につけて、ミスなく確実に解くことができた生徒は、高得点が取れるセットです。
後半は少し難度が上がりますが、明らかな捨て問というレベルのものはありません。全体的にしっかり手を付けて、確実に得点を重ねていくことが必要です。
問題文の意味が取りにくいところがあり、読解力で差がきそうです。問題文を読み取り、問題で問われていることの全体像をしっかり把握できる受験生に有利にはたらくでしょう。
問題別寸評
(1)計算
標準的な計算問題です。正解率も高く差はつかないでしょう。
(2) 食塩水の濃さ
濃さに分数が出てきますが、丁寧にやれば問題ないでしょう。
(3) 角度
基本問題です。確実に正解したいところです。
(4) 割合
ミスしないように慎重に解きましょう。
(5)面積
おなじみの典型題です。こちらも確実に正解したいです。
1から6が書かれた6枚のカードで3桁の整数を作ります。典型題で、かつ、ひねりが全くないので、ミスして失点しないように注意しましょう。
(1)
公式通りです。手早く正解しましょう。
(2)
百の位が6、5の数字はそれぞれ20個あるので、大きい方から50番目の数字は、百の位が4の数の中で大きい方から10番目の数字であることがわかります。
百の位が4の数20個中10番なので、百の位が4の数の中央付近を下の図のように書き出して調べると早いでしょう。
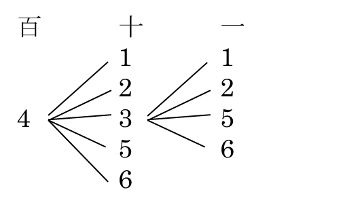
(3)
各位の数字の和=3の倍数を満たす数を調べます。
どの場合も異なる3数の並べ方になるので、同じパターンで数えやすいです。
三角形を分割して、面積比を考えます。難度がかなり抑えられている印象です。取りこぼし厳禁でしょう。
まず問題文からヒントを読み取ります。
同時間の距離比、A:B=800:750が分かるので、速さ比=16:15、時間比=15:16
を押さえます。
(1)
「初めてすれ違ってから40秒後に再びすれ違いました」
とあります。落ち着いて読めば、1回目の出会いにも40秒かかっていることに気づけるのですが、情報の出し方が絶妙で、翻弄された受験生も多くいたのではないでしょうか。
(2)

(3)

→【合否を分けた一題】で解説します。
3点で定められる平面による立体の切断です。勉強してきた原則に則って切断面を書きましょう。切った後、分けられた立体をどのようにとらえていくかがポイントとなります。
(1)三角柱
図のような切断面となります。求める立体は三角柱です。
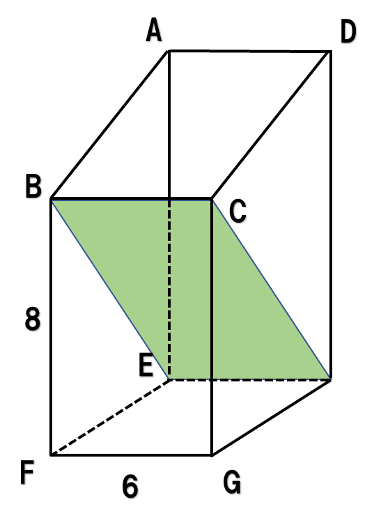
(2)四角柱の一部
図のような切断面となります。求める立体は高さ=10㎝の四角柱を斜めに切って2等分したものになります。これに気づけばほぼ即答できるのですが、どうでしょうか。面ABCDが斜めになっているせいで気づきにくくなっています。切断面を延長すれば、三角すいを用いたやり方が見えてきます。確かに馴染みの深い方法で、もちろん答えは出せますが、計算量は雲泥の差と言えます。
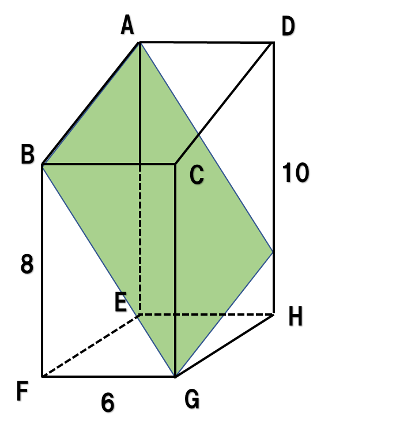
(3)三角すい台
直線ABと直線EFを延長して交わる点をとり、その点とHを直線で結べば三角すいができます。
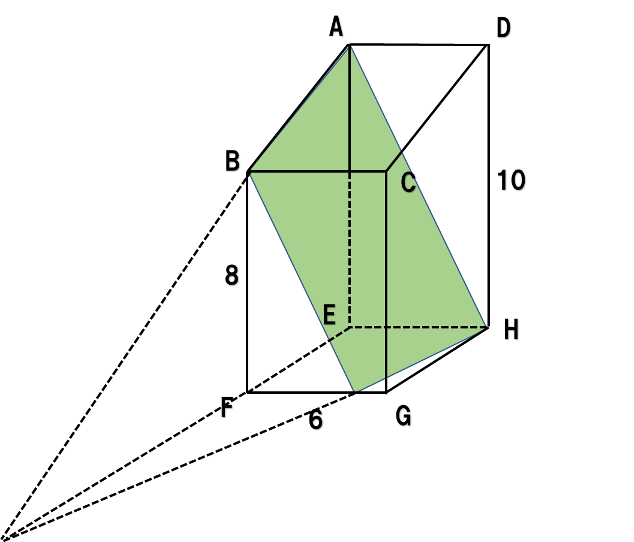
三角すい台の体積は
・大きな三角すい ― 小さな三角すい
・体積比
のいずれかの方法で求めましょう。
合否を分けた一題
普段「地球設定」で使っている時計やカレンダーを「異星設定」で運用する問題です。
変化のつけ方としては、もはや定番といってもよいのですが、変化への対応力、柔軟性が必要となってしまうので、本問で合否を分ける差がついた可能性は高いでしょう。
まず問題文ですが、
「ある星では、1日が8時間で、1時間が40分です」とあります。混乱なく読めたでしょうか。1日が8時間といいながら、その1時間の長さが異なっていて、読む段階で迷いが生じます。簡単なものでも、言い回しや条件提示の順序を変えるだけで、わかりにくさが倍増するのは算数ではよくあることですが、海城中はこれを意図的に、計算してやっているように思えます。
「異星設定」への対応
設定は異なりますが、時計の針が動く原理そのものは同じです。
いつもの問題(地球設定)と何が異なっていて、何が同じであるかを正確に見極める力が必要です。
問題文の条件を表にまとめると、このようになります。

問題文を読むだけでは分かりにくのですが、このように整理してみると、混乱なく取り組めると思います。
それでは「ある星」の設定で時計を動かしていきましょう。
(1)
時計の短針と長針のなす角を求めます。練習してきた解き方で、設定だけ変えて動かします。
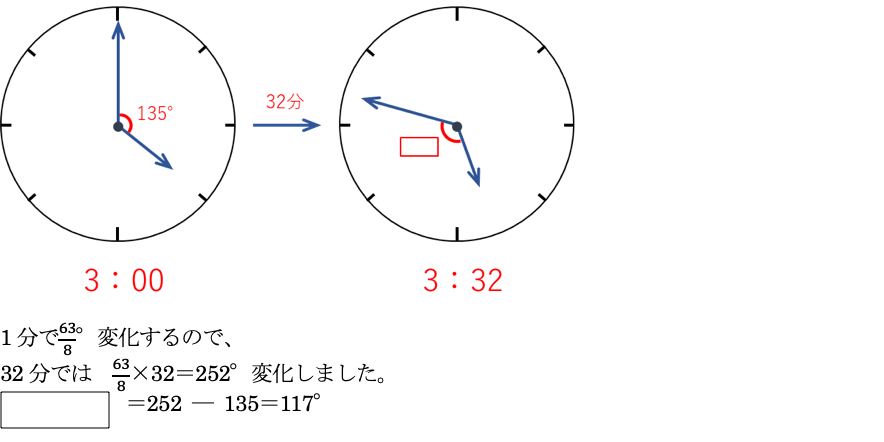
(2)
短針を追い越す前と後で、90°になることが2回ずつ起こりそうですが…
表にまとめていきます。

2時00分 は1時台と2時台の境目にあるため、1時台に90°となることは1回しかありません。同様に、6時00分は6時台に入るため、5時台も1回。よって、合計=14回。
一番確実なのは、すべての場合を図に書いてみることです。書き出す作業に関しては、この(2)は、設定のちがいにあまり影響されないことがわかります。だだ、この設問自体丁寧な作業を必要とするため、正解率は低いものと思われます。
(3)
4時16分の次に角度が128°になるのは、下の図のような時です。この時刻を求めて、4時16分の何分後になるかを答えればよいのです。
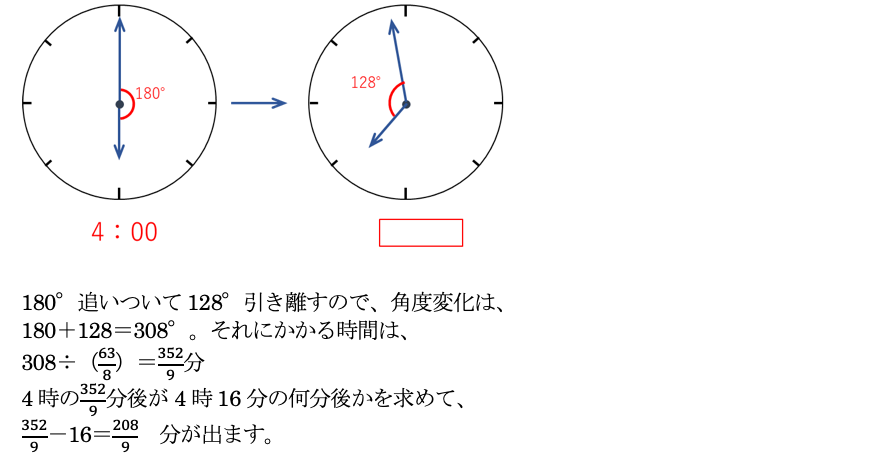
(2)は地球設定でもやや面倒な問題ですが、設問パターンとしてはどれも「地球上で」見慣れた問題のはず。この星の設定に順応して時計をうまく動かすことができた受験生は、やることは同じなので、楽に攻略できたのではないでしょうか。