算数の合否を分けた一題
海城中入試対策・算数の合否を分けた一題(2019年度)
難易度分類
| 1 | (1) A (2) B (3) A (4) A (5) A |
|---|---|
| 2 | (1) A (2) A |
| 3 | (1) A (2) A |
| 4 | (1) A (2) C |
| 5 | (1) B (2) B (3) C |
| 6 | (1) A (2) A (3) C |
A…海城中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、得点差がつかない問題
出題総評
合格者平均/満点 = 88.5点/120点
受験者平均/満点 = 75.3点/120点
全体としては、かなり平易な問題が並んでいます。
終盤の5、6で大きく差がついたのではないでしょうか。
問題別寸評
(1)計算
計算の工夫ができそうなことがすぐにわかるので、筆算を始めることはまずなさそうです。
(2) 食塩水の濃さ
濃度1.5倍とあります。天秤図などを用いて条件をうまくまとめないと厳しい問題です。
海城中の濃度の問題は難しめのものが多いので、濃度の問題で設定が難しそうと感じたら、後回しにすることも考えてよいでしょう。
(3) 流水算
最も基本的な形です。確実に得点しましょう。
(4) 面積
斜線部分と網掛け部分を比べます。
| 斜線部分 | 網掛け部分 | |
|---|---|---|
| 面積比 | 1:1 | |
| 一周全体の面積比 | 3:1 | |
| 中心角 | 1:3 | |
より、斜線部分2か所の中心角の和=90°が求められます。この問題は軽快にさばかないと時間を取られるかもしれません。
(5)平面図形
GとHが辺BC、CDの中点になっていることにすぐに気づけるでしょうか。これに気がつけば三角形EBGと三角形FHDの割合が等しいこともわかります。
三角形EBGの割合のみを求めるという方針が立てば、その先は容易でしょう。
大小2つのサイコロを使ってコマを進めます。
(1)
和=3,7,11の場合を調べます。
(2)
Aに来る → 積=4の倍数
Cに来る → 積=4の倍数+2
ですが、言い換えると
積=偶数の場合を求めることになります。
調べ方については、2つのサイコロの場合は以下のような対照表を書いて、全体像を見ながら作業をすると安全です。
≪和の表≫

≪積の表≫

(1)は3,7,11に印をつけます。

印の個数を丁寧に数えましょう。
(2)は偶数に印をつけてもよいのですが、奇数のほうがチェックしやすそうなので奇数に印をつけました。

全個数から奇数の場合を除いて、36-9=27と安全に求めることができました。
答えが必ず出る問題なので、いかにミスをしない方法をとるかが重要です。
立体の問題としては、海城中の問題なのかと思うほど、難しくない問題になっています。差がつきにくかったのではないでしょうか。
(1)
QPに平行な線を面AEHDに引いて終了です。
(2)
Pより上の部分、つまり立方体の上半分が合同切断になっていることがすぐにわかります。
したがって、切断面が立方体を1:3に切断していることがわかってしまいます。
計算間違いに注意しましょう。
円の通過領域の面積を求めます。
(1)
手数がかかる問題です。いかにミスをしないかが試されます。
・丁寧に作図する
・部品に分ける
・集計する(計算は慎重に)
作図の要領で処理時間の差が出そうです。
(2)
円全体を動かすのですが、わかりやすくするために、円周上の1点に注目してみましょう。
まず大円Qの中心を点Oに固定します。
次に円Q上の1点に着目します。中心を円Oの内部で自由に動かすと、Q上の1点も連動して同じ大きさの円を描きます。円Qの周上の全ての点が同様に半径=1の円を描くと考えると、幅=2㎝の「ドーナツ型」が求めるべき領域であることがわかります。
一般にこのタイプの問題では、動く図形が通過できない内側の領域の把握が不十分になりがちです。
この(2)でも、外側の境界はすぐわかりますが、内側の通過できない領域の把握が難しく、受験生にとっては対応しづらかったのではないでしょうか。
下手に図を描くよりも、手で輪っかを作って、その中心が円Oの周上を一周するように動かしてみると、案外早くイメージがつかめるかもしれません。
→【合否を分けた1題】で解説します。
自分自身以外の約数の和を約束記号[ ]で表します。
(1)ルール運用の練習問題
ミスには注意しなければいけませんが、単なる肩慣らしではありません。
後に続く(2)(3)に対してどのような布石になっているかを後で考える必要があるかも知れません。
このことを見越して、敢えてていねいに書き出しておきましょう。
[1]=0 ←ここは要注意。
[2]=1
[3]=1
[4]=1+2
[5]=1
[6]=1+2+3
[7]=1
[8]=1+2+4
[9]=1+3
[10]=1+2+5
(2)
自分以外の約数の和=1を満たす整数なので、素数を考えればよいことがわかります。作業を通して気づけるようになってはいますが、それ以前に気づいてしまうはずです。
(3)
x=7, y=8 という例からどこまで読み取れるか、が勝負です
この例からは
・xが素数
・[y]=y-1
となっていることがとりあえず読み取れますね。
ここから100以上の素数の前後を即調べにかかることもできるでしょう。
その前にyについてもう少し考えてみます。
[8]=1+2+4
よく見ると、x=7, y=8よりもっと前に、条件を満たす連続2数が出てきていますね!
x=3, y=4
がそうです。
[4]=1+2 になっています。
このあたりで共通点を考えて…
yは2の累乗数(2を掛け合わせてできる数)かな?
と察しがつけば、求める範囲内では
y=128しかありません。果たして、その前の数127は…素数になっています。
気づけば近くにあるゴールでしたが、どこまで見通せるかで処理時間が全く違ってきます。先述のとおり、調べる量が多くなったとしても、答えに到達することは十分可能なので、たとえ道筋がうまく見えなくても、うまくいかないなりに執念でゴールまでたどり着きたいところですね。
合否を分けた1題
算数の問題文中ではあまり見かけない接続詞「しかし」が登場します。
まず問題文ですが、読解に手間がかかるように設定されています。
「16秒多くかかった」とありますが、何に対して16秒多くかかったのかが書かれておらず、考えなければいけません。「予定の速さで注水し続けた場合に比べて」16秒多くかかっていることを早めに見抜きたいところ。
着眼点の一例ですが、接続詞「しかし」に注目してみます。
水を入れることにしました。→ しかし → 水の出が悪くなった
とあります。
「しかし」の前の内容は、悪くなった、の逆なので、水の出が良かった、すなわち
「予定の速さで」水を入れることにしました、と考えることができます。これで、
「予定の速さで注水し続けた場合に比べて」16秒多くかかっていることが理解できるでしょう。
ここからはお約束通りに攻めていきます。
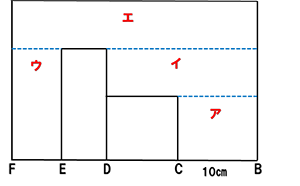
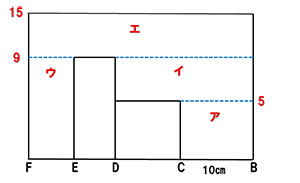
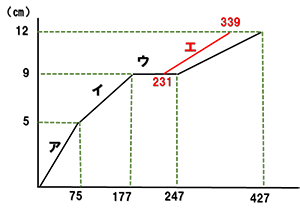
図のように注水部分をア~エに区分します。注水すると
ア→イ→ウ→エの順に水が入っていきます。奥行きの長さは与えられていませんが、この手前の面上で考えます。
(1)
アの部分に75秒、イの部分に102秒かかっています。よって、この注水時間の比がアとイの体積比(正面から見た面積比)となります。また、グラフからア、イの高さがわかっていますから、
| ア | イ | |
|---|---|---|
| 体積 | 75:102 | |
| 高さ | 5:4 | |
| 底面積 | 10:17 | |
BC:BD=10:17より、BD=17㎝が求められます。
(2)
16秒多くかかったとあるので、
ウの部分を満たすのにかかる時間は、
70-16= 54秒の予定だったことがわかります。グラフから、アを満たすのに75秒かかっていることはわかるので、
アの体積:ウの体積=75:54
体積比と高さ比がわかったので、底面積=横の長さの比を求めます。
| ア | ウ | |
|---|---|---|
| 体積 | 75:54 | |
| 高さ | 5:9 | |
| 底面積 | 5:2 | |
BC: EF=5:2より、EF= 4㎝が求められます。
(3)
問題文を丁寧に読んでいきましょう。
ウの区間内で注水速度が変化しているので、エの区間では変化後の注水速度で注いでいることがわかります。
エの区間に注目します。
容器が満水になる時刻が予定より88秒遅れたとあるので、終了予定時刻は339秒後です。また、ウに注ぎ終わる予定時刻=エに注ぎ始める時刻が予定より16秒遅れていますので、その予定時刻は
247-16=231秒後です。このことから、エの部分に注水する予定の時間は、
339-231=108秒だったことがわかります。
この状況をグラフに書き込むとこのようになります。
| 予定 | 実際 | |
|---|---|---|
| 注水時間 ↓(逆比) |
108秒 | 180秒 |
| 注水速度 | 5 : 3 | |
注水速度が5から3に変化したことがわかりました。
それではいよいよウの区間を攻略しましょう。
もし注水速度=5で注ぐと、
231-177=54 秒かかっていたことがわかります。これを用いてウの区間の体積を
5×54=270 と表します。
実際には途中から注水速度を3にしたので、かかった時間が
247-177=70秒になりました。
「速さ=5と、速さ=3 で合計70秒かけて、270の水を注いだ」
これで、つるかめ算を解く準備ができましたね。
なお、この手の問題に答える際には「起点」を必ず確認しましょう。本問では「水を入れ始めてから」とあるのを見逃さないようにしてください。
さて、この問題の難しさですが、
「88秒多くかかった」
「水の出が悪くなった」
など、一読しただけでは意味が取りにくいところが何か所かあります。
「88秒多くかかった」 → 「予定より88秒多くかかった」
「水の出が悪くなった」 → 「注水速度が変化した」
など、あいまいにぼかされた情報を正確にキャッチできたでしょうか。
ウの予定時間とエの予定時間が確定するまでにどれくらいかかるか、読解力で相当差が付きそうな問題です。
情報を確定させてしまえば、知っているやり方に結び付けるのは難しくないと思われます。
速さが変化→つるかめ算かな、と瞬時に反応できるように、対応力を高めておきましょう。
海城中入試対策・関連記事一覧
海城中入試対策・同じ教科(算数)の記事
海城中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)