算数の合否を分けた一題
海城中入試対策・算数の合否を分けた一題(2018年度)
難易度分類
| [1] | (1) A (2) A (3) ①A ②A (4)①A ②A |
|---|---|
| [2] | (1) A (2) A |
| [3] | (1) A (2) A (3) B |
| [4] | (1) B (2) B (3) B |
| [5] | (1) B (2) C |
| [6] | (1) A (2) B |
A:海城中学合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度・処理量から判断して、得点差がつかない問題
出題総評
大問6題、小問18題という問題構成であった。大問1~大問3までは海城中学合格を目指す受験生にとっていずれも正解できなといけない問題であった。この前半部分をいかに正確さとスピードをもって解答できたかが重要なポイントである。算数の合格者平均点を取るためには前半部分の大問1~大問3でミスを1問以内に抑えて、後半部分の大問4~大問6で半分を正解する必要があったと思われる。
問題別寸評
(1) 四則計算 (2)過不足算 (3)規則性〔おまけの問題〕 (4)平面図形
いずれも見たことがある解き慣れた問題だったのではないでしょうか。
全問正解することが望ましい。
ダイヤグラムなどを利用して一郎君と花子さんの動きを整理すれば容易に求めることができたのではないでしょうか。
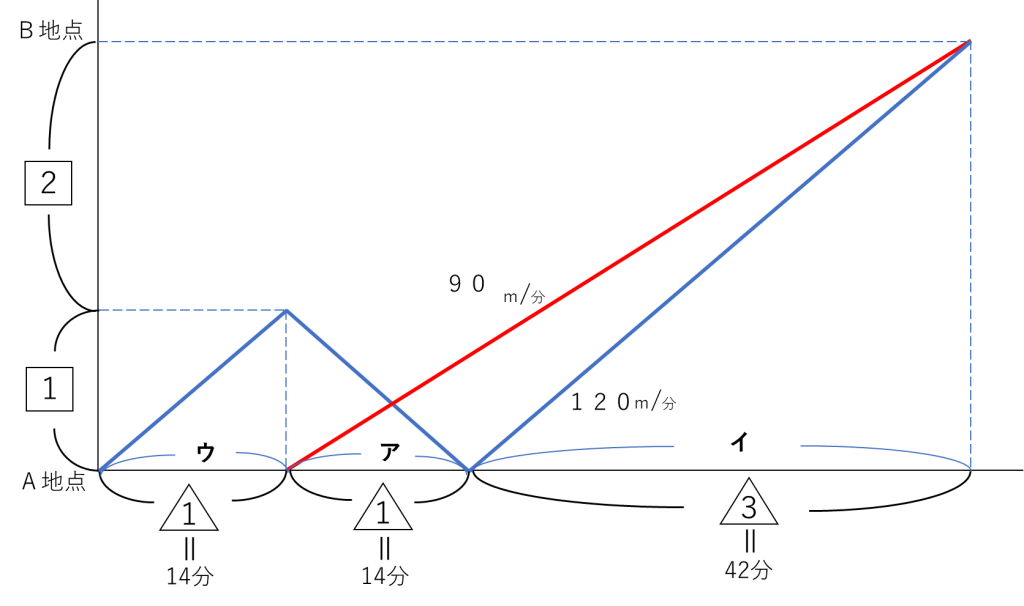
一郎君と花子さんの速さの比が3 : 4だから、かかる時間の比は 4 : 3 である。
つまり、 (ア+イ) : イ = 4 : 3 ということになる。
よって ア : イ = 1 : 3 とわかる。・・・・①
また、進んだ距離が 1 : 3 なので ウ : イ = 1 : 3・・・・②
① ②より、ア : イ : ウ = 1 : 1 : 3 だとわかる。
花子さんがA地点に戻りはじめたとき、一郎君はA地点を出発したことになる。
ウの時間が14分だから ア=14分 イ=42分
(1)A地点からB地点までの距離は 毎分120m×42分=5040m
5040m
(2)120×14÷(120+90)=8分
8分
(1) 12の約数 1,2,3,4,6,12 の逆数の和です。
(2) (1)の計算を見てみる
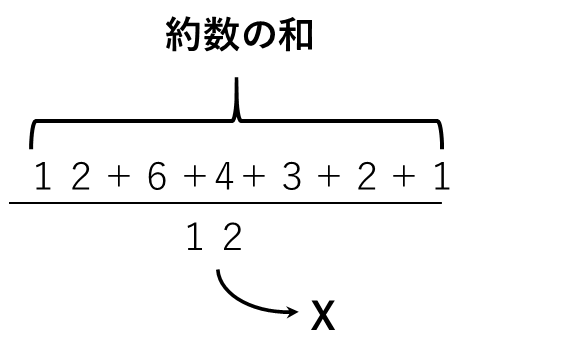
と表せるので

となります。
よって、求めるある数Xは
X=2016
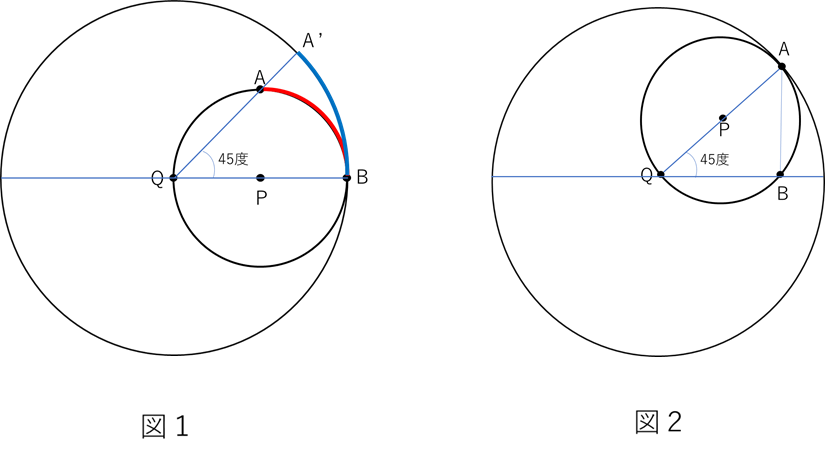
(1) 図1で弧ABと弧A’Bの長さは同じ
になりますので、
点Aは点A’の位置に移動します。そのときAPはQA’上にあるので、図2のように円Pは移動します。
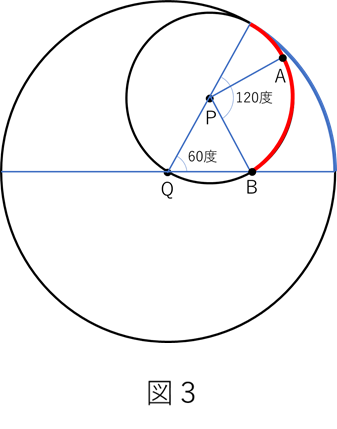
(2) 角CQP=60度になるまで転がしたとき、円Pは図3のように移動する。
円Qの60度分の弧の長さは、円Pの120度分の弧の長さに等しい。
このとき、三角形BPQは正三角形になる。
よって角BPQの大きさは、60度になる。
60度
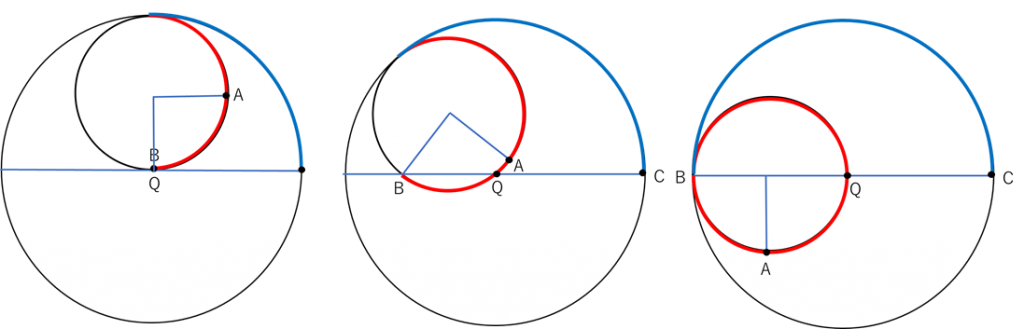
(3) 円Pが円Qの内側を半周したとき、点A,点Bの位置ははじめの状態に戻りますので
円Pがあと半周する時も点Bは直径の上を移動することがわかります。
8cm
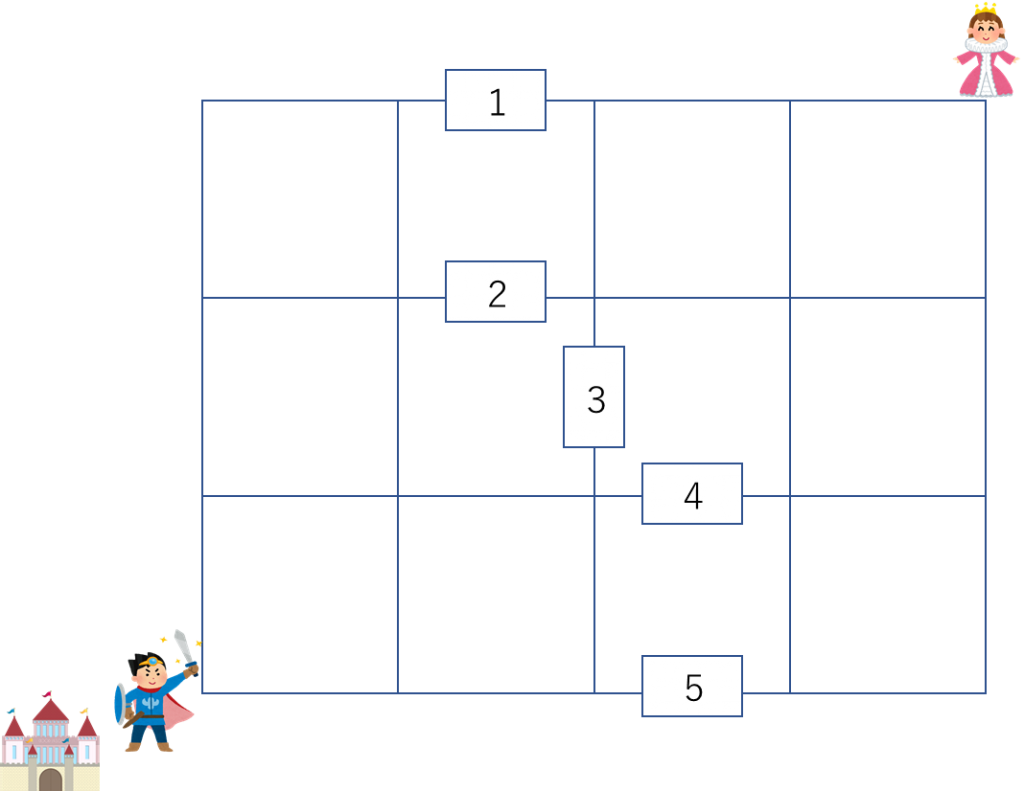
(1) 行きに1番の橋を使う場合、行きは4通り、帰りは31通りですから、
4×31=124通り。
行きに2番の橋を使う場合、行きは9通り、帰りは26通りですから、
9×26=234通り。
行きに3番の橋を使う場合、行きは9通り、帰りは26通りですから、
9×26=234通り。
行きに4番の橋を使う場合、行きは9通り、帰りは26通りですから、
9×26=234通り。
行きに5番の橋を使う場合、行きは4通り、帰りは31通りですから、
4×31=124通り。
124×2+234×3=950
950通り
(2)

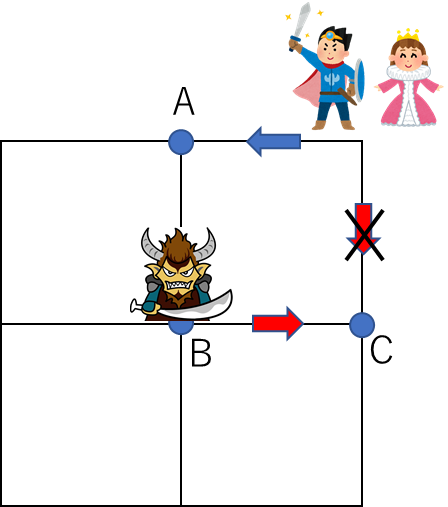
勇者が道を7つ進んだとき点Pまたは点Sに、魔王は点Bにいます。
このとき勇者が点Pにいると、勇者が次の道を1つ進むとき、点Aで魔王と出会うことになります。
よって勇者が姫に出会うまでに点Pを通ることはできません。
勇者が道を6つ進んだとき点Qまたは点Rに、魔王は点Cにいます。
このとき勇者が次の道を1つ進むと、勇者は魔王と点Bで出会うことになります。
よって勇者は姫に出会うまでに点Qまたは点Rを通ることはありません。
以上より、勇者は姫に出会うまでは点Sを通ることがわかります。
次に、勇者が姫に無事出会うことができて、お城まで戻ってくる場合を考えます。
勇者は姫に出会ったとき、9つの道を進んだことになります。このとき、魔王は点Bにいます。
勇者は魔王と出会うことがないように進むので、もう1つ道を進むとき勇者は点Aに進むことしかできません。
さらに、もう1つの道を進むとき、勇者は点Bに進むことはできません。
よって、点Pからお城に戻ることになります。
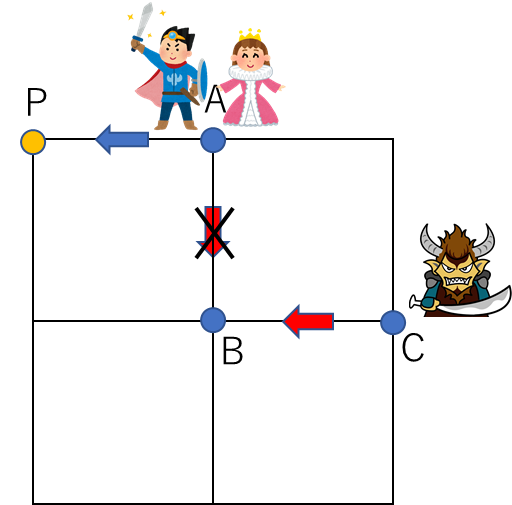
以上より、勇者が点Sまで行く方法が21通り、点Sから姫に出会うまで1通り、姫に出会ってから点Pまで1通り、点Pからお城まで行く方法は35通りありますので、
21×1×1×35=735通り
735通り
【合否を分けた一題】
近年、男子難関校は立体の切断の出題が当たり前のように定着してきています。したがって受験生も十分な対策を行い受験に臨んでいることと思われます。今年度の海城中の出題も立体の切断の仕方は受験生にとって比較的慣れ親しんでいるものだったのではないでしょうか。しかし、【6】という最後の問題での出題であったため、時間的にゆとりをもって考えることができなかった受験生もいたのではないでしょうか。そういった意味で合否を分けた一題といえるでしょう。

(1) 三角形ABM、三角形APB、三角形BPMは相似の関係にあるので、AP:MP=4:1となります。△PBMの面積は7.2㎠ だから、△ABMの面積は36㎠となります。
よって正方形の面積は144㎠とわかるので、正方形の1辺の長さは12㎝となります。
12㎝
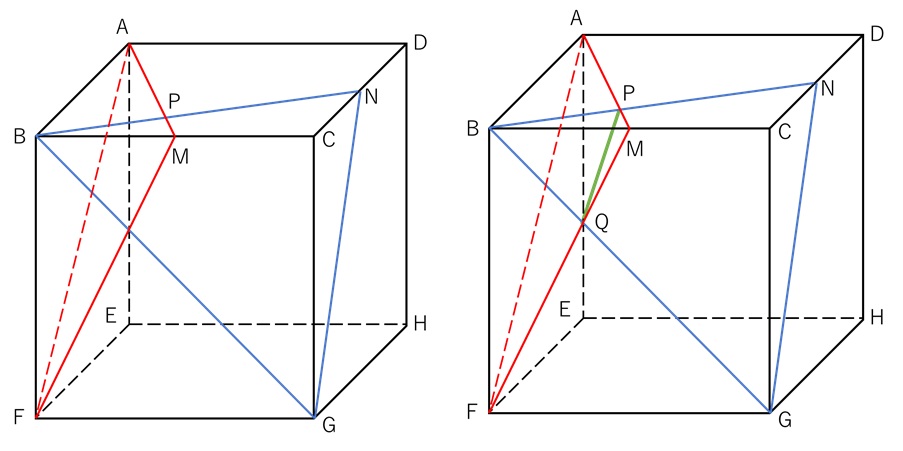
(2) 立体を平面で2回以上切断する問題は、切断面の上に新たにできる交線をいち早く作図することがポイントになります。交線を引かなければ新しくできた立体の形が把握できないことが多いのです。一方、交線を引くことができれば新しくできた立体の形が把握しやすくなります。
上の右の図は交線となるPQをひいた図です。すると、三角すいQ-PBMが存在することに気づくでしょう。実はこの三角すいが赤い切断面で切断した三角すいF-ABMと青い切断面で切断した三角すいG-BCNの重なっている部分になっています。

全体の立方体-(三角すいF-ABM + 三角すいG-BCN - 三角すいQ-PBM)
=1728-(144+144-9.6)
=1728-278.4
=1449.6
1449.6㎤
海城中入試対策・関連記事一覧
海城中入試対策・同じ教科(算数)の記事
海城中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)

 (5 votes, average: 4.60 out of 5)
(5 votes, average: 4.60 out of 5)