算数の合否を分けた一題（2017年度）

算数の合否を分けた一題

海城中入試対策・算数の合否を分けた一題（2017年度）

難易度分類

[１]	（１）A　（２）A　（３）A　（４）A　（５）A
[２]	（１）A　（２）B
[３]	（１）A　（２）B　（３）C
[４]	（１）A　（２）A　（３）A
[５]	（１）A　（２）A
[６]	（１）A　（２）B　（３）C

Ａ：海城合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題

出題総評

今年は、全体的な内容としては例年よりも易化していました。大問１は5問の小問集合、大問２は和差の問題、大問３は数表を使った規則性の問題、大問４はくるった時計をテーマにした通過算の問題、大問５は図形の移動とグラフの問題、大問６は立体図形の求積の問題という構成でした。

問題別寸評

［１］

（１）答　１７

分数と小数の入り混じった計算問題。途中の計算や、答えも複雑な形にはならないので、落としてはいけない問題です。

(２)答　２：３

濃度の違う食塩水の混合の問題。塩の量を計算することができないので、本校を受験する生徒としては、面積図や天秤を使うということにすぐ気づかなくてはいけない問題です。

(３)答　７１°

長方形の折り返しによる角度の問題。対頂角の知識・折り返した後の角度は折り返す前と同じ角度になっていることを使う問題です。

(４)答　晴3日　くもり7日　雨1日

雨の日を①日、晴れの日を③日とおいて、売れた本数をもとに不定方程式に持ち込む問題です。本校を受験する生徒は、この問題も正解したいところです。

(５)答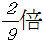　

三角形の中に、さらに三角形をいれた平面図形の問題。全体から周りの三角形を引いて考える知識は、確実に・すぐ使えるようにしておかなくてはならない問題でした。

２

(１)答　7人

表かベン図を描いて、Aの合格者数と不合格者数、Bの合格者数と不合格者数を整理していく問題です。確実におさえておきたいところです。

(２)答　5人

少し複雑な設定になってはいますが、Aを80点以上で合格した人数と60点以上で合格した人数、Bの合格者数と不合格者数とで再度ベン図や表を描き、状況の整理をしていく問題です。先ほどの問題で表やベン図を描いたので、その後でどのように既に描いてある図に整理をするのか？と戸惑った受験生も多いのではないかと思われます。

３

(１)答　２２

典型的な、平方数に着目して考えていく数表の問題。数の動き方にも注意しましょう。

(２)答　３・７・１３・２１・３１・４３

表に書かれている数をもとにして、どのような時にアの方が小さくなるのか、位置の規則を掴むことが出来たかどうかが分かれ道でした。

(３)答　４４個

（２）の続きになりますが、対角線上の数に着目する、ということに気付けた受験生は増える数の規則にも着目できたことでしょう。ただ、増える数が４，６，８，１０…とさらに２ずつ増えていく規則に気付けても、どこまで足したら２０１７以下になるか、というところについてはある程度の数のセンスと緻密な調べ上げが必要になってきます。ここで時間を浪費してしまっては、後半の問題に手が出せなくなるので後回しにすべきでしょう。

４

(１)答　２４．５秒

正しい時間を含め、時計が３種類ある問題です。くるった時計というテーマに、さらに通過算の要素も加わった少々珍しい問題です。

(２)答　２９７ｍ

電車同士の追い抜きが絡んだ単純な通過算の問題ですが、はじめにくるった時計から正確な時間に直す必要があることに注意が必要です。

(３)答　８秒

こちらも、電車同士の出会いが絡んだ単純な通過算の問題ですが、最後に正確な時間からBの時間へと直す必要があることに注意が必要です。

５

(１)答　①８．６４　②２６

２つの三角形があり、片方の三角形を移動して、両者の重なった面積をグラフから読み解いていく問題。①については、重なった部分で直角三角形相似が使えることに気付けたかがポイントです。②については、グラフを見て変化の起こっている各部分が、それぞれどのような重なりになっているのかを整理できれば、PQの長さが分かって答えにたどり着けたことでしょう。

(２)答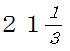　

２２秒後の重なりを実際に作図し、ピラミッド相似が使えることに気付ければ正答できたと思われます。

６

(１)答　３：２０

たて、横、高さがそれぞれ全体のどれだけになっているかが、問題文で明らかにされているので確実に出来なくてはいけない問題です。

(２)答　１３．８㎠

立体のままでは拉致があかないので、まずは上から見た平面図（BCD・IJK）を描きましょう。そのうえで、AR：RD=３：２であることと、AP：PB=１：１であることをピラミッド型の相似としてとらえることによって、各々の長さを求めることが出来ます。

(３)答　５１．５２㎤

断頭三角柱であることに気付けたかどうかが、完全に正誤の分かれ目です。高さがそれぞれ、４ｃｍ、４ｃｍ、３．２ｃｍですので、その平均値を先ほど（２）で求めた底面積にかければ答えが求まります。

合否を分けた一題

今年の海城中の算数は、去年と比較すると全体的に取り組みやすかったと言えますが、それでも大問３の（３）や大問６の（３）といったような難問も存在しました。大問３でいかに時間を消費せずに、大問４や５を取りこぼさなかったか、という一点が合否をわけたと言えるでしょう。大問４のくるった時計の係わる通過算の問題を取り上げます。

［４］くるった時計・通過算
（１）
正確な時間が計れるA、くるっているBとCの速さを較べます。問題文の３行目から、秒単位でA：B：C=６０秒：６４秒：５６秒＝１５：１６：１４です。問題文の６行目から、Bで２８秒なのでCでは２８÷１６×１４＝２４．５秒となります。
答え：２４．５秒

（２）
ここから、通過算が係わってきます。Bで２８秒かかったので、正確な時間（A）では２８÷１６×１５＝２６．２５秒になります。普通電車と急行電車の速さが時速で与えられているので、秒速に直すと普通電車は９０÷３．６＝２５ｍ、急行電車は１２６÷３．６＝４５ｍになります。電車同士の追い越しなので、（４５－２５）×２６．２５＝５２５ｍが普通電車と急行電車の和となり、急行電車の長さは５２５－２２８＝２９７ｍとなります。
答え：２９７ｍ

（３）
今度は電車同士の出会いなので、（２２８＋２９７）÷（４５＋２５）＝７．５秒となりますが、これは正確なストップウォッチ＝Aで計測した場合の時間です。よって、Bに直すと７．５÷１５×１６＝８秒となります。
答え：８秒

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？