理科の合否を分けた一題（2020年度）

理科の合否を分けた一題

海城中入試対策・理科の合否を分けた一題（2020年度）

難易度分類

１	問１　A　　問２　A　　問３　B　問４　Ａ　　問５　B
２	問１　A　　問２　A　　問３　A　問４　Ａ　　問５　B
３	問１　A　　問２　B　　問３　A　問４　Ａ　　問５　A　　問６　C
４	問１　B　　問２　A　　問３　A　問４　Ａ　　問５（１） C　　（２） C

A…海城合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

2020年度の海城は、幅広い知識を駆使して解答する問題と、リード文を読み取って論理的に考える問題が特徴的です。
45分80点満点で、受験者平均は46.8点（昨年度47.2点）とやや下がり、合格者平均は52.4点（昨年度51.5点）と上がっています。おそらく、２極分化が進んでいる結果と思われます。上位分布にくいこむためには、難易度の高い問題を一題でも多くクリアしておかなければなりませんでした。

物理分野は、熱の伝わり方と気体の体積の変化についての問題。
化学分野は、塩酸と水酸化ナトリウム水溶液の中和についての問題。
生物分野は、植物のつくりと育て方についての問題。
地学分野は、堆積物の粒子の観察についての問題。

物理→化学→生物→地学　のならびは、例年通りです。
本年は、もともと多かった記述問題がさらに増え、そのなかには、手がかりがうすく、自身の知識とアイディアで書き切らなくてはならないものもありました。
リード文は相変わらず長文ですし、図や表も、初見で理解するにはかなり歯ごたえのあるものでした。その中で高得点をマークし、合格を勝ち取るのは容易ではありません。
対策としては、細かい知識であっても、取りこぼさずにおぼえること、知識の裏付けとなる考え方もセットにして身につけておくこと。実験手法やデータ処理に興味をもち、重点的に取り組んでおくことが挙げられます。

問題構成は、４分野から大問４題、小問42問。
解答形式は、記号選択が15問、言語が13問、記述が11問、数字が３問。総問数は昨年と同じですが、記号選択と数字が減って、言語と記述が増えています。
選択肢は、基本的な内容が大部分をしめますが、情報を整理し論理的に考えなければならない高レベルのものもありました。
計算は、大幅に減少していますが、つるかめ算を利用するものがありました。
記述は、2行程度が１問、１行程度が８問、８字程度のものが２問でした。

問題別寸評

１

（物理）熱の伝わり方と気体の体積の変化についての問題です。
熱の伝わり方の基本の知識が中心です。記述が３問あり、使える知識として身についているかどうかが問われます。対流に関連づけて、最後に気体の体積の変化に関する計算問題が配置されています。
リード文が長いのですが、記述のヒントが散りばめているので、ポイントをつかみながら読み取るようにします。

問１

熱の伝わり方には、伝導、対流、放射の３つがあります。魔法びんは、伝導と放射をさまたげることで保温するしくみになっています。伝導については、内びんと外びんの間を真空に近い状態にして、熱を伝える物質がない状態を作り出しています。

問２

魔法びんのガラス製の内びんには、金属のはく（アルミはくのようなもの）がはりつけられていて、金属光沢によって中に入れたものが出す放射熱を反射し、びんの内側にもどすはたらきがあります。現在使われている、保温性のある水筒の内側を見ると、白く光沢のある金属でできていますが、これもこの仕組みを利用したものです。

問３

冷暖房の効率を上げるために、窓わくやガラスにどのような工夫をすれば良いかを、記述する問題です。ここでは、読み進めたリード文の内容をふまえて答えると良いでしょう。図１から、窓わくを、熱が伝わりやすいアルミニウムから木材などに変えること。また図２を参考に、ガラスを２重にし、その間を真空にすることが考えられます。

問４

対流のメカニズムについて説明する文章の、空欄補充問題です。液体や気体は、温度が高くなると膨張して軽くなり、上に移動することで対流が起こることがわかっていれば解答できます。海城受験生なら、確実に得点できたのではないでしょうか。

問５

気体の膨張について、具体的に計算する問題です。気体はその種類にかかわらず、温度が変化すると、一定の割合で体積が変化します。たとえば、温度が１℃上がると、０℃のときの体積の273分の１だけ体積が増加します。この場合、割合で考えれば良いので、０℃の気体の体積を「１」とすると、—６℃の気体の体積は６℃分減るので、１—（1/273）×６＝267/273 です。また、30℃の気体の体積は30℃分増えるので、１—（1/273）×30＝303/273 です。同じ体積あたりの重さの比は、この体積の逆比になるので、—６℃の気体の重さ：30℃の気体の重さ＝303：267＝101：89です。

２

（化学）塩酸と水酸化ナトリウム水溶液の中和についての問題です。
オーソドックスな中和反応の問題です。
問１〜４までは確実に得点できるのではないでしょうか。問５もよく見かける問題ですから、ふだんから演習問題に慣れている生徒であれば、迷わず処理できたはずです。

問１

まずは基本の知識です。塩酸の溶質は気体の塩化水素です。

問２

塩酸の性質と、水酸化ナトリウム水溶液の性質について答える問題です。塩酸のみに当てはまるのは、酸性であること、マグネシウムと反応すること、石灰石と反応して二酸化炭素が発生することです。水酸化ナトリウム水溶液のみに当てはまるのは、蒸発させると固体が残ることです。両方に当てはまるのは、アルミニウムと反応すること、どちらにも当てはまらないのは、銅と反応することです。基本の知識ですから、ここうっかり失点しないように注意します。

問３

実験番号⑪の結果に着目します。水酸化ナトリウム水溶液Bのみ100g入っていて、残った固体Cが4.80gなので、水酸化ナトリウム水溶液Bの濃さは、（4.80/100）×100＝4.8（％）です。こちらも、難なくクリアできたのではないでしょうか。

問４

表から、完全中和するところにあたりをつけます。手がかりは、残った固体Cの増加量です。①〜⑥では、実験番号ごとに0.72gずつ増えていますが、⑥と⑦の間は0.32g、⑦〜⑪は0.22gずつです。したがって、⑥と⑦の間に中和点があることがわかります。
（１）実験番号②では、塩酸Ａが余るので、残った固体は塩化ナトリウム（食塩）だけです。
（２）実験番号⑩では、水酸化ナトリウム水溶液が余るので、塩化ナトリウム（食塩）と水酸化ナトリウムが残ります。
（３）問１の物質とは、塩酸に溶けている塩化水素のことです。中和反応では、水溶液中の塩化水素と水酸化ナトリウムが反応するので、塩酸が余る①〜⑥で、塩化水素が残っていると考えます。
（４）塩酸は酸性ですから、BTB溶液は黄色になります。

問５

中和点は⑥と⑦の間です。つるかめ算を使って計算します。
⑥までは、塩酸が１g増えるごとに固体Cは0.072g増え、⑦以降は0.022gずつ増えていることから、（0.32—0.022×10）÷（0.072—0.022）＝２（g）より、塩酸Ａが、50—２＝48（g）のとき、完全中和するとわかります。

３

（生物）植物のつくりと育て方についての問題です。
前半は、家庭菜園で育てる野菜の種類とつくりのちがいについてのかなり細かい知識と、さらに苗ポットにまいた種の配列を推測する問題。後半は、ジャガイモとサツマイモの成長の仕方のちがいと育て方のちがいについて考える問題です。どちらも、基本の知識を確かめる問題から、さらに、設問に対して答えるべきことがらを論理的に考えて、対応する問題へ進展する構成です。

問１

トマト、キュウリ、ナスは双子葉類、トウモロコシ、ネギが単子葉類です。ひげ根は、単子葉類の特徴ですから、トウモロコシとネギを選びます。

問２

→合否を分けた一題参照。

問３

ここから一転して、ジャガイモとサツマイモに関する問題となります。
ジャガイモは茎、サツマイモは根に養分をたくわえたものであることは、知っての通りです。

問４

主な植物については、何科であるかをしっかりおさえておくことが大切です。
（１）ジャガイモはナス科の植物です。ナス科にはほかに、トマト、ピーマン、ナス、ホオズキなどがあります。
（２）サツマイモはヒルガオ科の植物です。ヒルガオ科にはほかに、ヒルガオ、アサガオなどがあります。

問５

光合成で得られた養分はデンプンです。「イモ」は、養分をデンプンのかたちでたくわえているので、ヨウ素デンプン反応で確かめることができます。

問６

「成長の仕方をふまえて」とありますが、リード文からは、植え方が異なる理由が具体的にはわかりません。このようなときは、これまでの問題の流れにそって考えるようにします。ジャガイモは茎、サツマイモは根であることを手がかりにすれば良いでしょう。たとえば、ジャガイモの茎は、種イモから発芽して上へ成長します。つまり、イモのできる地下茎は種イモよりも上から出るので、成長していくにしたがって、さらに土を被せて盛っていくと良いと考えられます。また、サツマイモは根なので、あらかじめ土を盛っておけば、その土の中につぎつぎと根を下ろして増えます。

４

（地学）堆積物の粒子の観察についての問題です。
リード文と写真から考えを進め、問いに答える問題です。決まった答えがあるとは言えないものもあり、手がかりを見落とさないように注意しながら、求められている答えを探っていく感覚が必要です。一筋縄ではいかない難問と言えます。

問１

表１から、堆積物Ａ〜Cには、顕微鏡で見ると、角張っているものや丸みをおびているもの、透明なものから黒いもの、繊維状のものや細長くうすいものなどがあります。問題では、顕微鏡を使用しない方法をきいているので、見た目ではない観点で物質を調べる方法を考えます。たとえば、密度に着目した場合、水に入れてよくかき混ぜてみると、沈む粒子と沈まない粒子があるかどうかを調べることができます。

問２

地層を構成していた物質のうち、流れる水のはたらきを受けて海水で堆積したものは、粒子の形が丸みをおびているはずです。堆積物Ａの粒子は、「角張っている」とあるので、少なくとも流れる水のはたらき（特に侵食作用）を受けていないという点で判断します。

問３

鉄は無色透明ではりません。ダイヤモンドは、「地球内部に豊富にふくまれている」はずはないので、不適当です。食塩は水に溶けやすい物質なので、堆積物にはなりません。したがって、石英を選びます。

問４

堆積物を採取した場所は３箇所で、表１と図２〜４から、堆積物Bは、堆積物ＡとCの特徴を併せ持っていることがわかります。正門前は屋外、教室内は屋内です。通路は屋外でありながら、教室内のように、おそらくは生徒の生活に関係したチリやホコリが混じる可能性があります。したがって、堆積物Bが屋外の通路、堆積物Cが教室内と判断できます。

問５

まず＜粒子の大きさと数を測定するときのルール＞を読みとかなければなりません。中でも「見えている範囲で最も長い対角線」の意味がわかりにくかったのではないでしょうか。残り時間によっては、すでに解いた問題の見直しに時間を当てた方が良いかもしれません。
（１）図６の測定の例に、ルールを当てはめてみます。粒子を大きさによって４つに分類していて、補助線の間隔より小、間隔１つ分から２つ分の間、間隔２つ分から３つ分の間、間隔３つ分より大きい、の順で大きくなります。「対角線」が最も長い直径をさしているとすると、図６の３つの粒子のうちでは、大きさが間隔１つ分の粒子が２つ、間隔１つ分から２つ分の間の粒子が１つあります。ルール⑤で、すべての交点について粒子の大きさを数えるとあるので、交点の場所にある小さい粒子１つについて、「〜1/4mm」に粒子数１を数え、交点２つをカバーしている大きい粒子については、「1/4mm〜1/2mm」に２つとカウントしなければならないことになります。
図５には、多くの粒子がありますが、測定するのは、補助線の交点が粒子に入っているものだけです。選択肢の粒子の分布のグラフは、粒子の大きさごとに、カウントされる粒子の数の割合を表しているので、まずはただ一つ3/4mmをこえている、右上の最も大きな粒子に着目すると良いでしょう。下の図のように、粒子の内側になる交点（●＋○）が全部で32個なのに対して、最も大きな粒子にかかる交点（●）は６個なので、（6/32）×100＝18.75（％）で、イかクにしぼられます。次に、「1/2〜3/4mm」の大きさのものを数えると５個なので、クが最も適当とわかります。
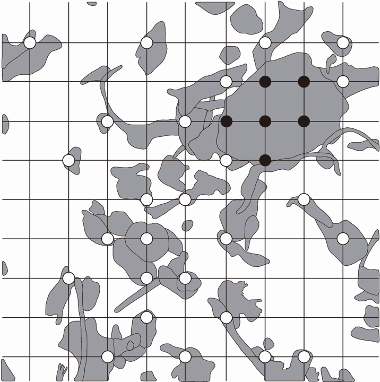
2020_gouhi_rika_01

（２）これまでの処理でわかるように、一つの粒子が複数の交点にかかる場合、交点の数をカウントすることになり、大きな粒子ほど実際より多く数えることになります。また、小さな粒子は交点にかからないものもあり、実際より少なく数えることになります。これを解決するには、まず、粒子数を交点ごとに数えるのではなく、粒子ごとに数えること。また、交点にかからない小さな粒子をひろうため、補助線の位置をずらして何通りか数えて、平均をとる方法などが考えられます。

合否を分けた一題

リード文と図、問題文のいくつかに分けて示されている条件を見落とさず、しっかりした知識と照らしながら、整理して考えることができたかどうかで合否が分けたと考え、この問題を取り上げました。

３

問２

どの選択肢も、リード文にある各野菜を植えたポットの数と、同じ種類はとなり合うように並べるという条件はクリアできています。次にチェックが必要なのは、図２から、子葉の数が１本の単子葉類の位置が正しいかどうかです。これで、ア〜エにしぼられます。さらに、☆のすぐ下のポットの子葉が卵型で、他の双子葉類より大きかったあることから、ここにキュウリがくることがわかります。最後に、☆の下３番目の子葉は細長い筒状であったことから、ここにネギを当てはめます。
細かい知識がなければ突き詰めることができない、少々難易度が高い問題と言えます。

著者：S.O.

この記事は役にたちましたか？