算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

城北中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1) A　　(2) A
［２］	(1) A　　(2) A　　(3) A　　(4) A　　(5）B　（6）C
［３］	①～⑥ A ⑦～⑩ B
［４］	(1) A　　(2) B 　　(3) B
［５］	(1) A　　(2) A　　 (3) B

Ａ：城北中学合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度・処理量から判断して、得点差がつかない問題

出題総評

今年の入試は大問５題、小問１７題という構成でした。速さではダイヤグラムの読み取りの問題、立体図形では切断の問題の出題でしたが、いずれも冷静の対処できれば正解できる問題だったのではないでしょうか。しかし、大問４の速さの問題などで、（１）を間違えると当然その答えは（２）以降でも影響がでるので、計算で必要以上に時間を費やしたり、正解までたどり着けなかったりした受験生もいたのではないでしょうか。算数の合格者平均点は７７点と高得点です。いかにミスを少なく抑えることができたかが合否を分けたカギとなったでしょう。

問題別寸評

【１】

計算点
（１）四則計算　（２）逆算

【２】

小問集合
受験生おなじみの２種類の食塩水を混ぜる問題です。
面積図や天秤をつかって３％食塩水と６％食塩水の重さの比が３：１であることがわかるので、
５４０ ×　 2018_gouhi_sansu 　＝３６０ｇ・・・・・３％食塩水の重さ
５４０ ×　 2018_gouhi_sansu_2 　＝１８０ｇ・・・・・6％食塩水の重さ
全体の仕事量を１４分と１０分の最小公倍数の７０とすると、１分当たりの注水量はＡ管で５、Ａ　管とＢ管の合計では７となるので、Ｂ管だけの１分当たりの注水量は２になります。よって７０の全体の水の量をＢ管だけで注水すると７０÷２＝３５分

正六角形を６等分すると1辺２０㎝の正三角形６個に分けることができます。一辺が３０㎝の正三角形と一辺が２０㎝の正三角形の面積比は３×３：２×２　＝９：　４となります。
よって９　：　４×６　＝３　：　８になります。

（４）おうぎ形の折り返しの問題です。ＯＡ＝ＡＤ＝Ｏであることに着目すると
三角形ＯＡＤは正三角形になるので、角ＡＯＤ＝60度であるとわかります。したがって、角ＢＯＤは　110度－60度＝５０度になります。三角形ＢＯＤは、ＯＢ＝ＯＤなので二等辺三角形ですから求めるアの角度は（１８０－５０）÷２＝６５度になります。

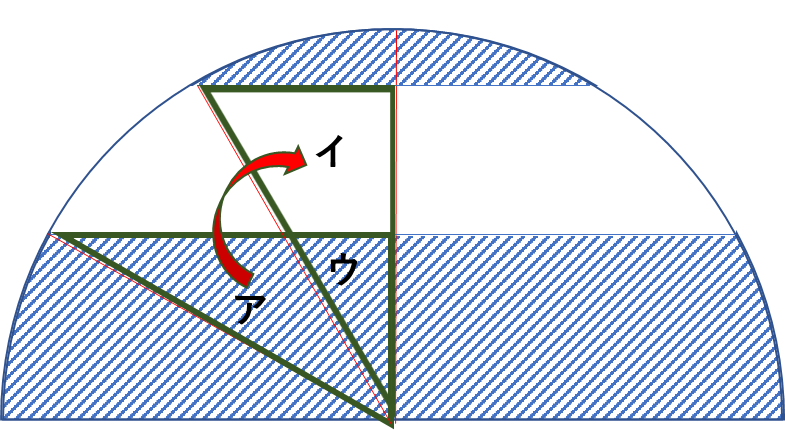
下図のように、ア＋ウの直角三角形と、イ＋ウの直角三角形が合同であることに気づけばアの部分の面積とイの部分の面積が等しくなります。アの部分を移動させると、中心の角度が３０度分のおうぎ形が４つ分になるので、
６×６×３．１４× 2018_gouhi_sansu_4 ×４＝３７．６８㎠
2018_gouhi_sansu_3

周期の問題です。６と５０の最小公倍数は１５０ですから、６個進んで白を黒に塗っていくと
１５０÷６＝２５周期繰り返し、２６周期目で１番初めに塗った黒石を2回目黒く塗ることになります。よって25個の白い石が黒く塗られたことになります。
　　　

【３】

Ａ＜Ｂ＜Ｃ＜Ｄのとき、　４つの数のうち２つの数の和の大きさはの関係は
Ａ＋Ｂ＜Ａ＋Ｃ＜Ａ＋Ｄ，Ｂ＋Ｃ＜Ｂ＋Ｄ＜Ｃ＋Ｄ　になります。
和の組みＡ＋Ｂ合わせが６種類あるのに和の値の種類が５種類しかありません。このときＡ＋Ｄ，Ｂ＋Ｃ　の大きさは同じであるといえます。
したがって、Ａ＋Ｂ＝１１，Ａ＋Ｃ＝１３，Ａ＋Ｄ＝Ｂ＋Ｃ＝１６，　Ｂ＋Ｄ＝１９，Ｃ＋Ｄ＝２１となります。ここで、ＢとＣの差に着目してみます。Ａ＋Ｂ＝１１，Ａ＋Ｃ＝１３であるので　Ｃ－Ｂ＝２であることがわかります。また、ＢとＣの和はＣ＋Ｂ＝１６だから和差算で（１６＋２）÷２＝９となり、Ｃ＝９，Ｂ＝７になります。よって　Ａ＝４　Ｂ＝７　Ｃ＝９　Ｄ＝１２

【４】

合否を分けた一題で解説します。

【５】

立体図形の切断の問題です。
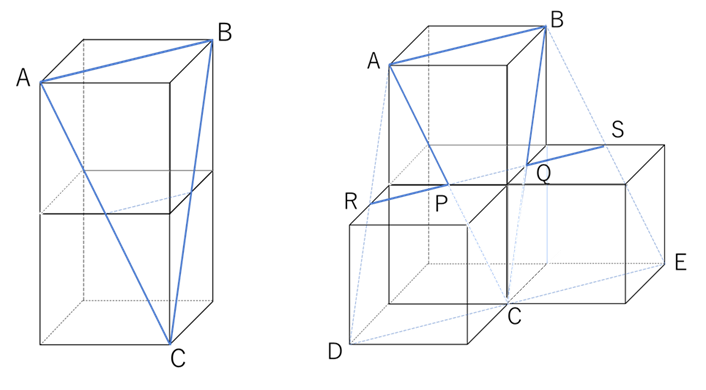
2018_gouhi_sansu_5

図１の三角形ABCが切り口になります。

三角形PQCと三角形ABCは、相似比１：２の相似形ですから、面積比は 1 ：　４となります。したがって台形ABQPの面積と三角形PQCの面積比は　３： 1とわかります。台形ABQP
　
切断した切り口は、図２のようになります。三角形PQCの面積が６㎠ですから、の面積は　６×３＝１８㎠です。切り口の面積は、台形ABQPが3つ分と三角形PQCを合わせたものであるから、１８×３＋６＝６０
６０㎠

合否を分けた一題

日ごろからダイヤグラムに慣れておかないと、緊張しながらの入試本番ではなかなかやっかいな問題です。今回はその中でも流水算からの出題でした。Pの上りの速さと下りの速さにいち早く着目し、（１）を落ち着いて解答できれば全問正解も可能です。ただし、（１）の答えが出ないと全滅という問題の作りになっているため、合否を分けた一題になったのではないでしょうか。

【４】速さ　ダイヤグラムの利用

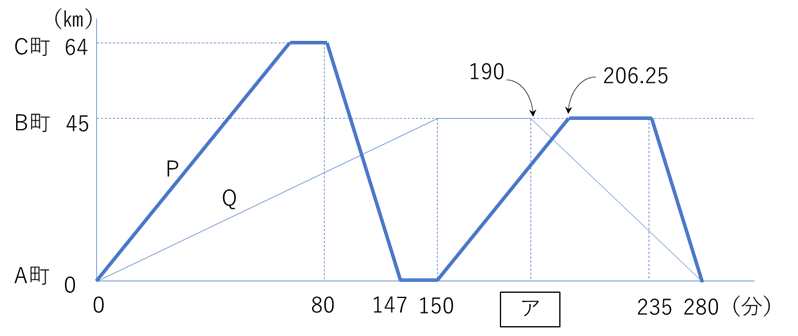
2018_gouhi_sansu_6

　６４÷ 2018_gouhi_sansu_7 ＝時速４８km　・・・・・　Pの上りの速さ
４５÷ 2018_gouhi_sansu_8 ＝時速６０km　　・・・・・　Pの下りの速さ

よってPの静水時での速さは（４８＋６０）÷２＝時速５４km

（２）（１）より　川の流れの速さは時速６㎞とわかります。
Qの上りの速さは、４５÷２．５＝時速１８㎞ですから、
Qの静水時の速さは時速２４㎞となります。
したがって、Qの下りの速さは時速３０㎞なので、QがAB間を下るのに必要な時間は、
４５÷３０＝１．５（時間）アの値は、２８０分から１．５時間前だから　ア＝１９０

（３）上のダイヤグラムの中の相似を利用して解くと、簡単に解答できます。
相似比は（２０６．２５－１９０）：（２８０－１５０）＝１６．２５　：　１３０　＝　１：８　
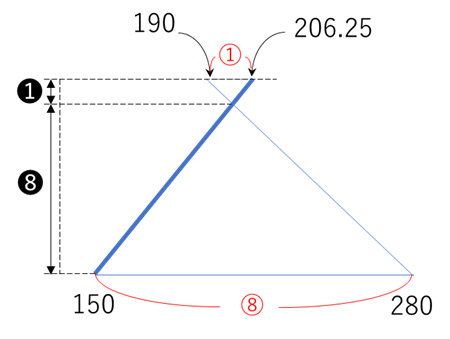
2018_gouhi_sansu_9
よって、２回目に出会った地点は、A地点から
４５ ×　 2018_gouhi_sansu_10 　＝　４０㎞　とわかります。