算数の合否を分けた一題
城北中入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| 1 | (1) A (2) A |
|---|---|
| 2 | (1) A (2) B (3) A (4) B (5) B (6) C |
| 3 | (1) A (2) B (3) B |
| 4 | (1) A (2) B (3) C |
| 5 | B |
A…城北中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、部分点を拾えればよしとする問題
出題総評
合格者平均は70点/100点満点、受験者平均は52点と、ここ3年ではやや点数が低め。問題ごとの難易差は比較的小さく、標準レベルの問題が並んでいます。空間図形は、切断、求積がやや難しく、ここも意識的に練習しておきたいところです。
問題別寸評
(1) (2)
基本的な計算問題です。
(1)
紙の折り返しと角度。時間はかからないでしょう。
(2)
立方体内部に接する正八面体の体積。上から見た底面積が立方体の1/2、すい体で1/3ですから体積は立方体の1/6になります。
(3)
食塩水の混合。標準的な問題です。
(4)
大 ÷ 小 =18あまり21ですから、
大 = 小 × 18 + 21 …①
もう一つの条件は
大 - 小 = 412 …② ですね。
②をよく見て、
小 × 17 + 21 = 412
ここから小、大の数を求めていきます。
(5)
売買損益。定価=1.3、2割引き=1.04、5割引き=0.65のそれぞれに個数の比をかけて全体の個数を表す数字で割ります。
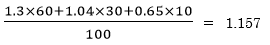 …これが総売り上げですから、利益の0.157が94200円ということですね。円周率関連の数字が並んでいますが、関係ありません。
…これが総売り上げですから、利益の0.157が94200円ということですね。円周率関連の数字が並んでいますが、関係ありません。
(6)
平面図形の面積。星の形が出てきますが、アンバランスのため、見た目同様にすっきりとは求められない問題です。点Dと点Gの突起を白いところに移すなどの工夫をしてみましょう。時間がかかった受験生が多かったのではないでしょうか。
後述します。
(1)
台形の面積を求める誘導問題です。
(2)
上から見た平面図をかいて、その平面上で考えましょう。標準レベル。
(3)
切り口が斬新な力作です。見えそうで見えない、把握しづらい立体だったと思われます。
しかもいわゆる「断頭三角柱(三角柱の切断体)」です。(1)の誘導に乗るなら、三角形RBQで切って2つの部分に分けて求積、という方針に落ち着くというところでしょう。
「断頭三角柱」の公式: 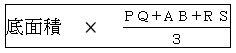 は知っていると有利でしょうね。
は知っていると有利でしょうね。
誰もが1度はやったことがあるタイプの問題。正方形の面積による分類および個数を表にまとめ、空欄を埋める形式で答えます。まっすぐな向きの正方形はそのまま数え、「斜め」の正方形は、外枠のまっすぐな正方形の個数と斜めの向きを考えて個数を出していきます。
できることなら、やみくもにスタートせず、たとえば
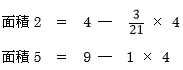
といった具合に、外枠の正方形から4つの直角三角形を取り除く、という方針で数えていけば、漏れも減り、スピードアップも図れるでしょう。
たとえ未知のものであっても、行き当たりばったりの勝負に出ない習慣を日ごろから養っておきたいところです。
合否を分けた一題
大問3の速さを取り上げます。難度としては標準レベルですが、問題を見てすぐに全体像が見える受験生と、そうでない受験生とで、処理スピードで差がついた可能性があります。
(1)
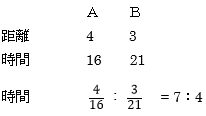
と即決できればOK。
(2)
CはABを4:3に分ける点で
DはABを2人の速さ比7:4に分ける点ですから、
2種類の比(連比)をそろえる方針を立てると、
AC:CD:DB=44:5:28にたどり着くでしょう。図形分野ではおなじみの処理ですね。
(3)
44の距離に16分
49の距離に 分 と考えて求めましょう。
比の表がすぐに書けるか、連比の処理にすぐ入れるか…日ごろの練習の成果が出やすく、勉強量が結果に反映しやすい問題ということができるでしょう。標準レベルの問題をやりこんで、速さと正確さを磨きましょう。
城北中入試対策・関連記事一覧
城北中入試対策・同じ教科(算数)の記事
城北中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2015年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)