算数の合否を分けた一題（2015年度）

算数の合否を分けた一題

城北中入試対策・算数の合否を分けた一題（2015年度）

難易度分類

［１］	（１）Ａ　（２）B
［２］	（１）B　（２）A　（３）A　（４）B　（５）B　（６）B
［３］	（１）Ａ　（２）B　（３）B
［４］	（１）Ａ　（２）Ｂ　（３）A
［５］	（１）Ｂ　（２）（ア）C　（イ）C

Ａ：城北中合格を目指すなら必ず得点したい問題
Ｂ：知識・着眼点・解法により正答率やかかる時間に差がつく問題
Ｃ:難易度、処理量から判断して、一旦保留にしてもよい問題

問題別寸評

［１］計算問題

（１）少数、分数の変換に注意。
（２）１．２３でまとめる事。そのまま左から普通に計算してしまうとえらい時間がかかってしまいます。２．４６も３．３９も１．２３の□倍になっていることにパッとみて気付けるようにしておこう。

［２］小問集合

（１）仕事算と比
全体の比をA:B=11：１３としてつるかめ算を利用しましょう。Aは１１を１ずつ排出していくので、その時にかかる時間は11÷１＝⑪分とおく。Bも同じ時間で終了したので⑪分とすると、はじめは１ずつ、あとから２ずつ排出していき、合計⑬の量を終了するというつるかめ算を利用しましょう。

（２）平面図形
平行四辺形の対角は同じ角度なので、角ABCをもとめるようにしましょう。

（３）半径と角度を間違わないようにしましょう。

（４）ある数を□とすると、小数点を左に一つずらした数は□×０．１となります。
□—□×０．１＝１８．１３５
この式を解きましょう。

（５）ダブりと０を含むカードの並べ方
百の位を１と2の場合で樹形図を書きましょう。

（６）サピックスの生徒はよく見かける問題ですね。
加比の理を使います。

［３］図形の移動とグラフ

（１）長方形Aと長方形Bの出会い算です。

（２）長方形Aが4秒後から１２秒後までに動いた線を描きましょう。
そうすれば、Aの速さから横の長さを求める事が出来ます。

（３）アが求められれば簡単です。イは、長方形Aが長方形Bに接してから完全に入るまでの時間ですよね。

［４］立体

（１）相似形を見つけましょう。

（２）どこに三角すいEFHJが出来るか。またその高さはどこになるのか。それを見つけられれば簡単です。

（３）普通にそれぞれ体積を求めても良いですが、比を利用して解いてみましょう。
Aから垂直にのばした点をOとすると、O-EFHの三角すいーO-AIJを引くという考えたより、
体積比を求めると、O-EFH：O-AIJ＝２７：８。
求める体積の部分は２７−８＝１９
８＝4×4÷２×１２÷３＝３２
１＝３２÷８＝４なので、１９＝４×１９＝７６㎠

［５］数の性質

（１）上の表より、新たに加える点は4個

（２）（ア）
同じ点になるところはどんどん消していく。はと同じ。つまり約分出来るものは、同じ分数になります。そういうものを全部消していくと、
１＋２＋２＋4＋２＋６＋4＋６＋４＝３１個

（イ）
一番距離が短くなるのは、との間になります。ー＝

合否を分けた一題

［３］の図形の移動

AもBも動くということと、グラフをしっかり読み取るということがこの問題のポイントです。
（１）グラフより、4秒間で長方形Aと長方形Bが出会ったということに気付きましょう。
はじめ１８㎝離れているので、１８÷４＝４．５←これはAとBの速さの和
なので、４．５−２＝２．５が長方形Aの速さとなります。

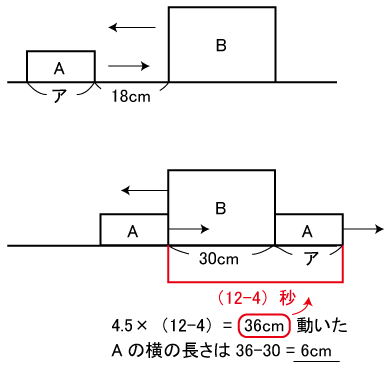
（２）長方形Aの横の長さですが、図形から読み解くことは情報が少ないので無理です。
ということは、やはりグラフか速さから求めるしかないでしょう。で、グラフを見ると、4秒と１２秒の部分が出ています。この２つの情報から何が解るのか考えてみて下さい。グラフの縦軸は面積、つまり長方形Aと長方形Bが出会ってから、出会い終わるまでの重なっている面積を表しています。図で表すと、以下です。