算数の合否を分けた一題
女子学院中入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| [1] | (1)A (2)B (3)㋐A ㋑A ㋒A (4)A (5)B …解答箇所5つトータルで (6)B |
|---|---|
| [2] | A |
| [3] | A・B |
| [4] | (1)A (2)①A ②A |
| [5] | B |
| [6] | (1)A・A (2)A (3)B (4)B |
A:JG合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、飛ばすことも考慮すべき問題
問題別寸評
1枚目は例年通りの小問集合です。
(1)計算問題
順算の計算問題。
特に工夫が必要というわけでもなく、いたって普通の計算問題です。
(2)計算問題
2か所の□には同じ数が入るという計算問題。
このタイプの計算問題は、□にあてはまる同じ数を①とおいて、マルイチ算の式処理に持ち込む解法が無難でしょう。左辺を計算すると 20/17 です。左辺と右辺の分子・分母でたすきがけをすると
20(①-33)=17×① となり、①=220と求められます。
(3)角度
JG頻出の角度問題で、正方形とおうぎ形の組み合わせ図形。「二等辺三角形の利用」という定石を確認するような出題です。JGの角度としては非常に易しく、合格のためには解答箇所3つとも正解が必須です。
(4)売買損益
原価を①とおいて、A店とB店それぞれの売値を求めて比較するだけです。
(5)和差比
JG頻出の解答箇所が多い問題。図1の「最後の黒い石」が、黒を2個並べるうちの1個目の場合と2個目の場合で答えが2通り出てきます。その点が把握できれば易しい問題です。
ただし、このような解答箇所が多い問題の怖さは、冒頭を誤答してしまうと、そのあとも連鎖的に誤答になってしまう点です。留意しましょう。
(6)平面図形と比
1枚目の最終問題です。辺の長さの比がわかっている方の長方形は処理できても、辺の長さの比がわかっていない方の長方形の処理で手が止まった受験生が少なからずいた様子。1本の補助線で突破口が開けます。ADを結び、長方形の半分にあたる三角形を作り出すことができたかがカギです。
➡ 合否を分けた一題
数の性質~最大公約数
ここから問題用紙2枚目です。
2数の最大公約数と和から、該当する2数を求める問題。これまで何度も解いたことがある問題でしょう。互いに素という条件をうっかり忘れずに。
ニュートン算
解答箇所1個目は普通のニュートン算、解答箇所2個目がニュートン算とつるかめ算の融合問題。はじめにあったケーキの数、1人が1分で箱に詰めるケーキの数、どちらを設定しても構いません。普段とっているニュートン算の解法で正答が出せればOKです。
立体図形
(1)
円柱の側面積を求めるだけです。
(2)
①おなじみの正十二角形の面積。30度・60度・90度の直角三角形の利用は、受験生には必須の知識です。
(2)
②円柱の容器に入れた水を正十二角柱の容器に入れ替えたときの深さを求める問題。水量をまともに計算することなく、分数式で処理しましょう。
調べ
ここから問題用紙3枚目です。
立方体の展開図において、向かい合う面の、①和が3組とも異なる、②和は7にはならない、という2つの条件を満たすように、1から6までの整数を面に書き込む問題。6の位置が固定されており、その向かい合う面に入る可能性がある整数をすべて答えるのですが、条件②より「1」はカット、残りの「2」「3」「4」「5」の4つの場合を調べればもれなく調べたことになります。もれなく調べる方針が立った調べの問題は、残り時間との勝負。時間がかかると予想してとばすか、時間に圧迫されつつ調べ上げるか。この問題程度の処理量であれば、後者を選択すべきでしょう。
速さと比+ダイヤグラム
(1)
与えられた問題文をもとに、①~④の中から正しいダイヤグラムを選ぶ問題。兄の休みは1往復するごとなので、②・④は×。兄と妹が同じ位置から出発か、向かい合わせで出発かは問題文には書かれていませんが、兄が妹より速く、20mプールを妹が16m泳いだときに初めて兄とすれちがったことを考えると、同じ位置から出発したことになるので③も×。自動的に①が答えになります。
(2)
実際の時間は兄の休む時間しか与えられていないので、そこを利用するしかありません。兄が5往復するのにかかる時間と妹が4往復するのにかかる時間が等しいことから、距離比÷速さ比=時間比を求め、その差が兄の休んだ40秒間となることに気づくかどうかです。
(3)
設問(1)で選んだ①のダイヤグラムを利用します。ダイヤグラムの中にあるクロス型相似をとらえるのが最短距離の解法でしょう。昨年度も大問[6](2)は、ダイヤグラムをかいて相似を利用する解法が有効な問題でした。次年度以降もおさえておきたいところです。
(4)
(4)も(3)と同様に①のダイヤグラムを利用しましょう。途中までしかかかれていないので、その続きをかき加えていけば、(3)とまったく同じクロス型相似が登場します。
合否を分けた一題
2021年度は、昨年2020年度と比べて大幅に難度を下げました。直近10年間で最も易しい2017年度に次ぐ易しさでしょう。解答箇所が24か所と、例年に比べて少ないことも、解きやすさの一因です。
受験生の間で差がつく可能性があるのは、連鎖的誤答が怖い[1](5)、補助線で勝負が決まる[1](6)、もれなく調べ上げる手法をとったかどうかの[5]、正しいダイヤグラムを選び、それを利用して解き進めたかどうかの[6](4)です。
このうち、問題用紙1枚目という早い段階で足止めをくらい、どこまで時間をかけたかで残り時間に影響を及ぼした可能性がある[1](6)を今年度の合否を分けた一題として取り上げます。
(6)
2つの長方形を重ねてできた図形(太線で囲まれた図形)の面積を求める問題です。
2つの長方形のうち、まずは「辺の長さの比がわかっている方の長方形」(長方形㋐とします)に注目しましょう。
AB:BC=11:4とCD:DE=1:3より、AB=11cm、BC=4cm、CD=1cm、DE=3cmとします。
内部にある2つの直角三角形と長方形㋐の面積はそれぞれ
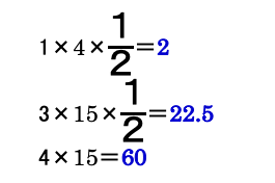
2つの長方形が重なった部分の面積が14.2㎠より
60-(2+22.5)=35.5
35.5=14.2㎠
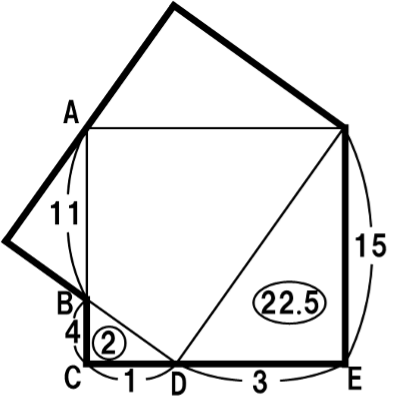
次に、「辺の長さの比がわかっていない方の長方形」(長方形㋑とします)に注目しましょう。
ADを結ぶ補助線を引きます。
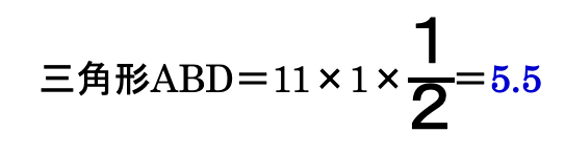
35.5-5.5=30
この面積30の三角形が、長方形㋑の半分にあたることに気づいたでしょうか。

長方形㋑=30×2=60 より
太線で囲まれた図形=60+2+22.5=84.5
35.5=14.2㎠ より
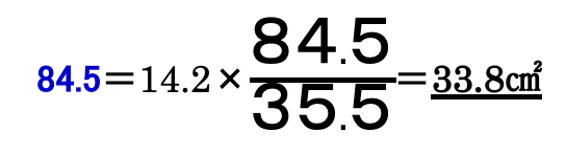
女子学院中入試対策・関連記事一覧
女子学院中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 算数担当講師から女子学院中学入学を目指す受験生へのアドバイス
- 時期による算数の学習法の提案(6年生)前半
- 時期による算数の学習法の提案(6年生)夏休み
- 時期による算数の学習法の提案(6年生)後半
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
女子学院中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)