算数の合否を分けた一題
女子学院中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| [1] | (1)A (2)A (3)A (4)A (5)A (6)A |
|---|---|
| [2] | (1)A~B (2)B |
| [3] | (1)A (2)A (3)A |
| [4] | ア A~B イ B~C ウ A~B |
| [5] | (1)A~B (2)B (3)B |
| [6] | (1)B (2)B・B・B |
A:JG合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、飛ばすことも考慮すべき問題
問題別寸評
例年通り、1枚目全体を使って小問集合の形で出題されました。
JGの大問1としては、難度はやや控えめでした。
(1)計算問題

(2)平面図形(面積)
例えば点Aから辺BCに垂線を下ろすと、「30度・60度の直角三角形」(根本原理ポイント 基礎編047)が現れます。下ろした垂線の長さは9cmの半分で4.5cmと分かるので、ひし形ですが平行四辺形として、底辺×高さで面積を求めることが出来ます。
JG合格レベルの受験生には基本的な出題でした。
(3)平面図形(角度)
図のように、2本の曲線の交点をEとし、AEとBEを結びます。

図で青く示した三角形は3辺とも円の半径なので正三角形です。
このことから三角形AEDはAD=AEで角A=30°、角D=角E=75°の二等辺三角形であることが分かります。角㋐は角Dの錯角になっているので、75°です。
この後、三角形BCFに注目すると、BC=BFの二等辺三角形になっていて、角FCB=180-(53+75)=52°です。よって、角FBC=180-52×2=76°であり、角㋑=90-76=14°と分かりました。
JG受験生は何度も練習している形であり、多くの受験生が正三角形をつくる補助線を発見できたはずです。
(4)割合と比(マルイチ算)
ジャガイモ1個の値段を10(または1)と置くのが分かりやすいでしょう。
ジャガイモ1袋は、10×4×0.9=36、にんじん1本は36÷3=12と表せます。
よって、10×2+36×1+12×5=116が754円に相当し、ジャガイモ1個の値段は、754÷116×10=65円です。
(5)規則性・日暦算
「1日おき」とは「○×○×○×……」、すなわち活動した「2日後」に次の活動を行うということです。
同様に「2日おき」は「3日後」、「3日おき」は「4日後」と言いかえられます。
さらに土曜日は7日ごとにやってくるので、2日、3日、4日、7日の最小公倍数である84日後に、3人が土曜日に一緒に活動することになります。
(6)平面図形(角度)
大問1の最終問題ですが、本年度は基本的な出題でした。
㋒→㋑→㋐→㋔→㋓の順に、注意深く○か×を付けていけば、ミスも起こりにくいでしょう。
(1)
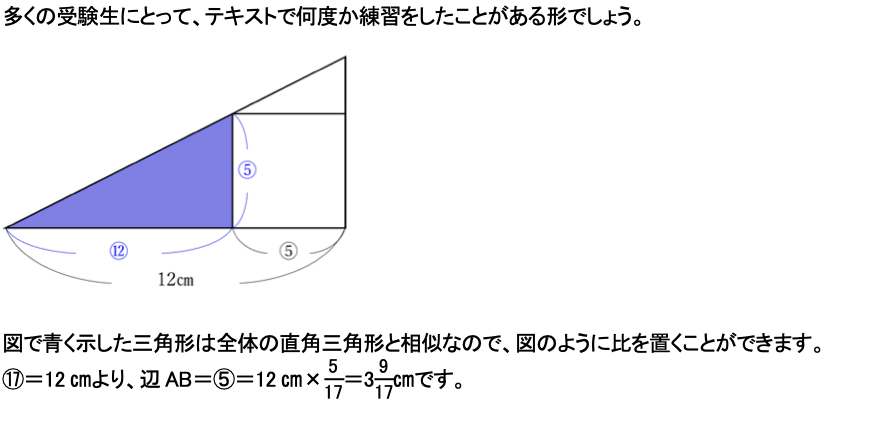
(2)

「新傾向」というよりも、算数の原点に立ち返ったような出題です。いずれにせよ、JGではあまり見られなかった形式と言えます。
全体に基本的な内容ではありますが、(2)では戸惑った受験生がいたかもしれません。
積が1であるような2つの数について、一方を他方の逆数といいますが、逆数とは分母と分子をひっくり返してできる数のこと、という程度の認識だった受験生には、解答にたどり着きにくかったことでしょう。
題意が捉えにくく、試験場では苦しんだ受験生も多そうですが、問題の状況をつかめれば3つの解答箇所のうち、少なくとも2つは容易に答えが得られます。
合否を分けた一題として、後述します。
問題に与えられた規則にしたがって作業をする中で、規則をつかみながら解答していきましょう。
(1)
例えば、表の1行目に注目してみましょう。数が分かっているマス目はBの12だけです。この12に○をつけ、①の規則にしたがって同じ行と同じ列に並んだ数に×をつけると、下のようになります。
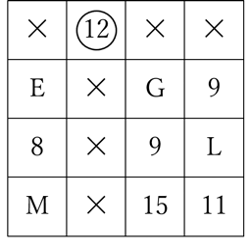
これによって、2行目で分かっている数がHの9だけになったので、そこに○をつけ、②の規則にしたがって×もつけると下のようになります。
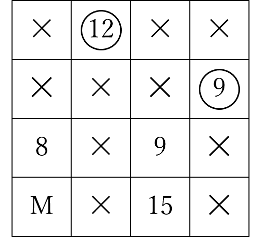
3行目にはまだ2つの数が残っていますが、4行目に残っているのは15だけになりました。③の規則にしたがってこれに○をつけ、その後×をつけて残った数に○をつけると下のようになります。
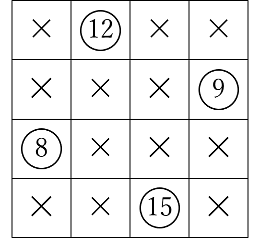
これで作業が完了しました。丸のついた数は4個で、これらの和は12+9+8+15=44です。
(2)
Aに入っている数を求めたいので、まずはAのマスに○をつけ、規則にしたがって×もつけると下のようになります。
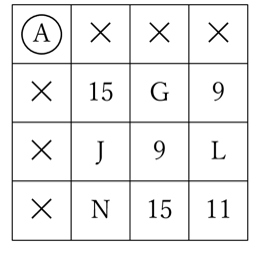
縦の2列目に注目するとFのマスの15のみが残っているのでここに○をつけ、規則にしたがって×もつけると下のようになります。
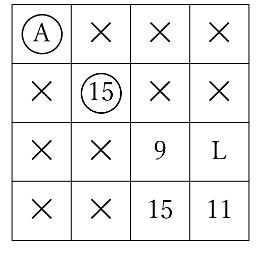
さらにKのマスの9に○をつけ、規則に従うと下のようになります。
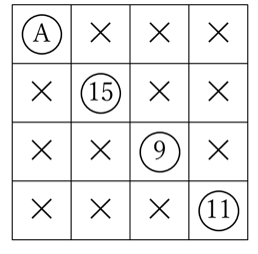
丸のついた4つの数の和は(1)で求めた44になっているはずなので、Aに入っている数は、44-(15+9+11)=9と分かりました。
Gに入っている数も、同様の作業で求めることができます。
(3)
(2)で行ったのと同様の作業を繰り返せば、すべてのマス目の数を求めることができます。
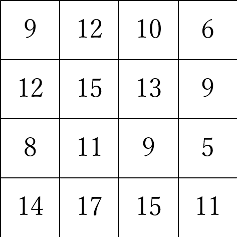
作業が完了すると上の表のようになり、一番大きい数は17、一番小さい数は5であると分かります。
作業の途中で、例えば1列目と2列目の数の差はどの行でも3になっているなど、列や行ごとに隣同士の数の差が等しくなっていることに気がつくと、処理時間が大きく短縮できるところでした。
最終の大問として易しすぎも難しすぎもせず、力の差がはっきり現れたと思われます。(1)において、流水上での出会いでは2人の静水時の速さの和で近づくことを利用できたかどうかが正否の分かれ目になりました。
(1)
以下のように、流水上での出会いでは2人の速さの和が静水時の速さの和に等しくなることに注目します。
姉の下りの速さ=姉の静水時の速さ+川の流れの速さ
姉の上りの速さ=姉の静水時の速さ-川の流れの速さ
妹の下りの速さ=妹の静水時の速さ+川の流れの速さ
妹の上りの速さ=妹の静水時の速さ-川の流れの速さ
のように表せることから、
姉の下りの速さ+妹の上りの速さ
=(姉の静水時の速さ+川の流れの速さ)+(妹の静水時の速さ-川の流れの速さ)
=姉の静水時の速さ+妹の静水時の速さ
と、川の流れの速さが打ち消され、2人の静水時の速さの和と等しくなっています。
同じように、姉の上りの速さ+妹の下りの速さも、2人の静水時の速さの和に等しいことが分かります。
姉が下って妹が上るときには、A地点から1.8km、すなわちB地点から0.6kmの地点で出会っているので、(姉の下りの速さ):(妹の上りの速さ)=3:1。
同様に、姉が上って妹が下るときには、A地点から1.5km、すなわちB地点から0.9kmの地点で出会っているので、(姉の上りの速さ):(妹の下りの速さ)=3:5。
ここで、いずれの出会いでも2人の速さの和が等しいことから、上の2つの比の和を統一することにより、
(姉の下りの速さ):(妹の上りの速さ):(姉の上りの速さ):(妹の下りの速さ)=⑥:②:③:⑤
であることが分かります。
姉の下りの速さ-姉の上りの速さ=③は、川の流れの速さ=15m/分の2倍にあたるので、③=30m/分より、①=10m/分です。
よって、姉の上り=30m/分、姉の下り=60m/分、妹の上り=20m/分、妹の下り=50m/分であり、これらから、それぞれの静水時の速さも得られます。
(2)
(1)で速さが求まっているので、2人が上り・下りにかかる時間を計算すると、
姉の上り…80分
姉の下り…40分
妹の上り…120分
妹の下り…48分
となります。
これらをもとに、2人の動きをダイヤグラムに表すのが良いでしょう。
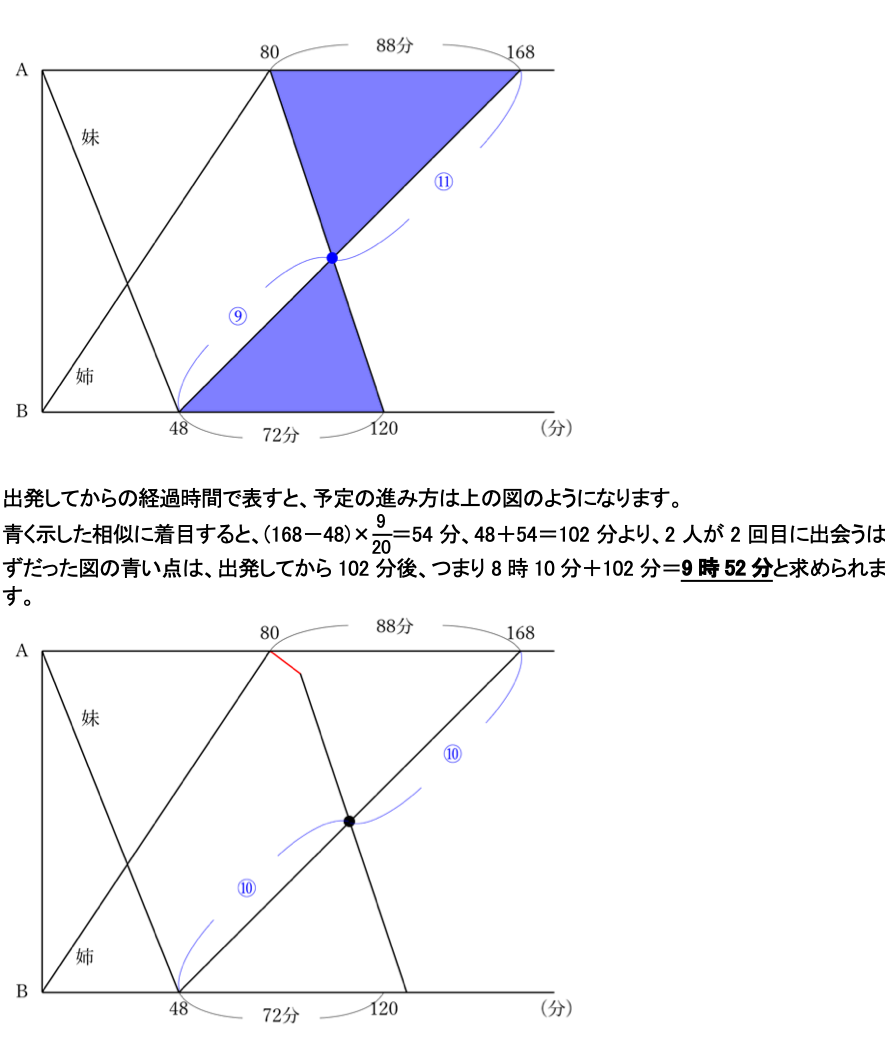
実際には、姉が図の赤い線の部分でボートをこがずに川の流れだけで進んだため、出会う位置がずれました。「A地点から1.2kmの地点」とは、ちょうどAB間の真ん中にあたります。
妹に注目すると、出会ったのは48分と168分の真ん中、すなわち出発してから108分後の9時58分であることが分かります。
3つの解答箇所のうち、2つ目が最後に残りました。
姉は、80分から108分までの28分間で、川の流れの速さである15m/分と下りの速さである60m/分を合わせて、1200m進んでいます。
ここまで整理できれば、あとはつるかめ算を用いて答えを求めることができます。
合否を分けた一題
昨年2019年度は、易しかった2017年度、2018年度と比べて大幅に難化した年でした。
本年2020年度は、昨年度の[6]のような難問はないものの、数値がやや煩雑だったり、題意が捉えにくかったり、手順が多かったりと、全体に適度な難易度に収めた上で、随所に差がつきそうな問題が散りばめられていました。
短い試験時間内での処理能力も問われ、入学試験として適切な実力差のつくセットであったと思われます。
さて、2020年度の合否を分けた一題としては[4]を取り上げます。
試験場では題意をつかむのにやや時間がかかった受験生も多そうですが、いざ問題の状況を理解してしまえば、3つの解答箇所のうちウ→アの順で2つは比較的簡単に答えを得られます。
点が移動する辺の長さは3種類。立体の高さが6cm、底面上の直線部分はすべて3cmで、曲線部分は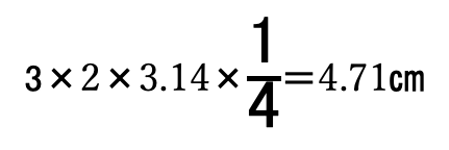 です。
です。
与えられた立体の図から、点Pは、
6cm→3cm→4.71cm→6cm→3cm→6cm→3cm→6cm→3cm
の順に、立体の辺を動くことが分かります。
ウは、このうち6cm→3cm→4.71cmと動いたときの道のりを表しているので、これらを加えて13.71cmです。
アは、点Pが最後まで動いたときの道のりですから、上の9つの数値をすべて加え、40.71cmです。
イについては、グラフの辺の途中にある点なので、もう少し状況を整理しなくてはなりません。
問題文中の「点Pが6cmの辺上を動くときの速さは、3cmの辺上を動くときの速さの2倍」という条件から、「6cmの辺上を動くのにかかる時間と3cmの辺上を動くのにかかる時間は等しくなっている」ことが分かります。これがこの問題の最大のポイントです。
グラフの9.21秒から16.71秒の部分では5本の辺を動いていますが、すべて3cmか6cmの辺なので、5本ともかかる時間は同じです。
(16.71-9.21)÷5=1.5より、3cmや6cmの辺を動くのにかかる時間は1.5秒であることが分かります。
イは14秒の時点で動いた道のりを表していますが、グラフからこのとき点Pは8と9の間にいることが分かります。
点Pが9にいるのは、16.71-1.5=15.21秒のときで、14秒の時点はこの1.21秒前です。
8~9において、点Pは6cmを1.5秒、すなわち秒速4cmで動いています。
よって、
40.71-3=37.71cm … 9までに点Pが進んだ道のり
37.71-4×1.21=32.87cm … イ
女子学院中を目指す受験生は、計算処理のスピードだけでなく、正確に問題文の意味をつかむ力も求められます。全体の問題を考えて、どの問題から取り組むべきかを素早く考える練習もしておきましょう。
女子学院中入試対策・関連記事一覧
女子学院中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 算数担当講師から女子学院中学入学を目指す受験生へのアドバイス
- 時期による算数の学習法の提案(6年生)前半
- 時期による算数の学習法の提案(6年生)夏休み
- 時期による算数の学習法の提案(6年生)後半
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2021年度)
女子学院中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)