算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

女子学院中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	（１）Ａ　（２）Ａ　（３）①Ａ～Ｂ　②Ａ～Ｂ　（４）㋐Ａ　㋑Ａ　㋒Ａ　（５）Ｂ
［２］	（１）Ｂ　（２）Ｂ
［３］	（１）Ｂ～Ｃ　（２）Ｂ
［４］	長針と短針がつくる角Ｂ　時刻Ｂ
［５］	菓子Ｂ　売り上げが最大になるときＢ
［６］	Ｃ

Ａ：ＪＧ合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、飛ばすことも考慮すべき問題

問題別寸評

［１］

例年通りの小問集合です。

（１）計算問題

JGの計算問題としては標準的です。
答えの分母に「2019」が現れますので、少しだけ安心感があるかもしれません。

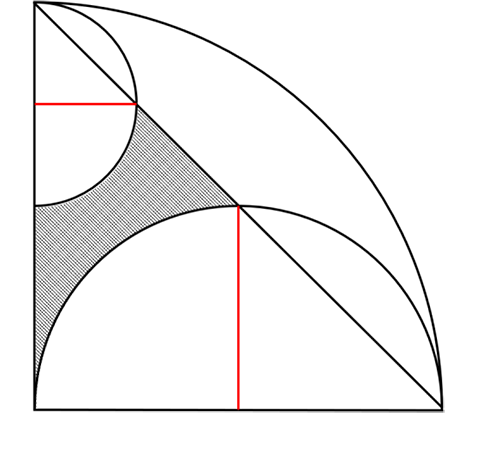
（２）平面図形・面積

おうぎ形に絡んだ求積の問題です。
図のように赤い補助線を入れることができれば、直角二等辺三角形やおうぎ形の面積の足し引きをして、答えを得ることは難しく,ありません。

（３）約束記号

分数式は、分子÷分母と書き換えられることを利用して求めます。
たとえば、①は、
1÷(1－[A])＝3
という式に書き換えることができます。
これより、1－[A]＝1/3 → [A]＝2/3 → A＝3/2と求められます。
②も、式の右下部分から丁寧に計算することで答えが得られます。
試験場では、ある程度の差がつく問題の1つであったと思われます。

（４）平面図形・角度

JG合格レベルの受験生にとって、ぜひ正解したい問題ではありますが、こちらも受験生間で差のついたことでしょう。
円やおうぎ形の折り返しでは、正三角形に注目することがポイントです。図で、弧ABの中点をPとすると、三角形OPEやOPFは正三角形です。したがって、角EOF＝120度。
また、四角形ABCDが正方形であることから角AOB＝90度であることに注目して、㋐を求めることができます。
一方、㋑と㋒は、㋐と無関係に求められます。

正方形ABCDは､対角線BDについて対称になっていますので、図で赤く示した角も㋑と等しくなっています。このことから、
㋑＝(180°－32°)÷2＝74°
と求められます。
㋑が求まれば、角DBC＝45°であることを用いて、㋒は容易に求められます。

（５）相当算

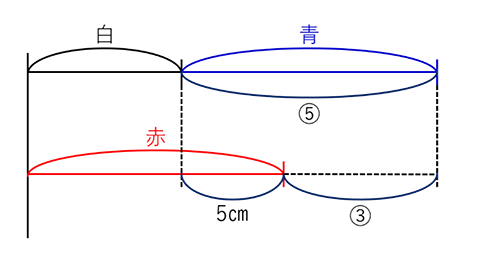
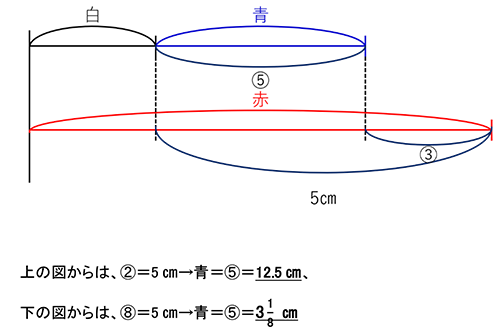
問題の状況を線分図に表すと、「青の上に白をのせたもの」が「赤」より高い場合と低い場合に対応して、以下の2通りの図が描けます。

と2つの答えが得られます。
線分図が描ければ容易ではあるのですが、問題文の「青の上に白をのせたもの」を「白の上に青をのせたもの」と読み替えると有効な線分図が描きやすくなるなど、処理速度に差が出る問題でした。

［２］平面図形・図形の移動(円の転がり)

（１）

小円が転がったときの中心の移動距離を問うという設定自体は、非常によく見られる出題ですが、細かいところで勘違いやミスを起こしやすく、自信を持って答えを得た受験生はあまり多くないかもしれません。
小円は、点Bのまわりでは90度、点Cのまわりでは60度転がることを確認した上で、分数の形で残った値を、指示通り小数第2位で四捨五入するところでも計算ミスに注意しなければなりません。

（２）

弧BCの長さは、4×2×3.14×1/3＝8/3×3.14 （㎝）、
円の周の長さは、1×2×3.14＝2×3.14 （㎝）です。
よって、8/3÷2＝4/3より、円がBCを転がる間に、円が太線と接している点は円周上を反時計回りに4/3回転移動した位置に変わります。
4/3回転とは1周と1/3回転、1周の分を無視すれば1/3回転と同じですから、Bで接していた点から円周上を反時計回りに120度移動した点がCに接するように描いた図が正解となります。
処理量としては今年のセットの中では少なめで、取っておきたいところですが、何らかのミスをした受験生も多かったでしょう。

［３］展開図・調べ上げ

（１）

立方体の展開図は回転や裏返して同じになるものを１つと数えると、全11種類。JG受験生であれば、すべて頭に入っているはずですが、だからと言って、この問題を短い時間の中でもれなく数え上げるのは容易ではありません。
試験での作戦としては、あまり時間をかけずにさっと答えを書いておいて、時間が残れば最後に再検討するという形が良さそうです。

（２）

こちらも、厳密に答えようと思えば、すべての展開図を書き上げて調べるしかありません。現実的には、和が小さくなりそうな展開図をいくつか検討し、その中から最も小さいものを解答として書いておくほかないでしょう。
ただ、なるべく下段の数字を使わないような展開図を考えることで、試験時間中に正解を得られる可能性は（1）よりもかえって高そうです。
いずれにせよ、試験本番では、あまり時間をかけすぎるべき設問ではありません。

［４］時計算

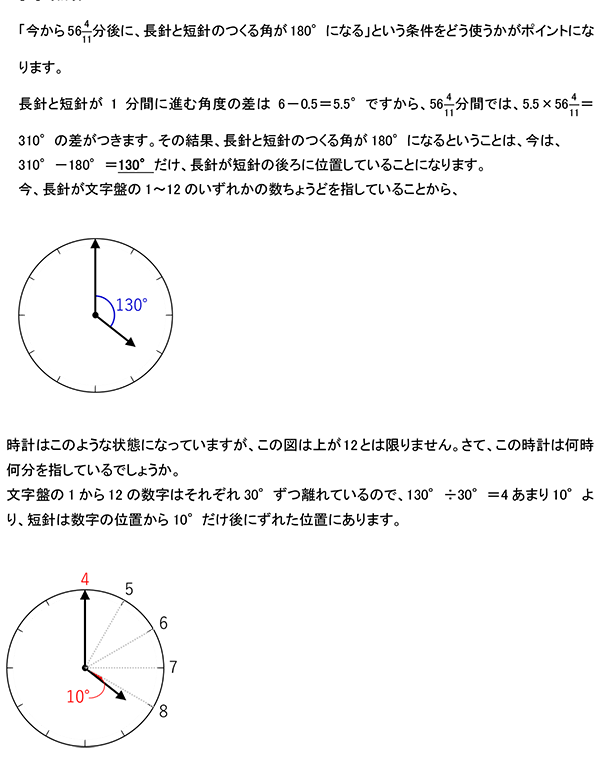
短針が数字ちょうどの位置から10°進むのには20分かかりますので、この時計が指している時刻の分は「20分」です。したがって、今、長針は4の位置にあります。
あとは、上図のように短針の位置まで数字を振れば、求める時刻は「8時20分」であることが分かりました。

類題を経験していたかどうかが、正否を分けそうな設問でした。

［５］数の性質・過不足算・不定方程式

無理のない難度ですが、合格者と不合格者の間で、正答率・処理速度ともに大きな差がついたのではないかと思われます。
合否を分けた一題として、後述します。

［６］集合算

一見よくある集合算のようにも見えますが、取り組んでみると条件の整理の仕方が難しく、試験時間中に正答に至るのは相当困難な出題でした。

4つの競技があるので、通常のベン図には表しにくく思えます。ここで、（ア）の「サッカーと卓球の両方に出場する生徒はいません。」という条件から、

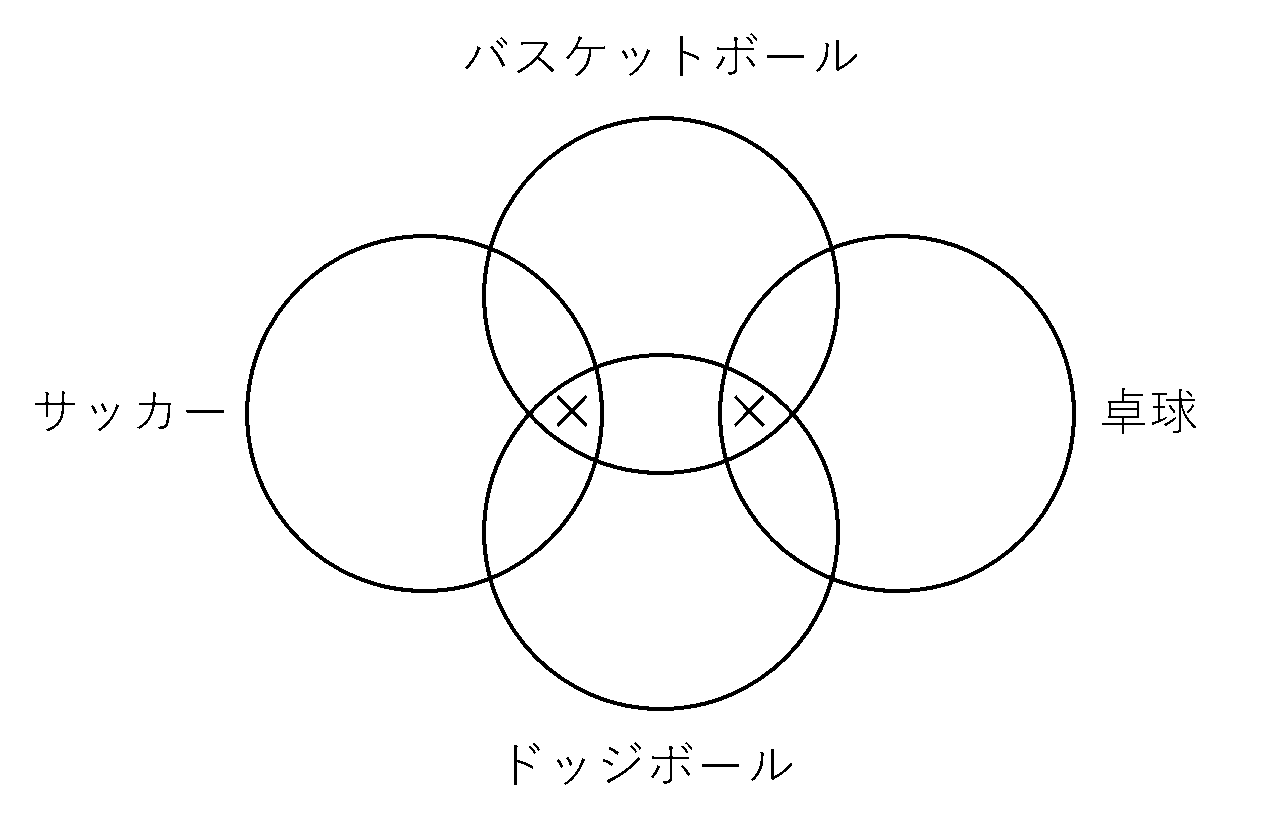
サッカーと卓球を表す円同士は交わらないように書いても問題が無いので、上のような形のベン図に問題の状況を写し取ることができます。1人1つまたは2つの競技に出場することから、3つの円が交わっている部分には×印を入れています。

この後、図の各部分をA、B、C、…のような記号でおいて、文字式的な処理をしながら解き進めていくのが現実的なところですが、いずれにしてもほとんどの受験生にとって、試験中に深入りすべき問題ではなかったと思われます。
むしろ、いいタイミングで見切りをつけて、見直しに回ったことが幸いした受験生もいたかもしれません。

合否を分けた一題

2017年度、2018年度と、直近2年間の出題は、JG合格レベルの受験生にとって、かなり易しい内容でした。その傾向が続くのか否かが注目されるところでしたが、本年2019年度の出題は、前年までよりも大幅な難化となりました。

ここ2年とは裏腹に、パッと見て明確な方針が立つ問題が少なく、算数の得意な受験生にとっては、力の発揮のしがいがある試験でした。

逆に、この2年の出題傾向を踏まえ、基本に絞っての対策に留まった受験生には、相当に厳しく感じられたことでしょう。

次年度以降の難易度がどのように推移するのか予測することは困難ですが、今年度の出題を踏まえれば、2016年以前の出題レベルに対応できるだけの対策は必須と言えます。
一方で、易しいセットであったとき際にはミス無くスピード感をもって処理する力も合わせて養う必要もあり、本番では、出題レベルの見極めた上で解答方針を決めることが重要となりそうです。

さて、2019年度の合否を分けた一題としては［５］を取り上げます。

［５］

効率よく処理するためには、数の性質、過不足算、不定方程式（いもづる算）の考え方を柔軟に切り替えながら解き進めることが必要であり、力の差の表れやすい出題でした。

まずは、「12個入りだけにすると菓子は6個余り、15個入りだけにすると菓子は9個余る」という条件に注目してみましょう。
これは、いわゆる「余りの問題」の中でも、差に注目すべき形です。
「12の倍数＋6」、「15の倍数＋9」ではなく、「12の倍数－6」、「15の倍数－6」ととらえることができれば、菓子の個数は、「12と15の公倍数－6」すなわち「60の倍数－6」個であることが分かります。

ここで、菓子の個数が最小である60－6＝54個であるとすると、
12個入りだけ→54÷12＝4あまり6→1500×4＝6000円
15個入りだけ→54÷15＝3あまり6→1800×3＝5400円
より、売り上げの差は6000－5400＝600円となります。

ここに60個の菓子を1セット加えるごとに、
12個入り→→60÷12＝5→1500×5＝7500円
15個入り→→60÷15＝4→1800×4＝7200円
より、売り上げの差は7500-7200＝300円ずつ広がります。

したがって売り上げの差が4500円になるのは、
(4500-600)÷300＝13セット加えたときなので、菓子の個数は、54＋60×13＝834個であると分かります。

この後、売り上げが最大になるときについては、以下のように考えましょう。

12個入りの箱では、1500÷12＝125より、1個あたり125円、
15個入りの箱では、1800÷15＝120より、1個あたり120円
となりますから、売り上げを大きくするためには、なるべく12個入りの箱で売った方が良いことが分かります。

834÷12＝69あまり6より、12個入りの箱は最大で69箱まで用意できますが、そうすると菓子を6個余らせてしまいます。
15個入りの箱も使うことで余りの菓子が出ないように、69箱から1箱ずつ減らしながら調整すると、12個入りの箱を67箱、15個入りの箱を2箱で、菓子を余らせることなく売り切ることができることが分かります。
実際、12個入りの箱69箱で売るよりも、この方が売り上げが多いことが確かめられますので、
（12個入り、15個入り）＝（67箱、2箱）が答えであることが得られました。

はじめから、12個入りの箱と15入りの箱で、1個あたりの金額の差が125-120＝5円であることに注目して解くのも有力です。JG受験生は研究してみると力がつくでしょう。

著者：桑田陽一

この記事は役にたちましたか？