算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

女子学院中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	（１）Ａ　（２）アＡ　イＡ　ウＡ（３）Ａ・Ａ　（４）Ａ・Ａ（５）Ａ・Ａ
［２］	（１）Ａ～Ｂ　（２）Ａ～Ｂ
［３］	B
［４］	（１）Ａ　（２）Ａ・Ａ　（３）Ａ～Ｂ　（４）Ａ
［５］	Ａ～Ｂ・Ａ～Ｂ
［６］	Ａ～Ｂ・Ａ～Ｂ
［７］	（１）Ａ　（２）Ａ～Ｂ・Ａ～Ｂ・Ａ～Ｂ

Ａ：ＪＧ合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、３分以内に解き切る腕力がなければ一旦とばすべき問題

問題別寸評

［１］

例年通りの小問集合です。

（１）計算問題

JGの計算問題として標準的な出題です。
特別な工夫は必要ありません。計算の順序に注意して慎重かつ素早く処理しましょう。

（２）平面図形

正五角形に絡んだ角度の出題です。
正多角形に何本かの線を加えた図形中の角度を求めさせるJG頻出の形ではありますが、今年度の出題は大変容易でした。
正五角形にいくつかの対角線を引いて出来る角度が36°、72°、108°のいずれかであることは、JG受験生ならば頭に入っていなくてはなりません。

（３）売買損益

「定価の100円引きで売ると82円の利益」→「定価で売ると182円の利益」と言い換えることが出来れば、後はそれほど難しい点はありません。JGの売買損益の出題としては平易と言えます。

（４）流水算

流れるプールを題材とした流水算の出題です。
J子さんの速さは「毎分80m＋流速」、G子さんの速さは「毎分70ｍ－流速」と表されますが、この2つの速さの和は、流速が打ち消されて毎分150ｍとなります。
流水上の出会いでは、流速にかかわらず2人の静水時の速さの和を考えれば良いことは練習済みであった受験生も多いでしょう。

（５）平面図形

図1の影の部分に三角形を付け加え、まずは下図の図形の面積を考えると良いでしょう。

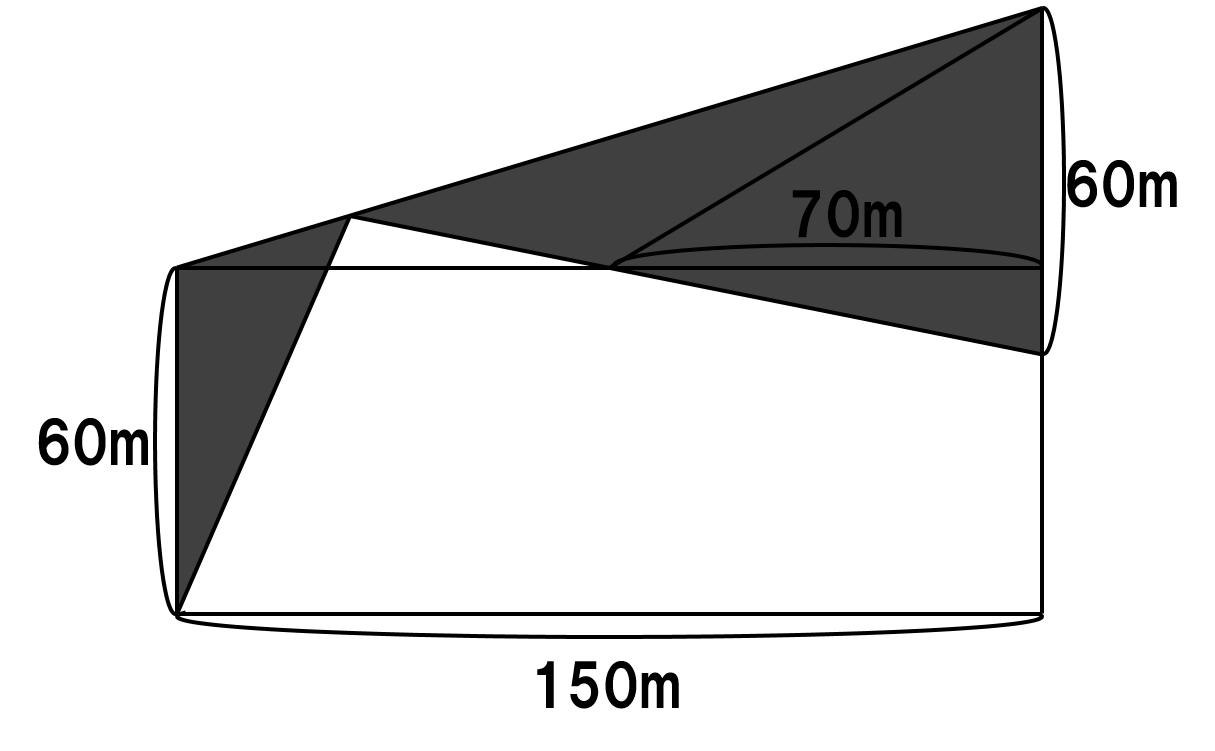
2つの三角形ともに底辺を60ｍと見れば、高さの和が150ｍになっています。よって、この2つの三角形の面積の和は、60×150÷2＝4500㎡です。ここから60×70÷2＝2100㎡を引けば前半の答となります。
前半が分かれば、後半は容易でしょう。

［２］立体図形

直方体と円柱を組み合わせた立体の体積・表面積が題材となっています。JGとしては標準的な難易度の出題ですが、（１）でつるかめ算を利用することにすんなりと気がつくかどうかは受験生の間で差があったかもしれません。そして、（１）が出来れば（２）は比較的容易であるという構成もあわせ、本年度のセットの中では差のついた設問の1つと言えるでしょう。

（１）

直方体の底面積は144cm2、円柱の底面積は78.5cm2で、この2つの高さの和が9cm、体積の和が935.75cm3と与えられています。式にすれば、
（直方体Aの高さ）＋（円柱Bの高さ）＝9cm
（直方体Aの高さ）×144＋（円柱Bの高さ）×78.5＝935.75cm2
と表すことができ、これは典型的なつるかめ算の形になっています。

（２）

（１）を正解できたら、ここは落としたくありません。
求める表面積は、「直方体Aの表面積＋円柱Bの側面積」になっていることを確認しておきましょう。

［３］仕事算

昨年の［１］（６）のように、数学で言うところの「不等式」の考え方を用いる問題でした。今年度のセットの中では、やや考えにくい問題であったと思われます。
合否を分けた一題として、後述します。

［４］数の性質

一見したところ、複雑な条件整理が必要な問題のようにも見えますが、約数の個数と素因数分解の関係を理解していれば、全体に容易な出題です。JG合格レベルの受験生にとっては、充分に練習済みであるはずの内容です。

（１）

題意を確認する設問です。18＝2×3×3と素因数分解して、答を導きましょう。

（２）

「赤に２と書いてある」→「白の数の約数が２個」→「白の数は素数」と、すぐに読み替えられなければなりません。2～41までの整数のうち、素数の個数を数え上げれば、前半部分は解決です。
このうちで緑に1と書いてあるのは、素数であって素因数に2を1個含むもの、すなわち2そのものしかありません。「1枚」が後半の正解ですが、試験場では心理的にやや書きにくい答であったかもしれません。

（３）

問題にある条件を整理すれば、要は、「白の数の約数の個数は８個で、素因数分解したときに2と3の個数はいずれも1個」ということになります。
この条件から、白の数＝2×3×（2、3以外の素数P）と表せることは容易に思い浮かぶところでしょう。
白の数は2～41の範囲にありますので、P＝5以外になく、白の数＝30と分かります。

（４）

「赤に３と書いてある」→「白の数の約数が３個」→「白の数は素数の平方数」というのも、JG受験生には常識でしょう。範囲内にあるのは2×2＝4、3×3＝9、5×5＝25の3つです。

［５］過不足算

「各バスには、先生が必ず2人乗ります。」という条件の処理の仕方がポイントですが、JGの設問として難しい問題ではありません。

乗客55人乗りのバスに乗っている生徒は53人、40人乗りのバスに乗っている生徒は38人ですから、初めから、53人乗りと38人乗りのバスと考えてしまえば、基本的な過不足算として処理できます。

［６］規則性

空きびんを集めてお店に持っていくと、おまけのジュースをもらえるという設定。テキストの標準問題として、一度や二度は練習をしてあるはずの設問です。特にひねったところもありません。

初めは、ジュースを6本買うと、その空きびんを店に持っていくことで1本のおまけがもらえます。このとき、手元におまけの分の空きびんが1本残っているので、その後は5本買うごとに1本のおまけがもらえることになります。
この状況を、「初めから5本買うごとに1本のおまけがもらえて6本飲める」ことにして、「160本のジュース」の代わりに「159本のジュース」として考えると、処理がスムーズです。

前半については、159÷5＝31あまり4より、160本のジュースを買うと、31本のおまけがもらえることが分かります。
後半については、159÷6＝26あまり3より、160本のジュースを飲むためには、26本のおまけをもらえばよいことが分かります。

［７］食塩水

（１）

「食塩水の重さ」を求める場合には、面積図やてんびん図を描いて、逆比を利用するのが定番の解法です。JG受験生としては絶対に落とせない設問です。
(11.2-6.4) : (6.4-2.8)＝4:3より、11.2％の食塩水の重さと2.8%の食塩水の重さが3:4になることを用いて答えが得られます。

（２）

最後の設問！と身構えるほどには難しくありません。流れ図を描いて、丁寧に処理しましょう。

前半について。もともとBに入っていた2.8%の食塩水200gにAから取り出した100gの食塩水を混ぜたところ4.2%の食塩水ができたことから、基本的な計算により、Aから取り出した食塩水の濃さが7％であったことが分かります。
よって、はじめにAにあった11.2％の食塩水を7％に薄めるために、何gの水を加えれば良いかと考えれば、答に至ります。

後半も同様の流れで正解を求めることができます。
現在、Aに入っているのは7％の食塩水が380g。そこに95gの食塩水を加えたところ、6.8％の食塩水になったという条件から、Bから取り出した食塩水の濃度を求めれば、あとは容易に正解できるでしょう。

合否を分けた一題

大問7題構成は2014年度以来。ここ数年少なめに推移していた設問数も28とやや多くなりました。

しかし、全体の難易度はJG合格レベルの受験生にとって非常に易しいものでした。
昨年2017年度の出題もJGとして異例の易しさでしたが、今年度はさらに易しいセットになっています。

合格の力がある受験生であれば、パッと見た瞬間に方針が立たない問題はほとんどありません。方針は立つけど計算が面倒そうだというものも見当たりません。結果として、満点や1問ミス程度の受験生も相当いたことでしょう。ここまで易しいと、算数の力の有無というよりも、ミスの多い少ないが合否を分けた形となっているはずで、算数の力で差をつけたい受験生にとっては、つらい入試となりました。
この2年連続での易しい試験を踏まえ、今後の難易度がどう推移していくのかを予測するのは難しいところですが、現時点では、たとえ2016年以前の難易度に戻っても対応可能なように対策をしておく必要があります。
そして本番で問題を見たときに、全体の難易度を判断してから、処理の方針を決めることが重要になりそうです。

2016年以前のような難易度であれば、限られた時間内での処理スピードと、「捨て問」の見極めが勝負となりますし、昨年や今年度のようなセットであれば、ともかくミスをしないで慎重に解くことが求められます。

どちらのタイプの入試となっても対応できるよう、対策には充分留意して下さい。

合否を分けた一題としては、［３］を取り上げます。

「A11台で仕事をすると、ちょうど3日で終わる」ことから、A1台が1日にする仕事を基準にすると、
A×11×3＝A×33がこの仕事全体の量であることが分かります。

A3台とB2台で仕事をするとき、3日間で行う仕事は、
(A×3＋B×2)×3＝A×9＋B×6
です。
このときまだ仕事が残っているので、これは仕事全体の量であるA×33よりは少なく、
A×9＋B×6＜A×33
⇒B×6＜A×24
⇒B×1＜A×4
となって、B1台がする仕事はA4台分よりも少ないことが分かります。

同様に、A3台とB2台で仕事をするとき、4日間で行う仕事は、
(A×3＋B×2)×4＝A×12＋B×8
です。このときすでに仕事が終わっているので、これは仕事全体の量であるA×33以上であり、
A×12＋B×8≧A×33
⇒B×8≧A×21
⇒B×1≧A× 2018_gouhi_sansu_2
となって、B1台がする仕事はA 台分以上であることが分かります。