算数の合否を分けた一題（2017年度）

算数の合否を分けた一題

女子学院中入試対策・算数の合否を分けた一題（2017年度）

難易度分類

［１］	１）Ａ　（２）Ａ　（３）アＡ　イＡ　（４）Ａ　（５）Ａ・Ａ・Ａ　（６）Ａ～Ｂ・Ａ～Ｂ
［２］	（１）Ａ　（２）Ａ
［３］	Ａ・Ａ
［４］	（１）Ａ・Ａ　（２）Ａ～Ｂ
［５］	（１）Ａ　（２）Ａ
［６］	（１）Ａ　（２）Ａ・Ａ　（３）Ａ/td>

Ａ：ＪＧ合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、３分以内に解き切る腕力がなければ一旦とばすべき問題

問題別寸評

１枚目は例年通りの小問集合。

［１］

（１）計算問題

順算の計算問題。特段工夫は必要ありません。いたって普通の計算です。

（２）平面図形

円周の１２等分点を利用した面積の問題。「円の中心と円周上の点を結ぶ」という補助線の引き方の定石が身についていれば、２つの四分円と２つの直角二等辺三角形に分けることができたはずです。

（３）平面図形

昨年度も出題された、正六角形の分割。
与えられた正六角形の１辺を２としたとき、正六角形全体を「１辺を１とする正三角形」に分けてみましょう。全体が正三角形２４個分、アが５個分になるので、アの面積は全体の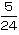とわかります。
角出しを利用するなら、それぞれの面積は、角出ししてできた正三角形が４、アが９－４＝５、正六角形が４☓６＝２４となるので、アの面積はやはり全体の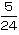とわかります。
イの面積は、全体からア３個分を除いた残りの正三角形の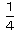になります
アの面積、イの面積、ともに、正六角形の分割としては平易な問題です。

（４）平面図形

平行線にはさまれた等高図形の面積比と底辺比に関する問題。どの塾のテキストでも、例題レベルとして扱われるものです。

（５）平面図形

４問続いた平面図形の小問。最後はＪＧ頻出の角度問題で、受験生にはおなじみの正五角形と正三角形の組み合わせ図形です。底角３６度の二等辺三角形を利用すれば、ア、イ、ウすべての解き方の方針が定まります。JGの角度としては易しく、３つとも完答したい問題です。

（６）不等式

問題用紙１枚目の最後の問題は、数学でいうところの不等式にあたる問題。
後ほど詳しく解説します。

２枚目は大問［２］～［４］。

［２］通過算

２つの列車の追いこしとすれ違いの問題。
列車どうしの追いこしとすれ違いではなく、列車に乗っている人と列車の追いこしとすれ違いなので少々注意すべき点がありますが、ＪＧを目指す受験生にとっては典型題の範疇です。
なお、今年度、「求め方」を要求された問題はこの大問［２］だけで、あとはすべて空欄補充の問題です。

設問（１）は、列車Ａに座っているＪさんが列車Ｂに追いついてから追いこすまでにかかる時間（１２秒）が与えられています。
「距離÷速さ＝時間」の「速さ」にあたるのが「ＡとＢの速さの差」であることは問題ないかと思いますが、「距離」にあたるのが「Ｂの長さ」であることに注意しましょう。

設問（２）は列車Ｂに座っているＧさんが列車Ａと出会ってからすれ違うまでにかかる時間を求める問題です。
設問（１）と同様に、「距離÷速さ＝時間」の「速さ」にあたるのが「ＡとＢの速さの和」であることは問題ないかと思いますが、「距離」にあたるのが「Ａの長さ」であることに注意しましょう。

［３］規則性

規則性の問題と位置付けましたが、複数の解答方針が考えられます。
５９と２２の目もりが重なっている状態から、左側の数字の組合せを順に書き出していくと、（５８，２３）（５７，２４）（５６，２５）・・・。
ざっと考えられる解答方針は以下の３つ。
①はじめの差が３７で、２ずつ差が縮まっていくので、差が１３になるのは（３７－１３）÷２＝１２回縮まったとき、つまり、５９－１２＝４７の目もりのとき。４７－１３＝３４で、組合せは（３４，４７）。
②和が８１になることに気づいたのであれば、和が８１、差が１３で、和差算に持ち込めばOK.。
③このまま書き出して、差が１３になる組合せを見つけてもＯＫ。
どの解答方針をとったとしても、あっさり正答にたどりつける大問です。

［４］時計算

変則時計の問題です。
変則時計というテーマ自体は、開成中、早稲田実業中といった、男子校や共学校での出題が多いという傾向があります。これまで同様の問題を解いた経験があった受験生は、落ち着いて取り組めたのではないでしょうか。
とはいえ、変則時計としては易しい大問です。普通の時計算の仕組みが理解できていることが前提で、この変則時計のルールをしっかり読み取ることができれば、完答できたはずです。

設問（１）は、短針が１周（＝６時間）と５時間ちょっとなので、１１時□分で確定。長針が４の位置にあるので４０分。よって、１１時４０分とわかります。
設問（２）は、午後１時の状態から考えましょう。午後１時のとき、短針は１の位置、長針は６の位置にあり、６０度離れています。普通の時計のときは３０度なので、うっかり間違えないように。
短針の速さは３６０÷３６０＝１度/分、長針の速さは３６０÷６０＝６度/分。
長針と短針の作る角が１８０度になるのは、長針が短針より６０＋１８０＝２４０度多く動いたときなので、２４０÷（６－１）＝４８分より、午後１時４８分とわかります。

３枚目は大問［５］［６］。

［５］売買損益

設問（１）、設問（２）ともに、売買損益の典型題です。

設問（１）は、仕入れ値を１と設定すると、利益が０.１にあたるので、０.１＝３８円より、１＝３８０円。
設問（２）は、問題文を読んだ瞬間につるかめ算とわかったはず。利益だけのつるかめでもよし、売上のつるかめでもよし。利益だけの方が数値が小さくなるので、少しだけ計算がラクになります。

［６］水量変化とグラフ

トリを飾る大問ですが、拍子抜けするくらい易しい問題です。
設問（１）は一見すると判断に時間がかかる問題のように思えますが、実はあっさり判断できます。与えられたグラフの折れ曲がったところの「水面の高さ」が２０cm、６０cm、８０cmであることから、積んだブロックの高さが２０cm、６０cm、８０cmになっている○えが答え。

設問（２）は正面図を描き、底面積、高さ、時間を書き込むことで処理できます。
０～３分後までと３～１３分後を比べて、底面積の比が（３分÷２０cm）：（１０分÷４０cm）＝３：５となり、その差が４００㎠であることから、底面積は１８００㎠とわかります。
水を入れ始めてから３分後までに入った水の量が６００㎠☓２０cm＝１２０００㎤より、１分間に入れる水の量は１２０００㎠÷３分＝４０００㎤。

設問（３）は水量を求めてもよし、正面図で比を利用して考えてもよし。どちらも処理量に大きな差はありません。
後者で解くなら、０～３分後までと１３～○Ａ分後までを比べると、高さは同じ、底面積の比が３：７より、かかった時間の比も３：７になるので、１３～○Ａ分後までは７分間。よって、○Ａ＝１３＋７＝２０とわかります。

合否を分けた一題

まずは、ＪＧの算数を分析するうえで欠かせない総設問数ですが、２０１４年度が３１、２０１５年度が２４、２０１６年度が２５、そして２０１７年度が２２（解答箇所２４）。ここ数年、例年より総設問数が少なめのセットが続いていますが、今年度は特に少ないのが特徴です。

そして、特筆すべきは、難易度。とにかく易しすぎるくらい易しい。少なくとも、直近１０年間の入試において、最も易しい年度であることは確かです。
「標準的なＪＧらしい問題」よりもさらに易しい問題が並ぶ一方で、難易度高めの問題が散見されたのが昨年度のセット。
今年度は、「標準的なＪＧらしい問題」よりもさらに易しい問題が並ぶセット。ひっかかる要素のある問題もほとんど見当たらず、ひたすら“解きやすい”という印象しかありません。冒頭の【難易度分類】について、一部Ａ～Ｂをつけた問題がありますが、例年と比べればすべてＡとしてもおかしくないでしょう。

いつもなら「時間配分と問題の取捨選択」が合否の分かれ目になるのですが、今年度は制限時間内に十分処理できる難易度と分量のセットであったことから、満点に近い勝負といっても過言ではありません。
万が一そのようなセットが出たときの合否の分かれ目が「ミスの有無」であることは、JG志望者であれば散々聞かされていた注意点です。
今年の算数は易しいと気づいた瞬間から、いつも以上にミス防止にアンテナを張って解くことができたか、これが合否の分かれ目だったのではないでしょうか。

前述のように、ひっかかる要素のある問題がほとんどないため、計算ミス、問題文の読みとばし、自分勝手な思い込み、といったミスがなければ、というところです。
ミスが出やすい問題を敢えて挙げるとすれば、各問題用紙の最後に配置されている、大問［１］（６）不等式、大問［４］変則時計、大問［６］水量変化とグラフ。
・大問［１］（６）は、一般的に範囲を問うものを苦手とする受験生が多い
・大問［４］は、変則時計が初見の受験生（そう多くはないはずですが）が慌てたかもしれない
・大問［６］は、設問（１）を間違えると、連鎖的に設問（２）（３）を落とすことになる

このうち、２０１７年度の合否を分けた一題として、大問［１］（６）を取り上げます。

［１］（６）
■「Ａ１個はＢ１個より２７０円高い」
⇒　Ａ☓１＝Ｂ☓１＋２７０円

■「おこづかいでＡを４個買うと３００円余る」
⇒　Ａ☓４＋３００円
＝　Ｂ☓４＋１０８０円＋３００円
＝　Ｂ☓４＋１３８０円　・・・　おこづかい

■おこづかいで「Ｂは６個は買える」
⇒　Ｂ☓２　は１３８０円以内なので
Ｂ＝１３８０÷２＝６９０円以下

■おこづかいで「Ｂは７個は買えない」
⇒　Ｂ☓３　は１３８０円より高いので
Ｂ＝１３８０÷３＝４６０円より高い

よって、　４６０円より高く　６９０円以下

「～より高い」「～以下」という部分で迷いが生じたのであれば、出てきた数値で確かめの計算を行い、問題条件に合致しているか確認してみてください。その習慣がミス防止につながります。

著者：海田真凛

この記事は役にたちましたか？