算数の合否を分けた一題
女子学院中入試対策・算数の合否を分けた一題(2010年度)(2ページ目)
そこで、別の式の作り方をしてみましょう。
つるかめ算の基本「すべて~だったら」の考え方です。
320×ケ + 210×プ + 70×ジ + 120×紅 = 4790 ・・・①
ケ+プ = 13 ・・・②
ジ+紅 = 13 ・・・③
13人ともすべてケーキとジュースにすると
320×ケ + 320×プ + 120×ジ + 120×紅 = 320×13 + 120×13 = 5720
この式から①の式をひいて、実際との差を求めると
320×ケ + 320×プ + 120×ジ + 120×紅 = 5720
- 320×ケ + 210×プ + 70×ジ + 120×紅 = 4790
110×プ + 50×ジ = 930
10でわって
11×プ + 5×ジ = 93 ・・・☆
「 5×ジ 」は5の倍数なので、一の位の数は0か5
すると「 11×プ 」の一の位の数は3か8
よって、プリン = 3または8
こちらの方が、式の処理はしやすいでしょう。先程と同様に、☆の式までたどり着くことができれば答えは求められるはずです。
式の処理だけで☆までたどり着くのは無理という人のために、面積図から☆の式を導く方法がおすすめです。
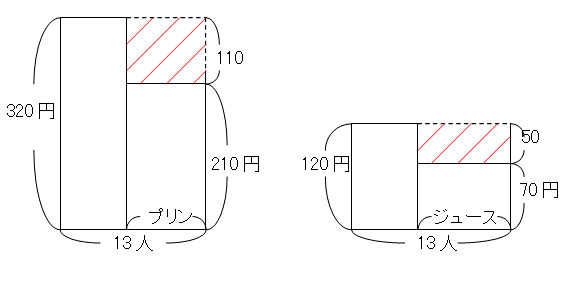
赤い斜線部分の面積の合計は
320×13 + 120×13 - 4790 = 930
赤い斜線部分を式で表すと
110×プリン + 50×ジュース = 930
10でわって
11×プ + 5×ジ = 93 ・・・ ☆
「 5×ジ 」は5の倍数なので、一の位の数は0か5
すると「 11×プ 」の一の位の数は3か8
よって、プリン = 3または8
面積図を書くと問題文の内容を視覚的に捉えることができ、さらに図形問題として捉えることもできるので、式だけで処理するよりも糸口がつかみやすいかもしれません。
この[1](5)は難しい問題ではありませんが、正答率はかなり低かったと思われます。これを2~3分で解き切る力の持ち主は、難なく合格を果たしています。
ただ、この問題を得点できなかったとしても、取りかかってから1分もしないうちに見切って次に進んだ受験生は、時間に追われることなく2・3枚目で得点を重ねることができたようです。逆に、この問題にかなりの時間を費やしたがゆえに、その後の問題に落ち着いて取り組めなかった受験生は涙を呑みました。
各自が明確に時間配分の基準を設けて練習を積み、それを本番で実行できたかが問われる入試だったと言えます。
女子学院中入試対策・関連記事一覧
女子学院中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 時期による算数の学習法の提案(5年生)
- 算数担当講師から女子学院中学入学を目指す受験生へのアドバイス
- 時期による算数の学習法の提案(6年生)前半
- 時期による算数の学習法の提案(6年生)夏休み
- 時期による算数の学習法の提案(6年生)後半
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 算数の合否を分けた一題(2021年度)
女子学院中入試対策・同じテーマ(合否を分けた一題)の記事
- 理科の合否を分けた一題(2010年度)
- 社会の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2011年度)
- 社会の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 算数の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)


 (8 投票, 平均値/最大値: 3.50 / 5)
(8 投票, 平均値/最大値: 3.50 / 5)