算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

本郷入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	(1) A　　(2) A
［２］	(1) A　　(2) A　　(3) A　　(4) A　　(5） A　　（6） A
［３］	(1) A　　(2) A　　(3) A
［４］	(1) B　　(2) B　　(3) B
［５］	(1) A　　(2) B　　(3) C

Ａ：本郷中学合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度・処理量から判断して、得点差がつかない問題

総評

【1】は計算　【2】は1行問題の小問集合　【3】は水量変化　【４】は立体図形　【5】は場合の数および条件整理の出題であり、大問5題、小問17題からの構成でした。【5】の条件整理は考える時間が必要である問題でしたが、全体としてはオーソドックスな問題の出題となりました。難易度は例年よりかなり易化したと言えるでしょう。合格者平均点も74.8点と例年より高く、【１】【２】をしっかり得点し【3】【4】を落ち着いて着手出来れば合格点に届いたと思われます。本郷中学は例年速さや水量変化でグラフの問題が出題されています。日頃からグラフに慣れておきましょう。また、立体図形の切断なども頻出単元であり、日頃から問題を解く際には立体図形の切断面をノートにしっかり書き、練習しておく必要があります。そうすれば十分に対応することができるでしょう。

問題別寸評

【1】計算

(1)逆算。(2)四則演算の基本。
　

【２】

１行問題の小問集合である。ケアレスミスに注意し落ち着いて解答し、全問正解したいところです。
(１)弁償算
もしコインが３０回とも全部表が出たら東へ２４０ｍ。これは実際より１２０ｍ東に進んでいるので　１２０ｍに戻さなければならない。表と裏を１回交換すると８＋４＝１２ｍ西へ戻る。
（２４０－１２０）÷（８＋１２）＝６回→これは裏が出た回数だから３０回－6回＝２４回が表の回数となります。
(２)割合の問題
－２００　：　④＋４００　＝　３　：　４　　　これを解けば　➀＝２５０　２５０×５＝１２５０円

（３）速さの問題
2018_gouhi_sansu_1

（４）いもづる算
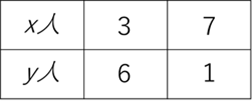
８才の子供の人数をx人,　７才の子供の人数をy人とすると５×x＋４×y　＝３９となるのでいもづる算で考えると右の表のようになります。したがって８才の子供の最大の人数なので　７人となります。
2018_gouhi_sansu_2
（５）場合の数
全員が少なくとも１個はもらえるので、まず７個のうち５個を全員に１個ずつ渡しておきます。残りの２個を５人に配るところを場合分けして考えます。
①異なる２人に２個を配る。→５人の中から２人を選ぶ組み合わせ方と同じです。
５×４÷２　＝　１０通り
②５人のうち１人が２個もらう配り方→５通り
➀と②より１０＋5 ＝１５通りとなります。

（６）
半円の中心が移動したあとを問題文中の図にしっかりと作図してから解くことが望ましいです。
半円の弧が直線AB上を転がるとき、中心の長さは半円の弧の長さに等しいので
４×２×３．１４×１/４×２＋４×２×３．１４×１/2 ＝　８×３．１４　＝２５．１２　ｃｍ

【3】

水量変化の問題。
グラフから読み取っていく問題。オーソドックス問題ですので本郷中合格を目指す受験生なら容易に正解できたことでしょう。
(１)もっとも広い底面積で水が入るとき、100分で１０ｃｍ分水が注がれます。
よって１００ｃｍ×５０ｃｍ×１０ｃｍの水量を１００分で注ぐことになるから、1分あたり１００×５０×１０÷１００＝５００㎤　の割合で注がれます。
(２)右側の部分の高さ４０ｃｍまでは１２０分間で水が注がれるため底面積の横の長さは５００×１２０÷５０÷４０＝３０ｃｍ　よってxは１００－２０－３０＝５０ｃｍ
（３）鉄の円柱の体積は１０００㎤で高さが１０ｃｍであるから底面積は１０００÷１０＝１００㎠

【４】

本郷中の頻出問題である立体図形切断の問題である。必ずマスターしておきたい問題です。
立体の切断の問題は切断面をしっかり作図するところからはじまる。
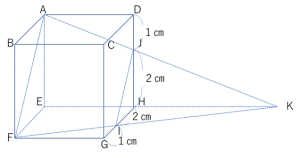
2018_gouhi_sansu_3

切断面である四角形（等脚台形）AFIJの辺AJの延長した直線とFIを延長した直線との交点を点Kとすると、三角すいKAEFができる。
(１)三角形AEFと三角形JHI、そして台形AEHJおよび台形FEHIの面積を求めます。
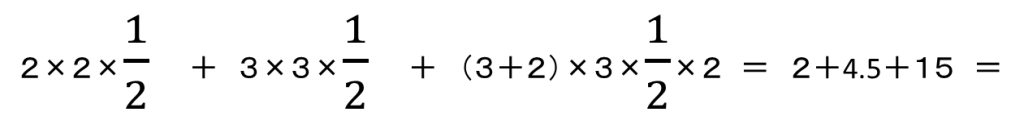2018_gouhi_sansu_4 21.5㎠

(２)対応する頂点の位置を正確に把握し正解したいところです。わかっていてもミスの発生が出やすい問題ですので問題で与えられている展開図上にしっかり立方体の頂点を書き込んでから作図をおこない解答してくだい。

(８)三角すいKAEFの体積から三角すいKJHGの体積をひくことによって求めます。
辺H Kのの長さが求められれば容易に計算できますね。
三角形ADJと三角形KHJが相似であることを利用するとAD ： KH　＝　DJ ： HJ　＝１：　２より、HK＝６㎝になる。
３×３×1/2×（３＋６）×1/3 －２×２×1/2×６×1/3　＝　 2018_gouhi_sansu_5 ㎤

合否を分けた一題

【5】

【5】は昨年同様、先生と生徒との会話が展開され、その会話の内容に隠れている課題を問題として受験生に問うという条件整理からの出題でした。（１）は大小２つのサイコロの目の出方の問題で容易に正解することが出来たでしょう。、（２）（３）は条件整理・推理を必要とするため、解答するのに時間を要する問題でした。今年の【５】はあせって解いてもなかなか正解にたどり着けず、残り時間がなければ飛ばして解答しないという選択もあったのではないでしょうか。ある程度ゆっくり考える時間が確保できれば（２）を正解できた受験生も多いのではないでしょうか。
　
６×６＝３６通り。
（２）例えば出た目の積が５であれば、大小2つのさいころの目は（大，小）＝（１，５）か（５，１）のように１が大のサイコロの目なのか小のサイコロの目なのか確定できません。大,小のいずれの目の数も確定できるのは大小のサイコロの目が両方とも同じ数の目になっている場合のみです。したがって（１，１）（２，２）（３，３）（４，４）（５，５）（６，６）の６通りが考えられますが（２，２）の場合、積が４で（１，４）（４，１）でもよいことになり、積の値から大小の目の大きさがともに確定するという条件にあいません。よって上の６通りから（２，２）を除いた５通りとなります。
（３）大小のサイコロの積と差から大小ふたつのサイコロの出た目の組みを答える問題。
大小のサイコロの目の差は０～５が考えられるが、差が０以外の場合、いずれも大小のサイコロの目なのか確定できません。例えば差が５だとすると2つのサイコロの目は１と６であるが大きいサイコロの目が１なのか６なのかわかりません。差が０であれば大きいサイコロの目も小さいサイコロの目も同じ値ということになります。積が１であれば（１，１）　９であれば（３，３）　１６であれば（４，４）　２５であれば（５，５）　３６であれば（６，６）と大小の目は判明するはずである。積の値を先生におしえてもらった時点でAくんはまだ大小サイコロの目が確定することが出来なかったので
条件に合うのは（２，２）のみである。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？