算数の合否を分けた一題
本郷入試対策・算数の合否を分けた一題(2016年度)
難易度分類
| [1] | (1)A (2)A |
|---|---|
| [2] | (1)A (2)B (3)A (4)A |
| [3] | (1)B (2)C |
| [4] | (1)B (2)B (3)B |
| [5] | (1)B (2)C (3)B |
| [6] | (1)A (2)B (3)C |
A…本郷中合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、後回しにした方がよい問題
問題別寸評
今年は、「2016」の数にちなんだ計算の問題が多くの学校で出題されましたが、本郷も(1)の逆算で出題されておりました。
(1)
2016が含まれる逆算の問題です。整数のみの逆算になるので、必ず得点しておくべき問題です。
(2)
小数・分数の混合問題。引き算、足し算の時は、小数のままが良い場合があり、かけ算・わり算の時は分数でどんどん約分してしまった方がいい場合があります。それを見極めて変形していけば容易に解ける問題です。
一行題の典型問題になります。文章題からは、割合、売買算、つるかめ算、相当算の要素を含む問題。平面図形では、図形の移動、立体からは、水を入れた容器を傾かせる問題というように全てのジャンルからオーソドックスな問題が選出されています。
(1)
個数が絡んだ問題ですが、定価で売った時と、値引きして売った時の2種類がでてくるつるかめ算に気付けば容易に解けるでしょう。
(2)
30ページ読んで5分休むという周期がまずあり、200ページを4時間で読むので、30ページが何回その中に出てくるかを求めましょう。周期算ですが、200÷30=6…
20ページのこの余りの20ページをどう処理するかで解けたかどうかの分かれ目になります。
(3)
これは、円がおうぎ形(四分円)の周りを動いた時の円の通った部分の面積を求める典型問題です。3.14の処理と半径に気をつけていれば簡単に解けるでしょう。完答して欲しい問題です。
(4)
Cを軸に直方体を傾けた時の水の体積を求める問題です。面ABCDに接している水の面積と、傾けた時に同じく面ABCDと接する面積を比べて、比で解いてみましょう。
規則性と植木算の理解を確認する問題です。受験生であれば、紙を何枚か重ねた時の周りの長さや面積を求める問題は解いた事があるでしょう。
(1)
3枚重なっている時の面積が136㎠であるが、おのおの1枚の面積が6×8=48㎠なので、重なっていないとすると48×3=144㎠。よって、144−136=8。8÷2=4。つまり一つの重なっている部分の面積は4。よって4=2×2なので、一辺は2㎝となります。
(2)
実線の部分の周りの長さが問題になっているので、そこに規則性がないかを探りましょう。
つまり、1枚のとき、2枚のとき・・・というように、周りの長さを計算してみると規則性に気付くはずです。
図形が移動する時のグラフの読み取りをさせる問題です。2016年度の問題でおそらくこの[4]が一番手こずる問題でしょう。グラフの一つ一つの区切りに注目して、図形がどの位置になっているのかを読み取る必要があります。ここで時間をかけ過ぎてしまうと残り2問の大問に大きく差がでてきてしまいます。 時間配分の読みが今回はこの[4]にかかっていたように思います。[4]を7〜8分程度でクリアーしたかどうかで合否が分かれたのではないでしょうか。問題の解説は、後述の[合否を分けた一題]で取り上げます。
推理の問題です。条件をしっかりと読み取るようにしましょう。
(1)
B君が学年、C君がクラスの情報を得ている訳なので、まず★のB君が言っている台詞からなぜどちらもわからないのかという事を考えましょう。つまり学年もクラスもわからない状態で、①〜⑩までの情報と、設問にある「5つ」正解になり得ないものがあるという事をヒントに解き進めていきましょう。
(2)
(1)と同様に、B君の台詞から、今度は「学年」のヒントを与えられているB君はわかるけれど、クラスの情報が与えられているC君はまだわからないということは何を意味するのかを考えて下さい。1年生にも2年生にもあるクラスに注目です。
(3)
C君もB君も分かったということは、クラスの情報が一つしかないものです。つまり、①の3組とわかり、学年も分かるということになります。
立方体から3点A,C,Iを通る平面で切りとり、点Bを含む特別な三角すいの体積や切断面を求めさせる問題です。
(1)
切断のルールに乗っ取って考えれば、基本的な問題です。まずは切り口をまちがえないようにしましょう。立方体の外に延びるある1点に集めれば三角すいになります。
(2)
(1)で切り取った、点A,C,Iの切り口の面積を求める問題です。台形になりますが、上底、下底の長さは求められないので、特別な三角すいを用いて面積を出しましょう。
(3)
立方体の外に延びた三角すいの頂点をまず考えましょう。頂点Bから(2)の面に下ろした直線の長さが高さになります。
合否を分けた一題
大問6題のうち、[1]〜[3]までは比較的解きやすい、本郷中を目指す生徒なら必ず解けて欲しい問題になっています。例年、本郷では点の移動や図形の移動でグラフをしっかりと読み取れるかどうかをみる問題が出題されます。今年はそれが[4]に当たるでしょう。良問ですが、図形の位置を正確に把握するのに図を描いてみないとなかなか正解にたどり着けない構成になっており時間を要する問題でした。この[4]に時間をかけ過ぎてしまうと、この後に続く大問2題[5]と[6]で失点してしまうということになりかねません。[5]は推理、[6]は比較的簡単な立体の問題で、失点を避けたい問題です。
時間配分と見切ることのバランスが必要になってきます。そういう意味で、[4]をどう処理するかで今年の合否を分けたのではないかと推測します。
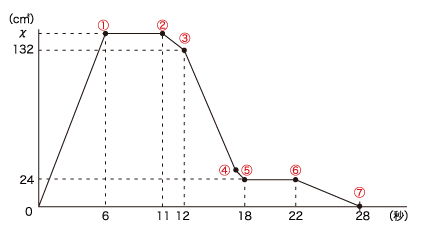
[4]は、図形が動いていく時のグラフの読み取り能力を見る問題です。
まずは、グラフを見ていきましょう。
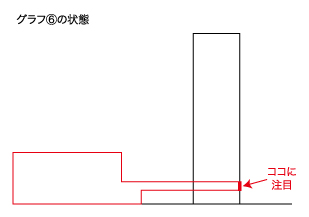
(1)
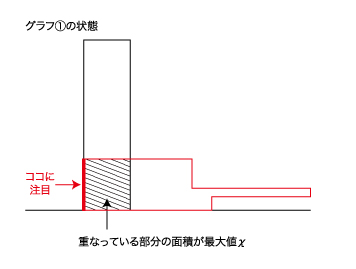
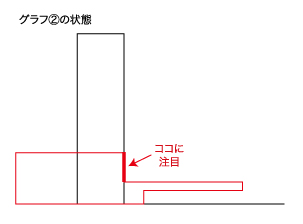
グラフの①と②がAとBが重なっている部分の面積の最大値となっています。
6秒間で最大値となっているので、重なっている部分の横の長さが6×2=12㎝と分かります。また、問題より2つの図形は合同と書いてあるので、重なっている部分の縦もAの横の長さと等しくなります。
よって、12×12=144㎠
(2)
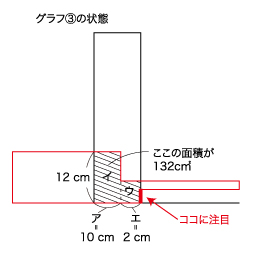
グラフの③の図形に注目してください。重なっている部分の面積が132㎠なので、
11−6=5秒 5×2=10㎝・・・アの長さ
イの面積は12×10=120㎠
ウの面積は132—120=12㎠
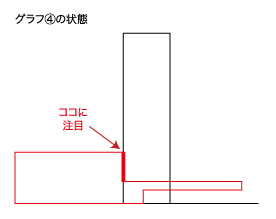
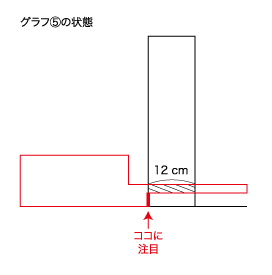
エはグラフの④と⑤の間になるので、1秒×2㎝/秒=2㎝
yは、12÷2=6㎝ 12—6=6㎝
(3)
結局Bは28秒かけてAの図形を通り越しているので、28×2=56㎝
Aの横の長さは12㎝なので、56−12=44㎝
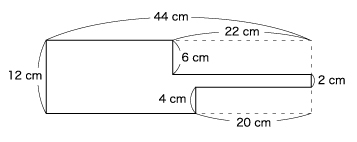
44×12—(22×6+4×20)=316㎠
本郷入試対策・関連記事一覧
本郷入試対策・同じ教科(算数)の記事
本郷入試対策・同じテーマ(合否を分けた一題)の記事
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)