算数の合否を分けた一題
暁星中入試対策・算数の合否を分けた一題（2020年度）
難易度分類
| 大問1 | （１）A （２）Ａ |
|---|---|
| 大問2 | （１）B （２）B |
| 大問3 | （１）B （２）B |
| 大問4 | （１）A （２）B （３）C |
| 大問5 | （１）①A ②A （２）（答）B （理由）B |
A・・・暁星中合格を目指すなら、確実に正解したい問題
B・・・知識、解法次第で、得点に大きく差がつく問題 ⇒ 合否を分けた問題
C・・・難易度、処理量から判断して、正解できなくても合否に影響しない問題
問題別寸評
（１）半径の分からない円の面積の典型題です。確実に正解しましょう。
正方形の1辺の長さが10㎝なので、正方形の面積は100㎠と分かり、正方形の対角線×対角線が200になると分かります。
円の半径は正方形の対角線の半分なので、
半径×半径＝（対角線÷2）×（対角線÷2）となり、半径×半径＝50と分かります。
よって、50×3.14＝157より、157㎠と分かります。
（２）半径の分からない円の面積の典型題です。確実に正解しましょう。
（１）でBDを直径とする円の面積は出ているので、BDを直径とする円の面積の半分は78.5㎠です。そこから（BCを半径とする四分円の面積－直角三角形BCDの面積）を引けば答えが出ます。
よって、78.5－（78.5－50）＝50より、50㎠と分かります。
（１）もとの量が分からないパターンのニュートン算
（２）割合と比
（１）
グラフを読み取って速さの3公式に当てはめるだけです。確実に正解しましょう。
（２）
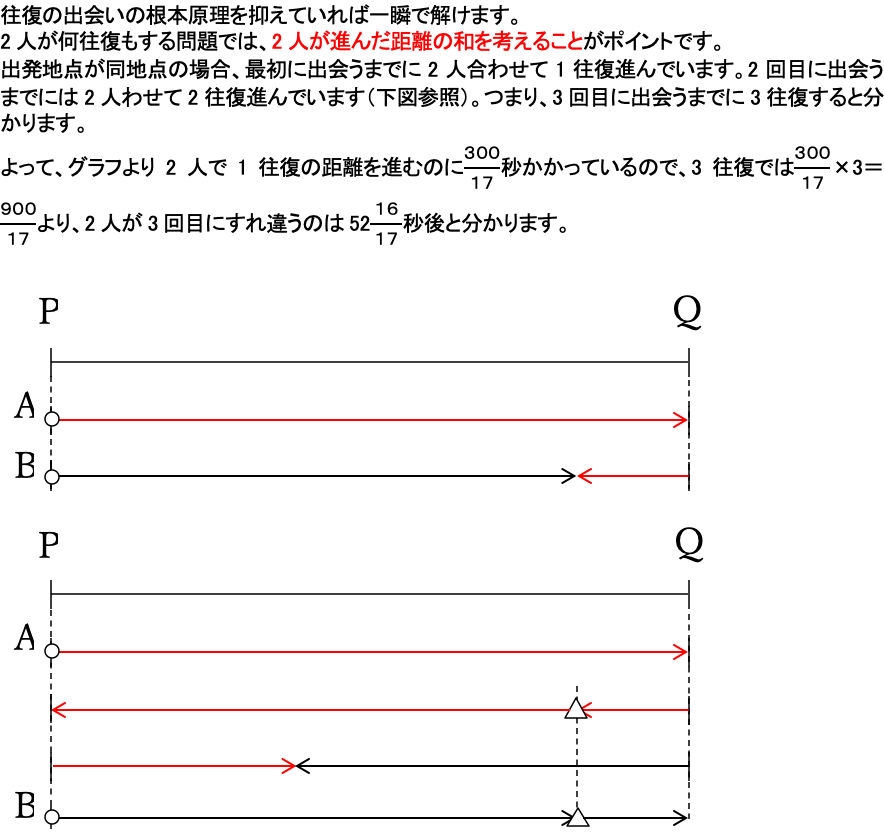
（３）
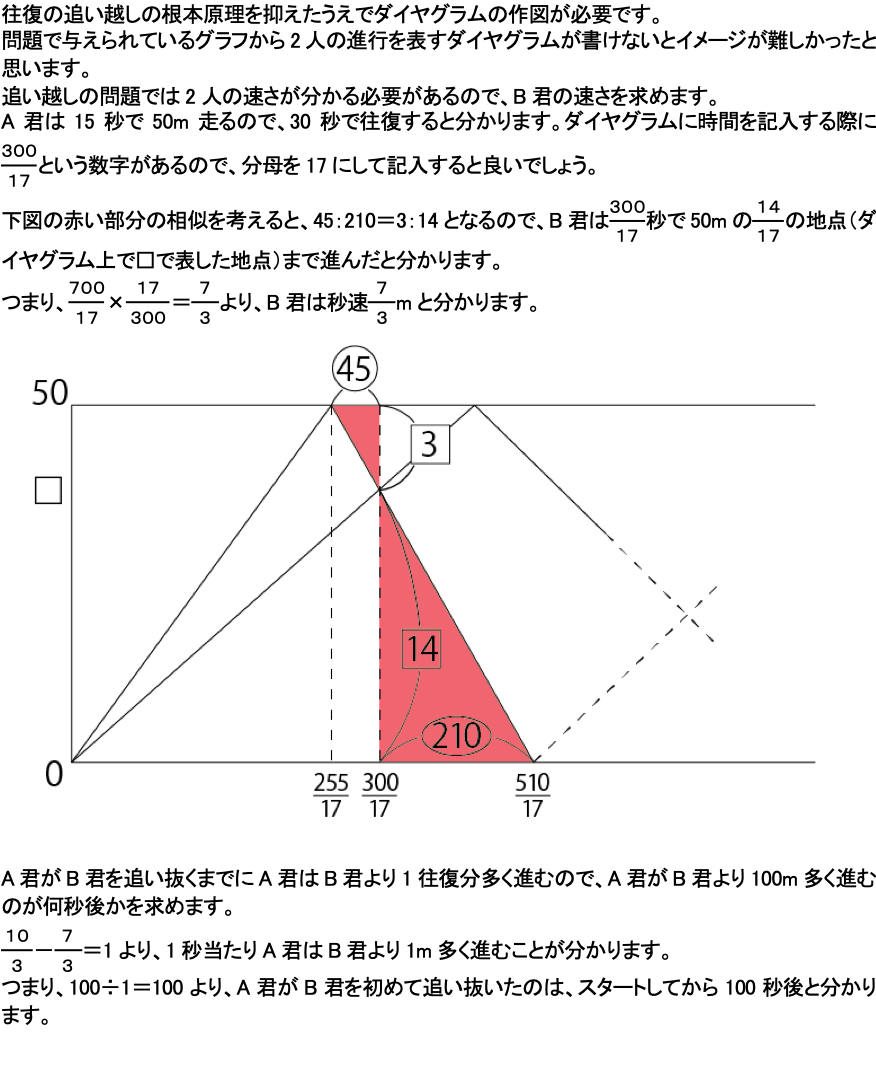
（１）
①②約数の個数を求める問題です。確実に正解しましょう。
単純に1×520、2×260・・・と対となるものを探していってもよいですが、素因数分解をして計算で出すのが1番早いでしょう。
（２）
平方数について答える問題
まず、整数の約数には必ず対となる数が存在します。例えば、6であれば1×6と2×3のように。
そのため、基本的に、ある整数の約数と言うのは偶数個存在します。しかし、本問のように約数の個数が奇数になる数が例外的に存在します。
それは、平方数です。
平方数にも必ず対となる数が存在しますが、平方数とは“同じ数を2回かけてできる整数”ですので、同じ数は約数の個数としては1つとしてカウントされます。
よって、約数の個数が奇数個になるのは平方数と分かります。
合否を分けた一題
この問題は線分図や等式での処理がやや煩雑ですので、情報整理能力がある程度ないと厳しかったと思います。2020年度の第1回入試の問題では大問4の（２）（３）は正答率が低いと考えられますし、大問1、5は割と正答率が高いと考えられますので、大問2または3が合否を分けたでしょう。この2つの中でも大問3は、数字はやや煩雑ですが、どちらかというと典型的なニュートン算ですし、2年連続、大問3でニュートン算が出題されており、対策してきた方も多いと考えられます。ですから、第1回入試ではここ十数年1度も出題されていない、大問2の年齢算が合否を分けたと考えられます。
（１）
数式で処理する年齢算
問題文では、現在と2年後についての情報が与えられており、2年後の年齢に詳しい情報があるので、まずは2年後の状況を線分図で表しましょう。
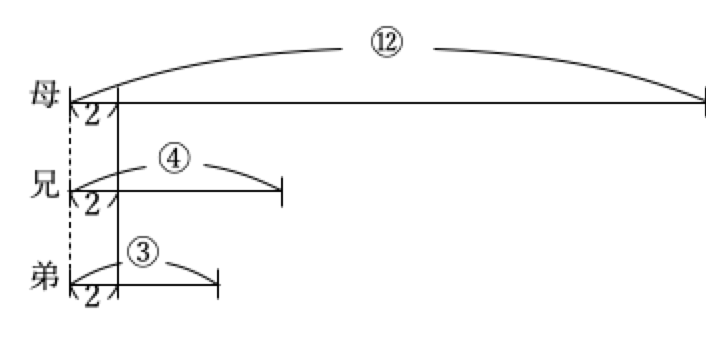
上図のように表せます。すると、現在の母の年齢は（⑫－2）、兄は（④－2）、弟は（③－2）と表せます。ここに、現在の状況を照らし合わせると父の年齢が出せます。
現在、父と弟の年齢の合計は、母と兄の年齢の合計に等しいので、
父＋（③－2）＝（⑫－2）＋（④－2）となります。この式を解くと、父＝⑬－2と分かります。
よって、2年後の父の年齢は⑬、母の年齢は⑫と言えるので、2年後の父の年齢：母の年齢＝13：12と分かります。
（２）
（１）と同じように式処理していきます。
2年後の父の年齢が⑬、弟の年齢が③なので、3年後の父の年齢は⑬＋1、弟の年齢は③＋1となります。
また、問題文より、現在から3年後の父の年齢は弟の年齢の4倍と分かっているので、（１）同様、式で表すと、（⑬＋1）＝（③＋1）×4となります。この式を解くと、①＝3と分かります。
よって、現在の兄の年齢は④－2なので、10歳と分かります。
総評
今年度の入試は大問数、小問数ともに例年通りでした。
また、問題構成も大問1が平面図形の面積、大問3がニュートン算、大問4が速さとグラフ、大問5が数の性質で、去年と全く同じでした。唯一、大問2だけ去年とは異なる分野から出題がありました。また、一昨年も去年とほぼ同じ問題構成でした。
直近の10年分を分析すると平面図形の面積や角度、速さとグラフ、数の性質はかなりの確率で出題されているので暁星の合格を勝ちとるためには必須の分野となります。また、単体での出題はほぼ見られませんが、つるかめ算が速さや仕事算など他の分野との複合問題として出題されることも多いのでそちらも併せて対策すべきでしょう。
(まだ評価されていません)
Loading ...
暁星中入試対策・関連記事一覧
暁星中入試対策・同じ教科（算数）の記事
暁星中入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（算数）の記事
