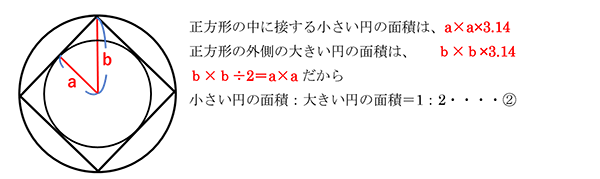算数の合否を分けた一題
暁星中入試対策・算数の合否を分けた一題（2019年度）
難易度分類
| ［１］ | (1)A (2)A |
|---|---|
| ［２］ | (1)A (2)B |
| ［３］ | (1)A (2)A |
| ［４］ | (1)A (2)Ｃ (3)A |
| ［５］ | (1)A (2)B (3)B |
Ａ：暁星合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断してとばすべき問題
総評
昨年と同様に、大問5題、小問12題という出題構成であった。大問1は例年通り
平面図形、大問2は速さとつるかめ算の複合問題、大問3は昨年と同様にニュートン算、
大問4は暁星中頻出のダイヤグラムを要する速さの問題、大問5は数の性質からの出題でした。大問1から大問3まではオーソドックスな問題からの出題であり、暁星中学の受験生であれば十分正解できたのではないでしょうか。大問4は2人の間の距離を表すグラフが与えられており、2人の動きをダイヤグラムに書き直してから考えなければならないため、処理能力が求められる問題でした。大問4の（2）が正解できると（3）も容易に正解できるのですが、（2）で時間をかけすぎた受験生は大問5の題意を読み取ることに落ち着いて取り組めなかったかもしれません。暁星中を目指す受験生は、日頃からダイヤグラムを書いて練習する必要があるでしょう。
問題別寸評
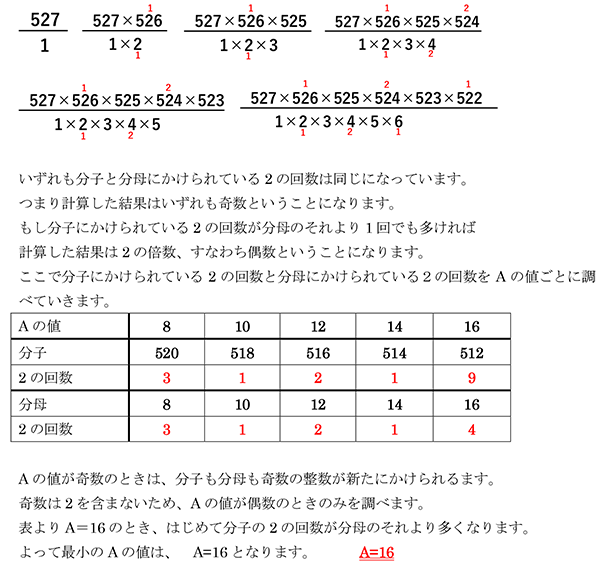
以下の①と②の関係がわかれば容易に解けたのではないでしょうか。
（1）上述の①より、16：1
（2）最小の円の面積と2番目に大きい円の面積の面積比は
上述の②より1：2
さらに2番目に大きい円の面積と最大の面積の面積比は
上述の①より1：4
したがって、最大の円の面積と最小の面積の比は 8：1
（1）はゴールするまでの時間がＢの方がかかるので左曲りの方が
右曲りより長いコースだということに気づけば解ける問題でした。
（2）は平均の速さを用いて、つるかめ算で計算します。
（1）
（2）2人が同時にゴールしたということは、左曲りと右曲りのコースの距離は等しいということがわかる。72/7(㎞/時)と16(㎞/時)、距離の合計10.8㎞、時間の合計58/60時間を用いてつるかめ算で計算すると直線の距離は2.4㎞と算出できる。 2400m
典型的なニュートン算です。時間をかけず、(1)(2)とも正解することが必要です。
（1）平日の1分あたりの来場者数を①人
祝日の1分あたりの来場者数を②人とします。
午前9時の開園時刻に入場ゲートに並んでいる人数は下の線分図で表すことができます。
（2）
2人の距離を表すグラフが与えられている場合、
2人の実際の動きをダイヤグラムに書き直してから考えてみるとよくわかります。
ダイヤグラムに書き直すと、このような図になります
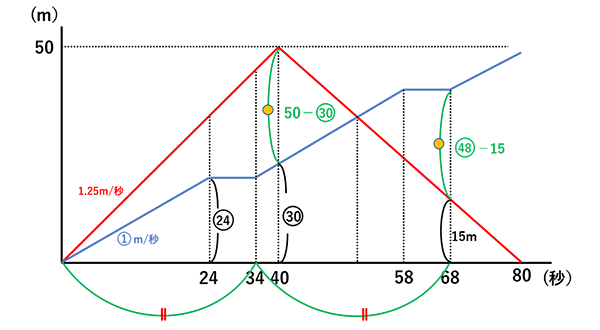
問題で与えられたグラフから
①お父さんの折り返した時間が40秒後であること
②暁くんは泳ぐ時間と休憩する時間を一定の間隔で繰り返すので、
1回目の休憩が終わるのが 68÷2＝34秒後になること
の2点に気づけたかがポイントになります。
（1）50÷40＝1.25m/秒 秒速12.5m
（2）40秒と68秒後の2人の距離が等しいので、
合否を分けた一題で取り上げます。
合否を分けた一題
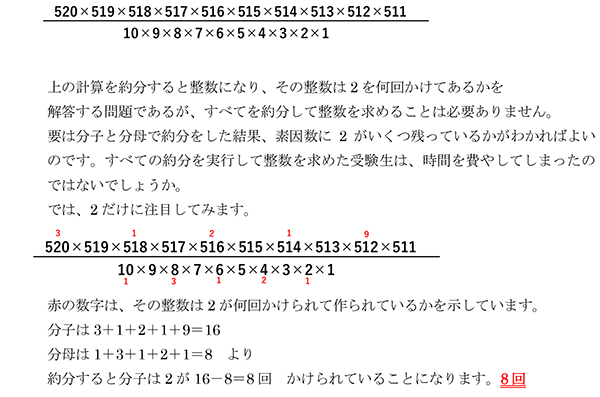
問題自体は難問ではありませんが、問題の題意を読み取ることに時間を要すること、調べるために作業が必要であったこと、全体の最後の出題であったことを考えると、時間切れやあわてていたため得点できなかった受験生もいるのではないでしょうか。題意を理解できた受験生は、少し作業が必要だったとしても得点できたでしょう。一方、調べていく過程で答えは出たが、正解とずれてしまった受験生も多いのではないでしょうか。そういったことから、合否を分けた一題になったのではないでしょうか。
素因数に２をいくつ含んでいるかという問題です。
(1) 512＝2×2×2×2×2×2×2×2×2
よって2が9回かけられています。 9回
(2)
(3) Aの値が A=1 A=2 A＝3 A＝4 A＝5 A=6・・・・となると
それぞれ次のような計算になります。
(1 投票, 平均値/最大値: 5.00 / 5)
Loading ...
暁星中入試対策・関連記事一覧
暁星中入試対策・同じ教科（算数）の記事
暁星中入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（算数）の記事
