算数の合否を分けた一題
暁星中入試対策・算数の合否を分けた一題(2018年度)
難易度分類
| [1] | (1) A (2) A |
|---|---|
| [2] | (1) B (2) B (3) C |
| [3] | (1) A (2) A |
| [4] | (1) B (2) B |
| [5] | (1) A (2) A (3) C |
A:暁星中学合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度・処理量から判断して、得点差がつかない問題
総評
大問5題、小問12題の構成でした。解答は答えだけではなく、記述で解答するため、小問は12問ですが、スピードをもって解答していかないと時間切れになってしまいます。
暁星中学合格を目指す受験生は、日頃から問題を解くときに、記述を意識してノートに解き方を書く練習が必要です。また、大問2で出題された速さの問題では、2点間の距離をダイヤグラムで示された出題であったが、状況を把握するのに考える時間が必要であるため、
一度とばして他の問題を解いてから最後に解くなどといった作戦も必要だったのではないでしょうか。
問題別寸評
面積の求積問題です。正六角形の![]() と
と ![]() の大きさに分けることができれば
の大きさに分けることができれば
求めることができるでしょう。
(1)0.5㎠
(2)![]() ㎠
㎠
合否を分けた一題で解説します。
ニュートン算です。苦手にしている受験生が多い単元ですが、標準的な問題ですのでしっかり練習をして準備しましょう。
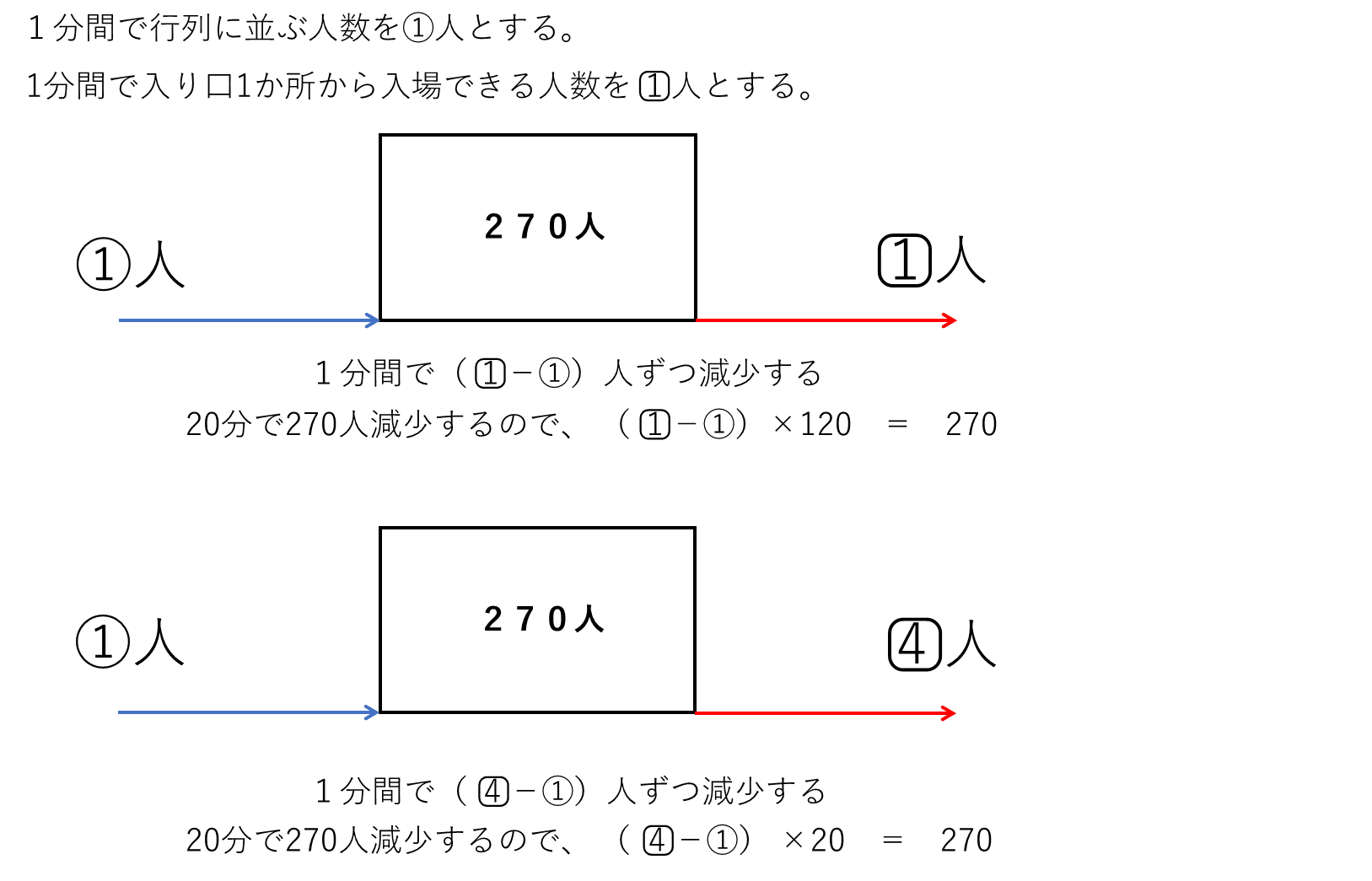

入場口が2か所のとき 1分間で3.75×2-1.5=6人ずつ減少するので、
行列がなくなるのは、270÷6=45分
45分
入場口が1か所のときは、2.25人ずつ行列は減少し、入場口が2か所のときは、6人ずつ行列が減少する。 合計60分で270人の行列をなくすためには、つるかめ算で考えると
(6×60-270)÷(6-2.25)=24分
60-24=36分間
36分間
速さの問題。動く歩道の上を歩きます。
5人分の距離 ÷ (Bの速さーAの速さ) = 15秒
11人分の距離 ÷ (Cの速さ+Aの速さ)
= 11人分の距離 ÷ (Bの速さ+Aの速さ)= 3秒
(Bの速さーAの速さ) : (Bの速さ+Aの速さ) =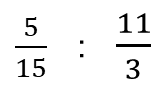 = 1 : 11
= 1 : 11
よって、Aの速さ : Bの速さ = 5 : 6
Bの速さは、分速30 m × ![]() = 分速36 m
= 分速36 m
5人分の距離は、(36-30)×15=90 m ですから、
10人分の距離は、90×2=180 m
180÷(36+36+36×2) = 1.25秒
1.25秒
N進法からの出題です。

(1)7進法で52は、7×5 + 1×2 = 37
37番目

(2)(1)と同様に、
9×9×5 +9×2 +1×0= 423
423番
(3)数列Aのn番目の2桁の数をabとすると、数列Bのn番目の数はbaとなる。
数列Aのab は 7×a + b (番目)
数列Bのba は 9×b + a (番目)
これが、A, Bそれぞれの数列のn番目になるので、7×a + b = 9×b + a となる。
これを解くと 6×a = 8×b a : b = 4 : 3
a, b は 1桁の数字だから、 (a, b) = (4, 3) (8, 6) の2通りが考えられるが、
数列Aは7進法であるので、8は現れません。
よって、a = 4 b = 3 になります。 したがって、7×4+3=31番目
n=31
合否を分けた一題
普通列車と急行列車の先頭がはじめ8300m離れていいるが、普通列車がD駅に、急行列車がA駅に到着するまでに、それぞれ8400 m進んでいるということがポイントです。
状況を把握するまでに計算用紙に整理したりする時間が必要になります。入試問題の2問目にこのような出題があることは受験生にとって選択を迫られることになるでしょう。それは、このまま時間をかけて解答することに突き進むのか、後回しにして、他の解ける問題から解答するのかという選択です。そういった意味で合否を分けた一題になるのではないでしょうか。
2点の距離をダイヤグラムで与えられた速さの問題です。
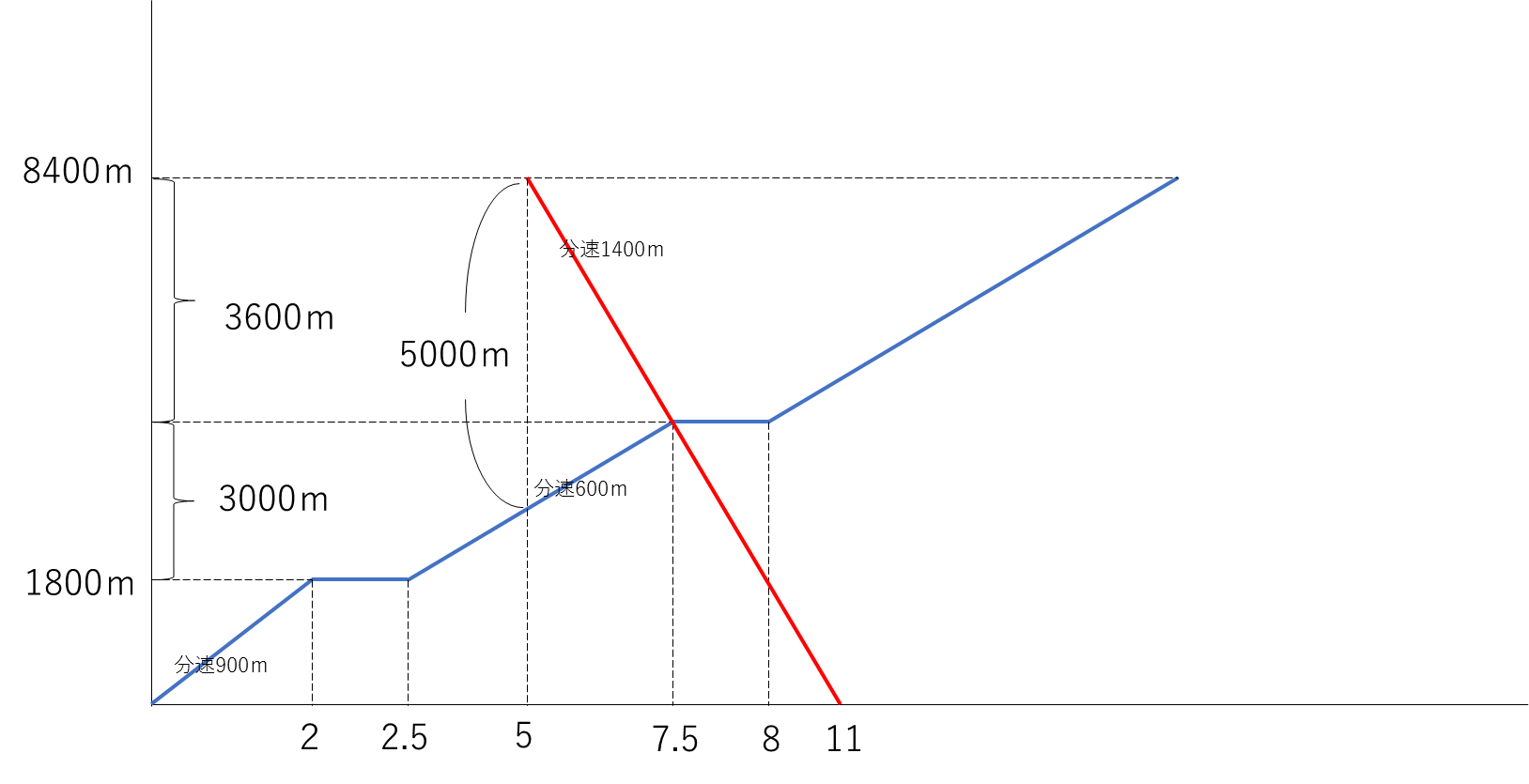
問題で与えられた2点(普通列車と急行列車の先頭)の実際の動きをダイヤグラムで表すと上図のようになります。
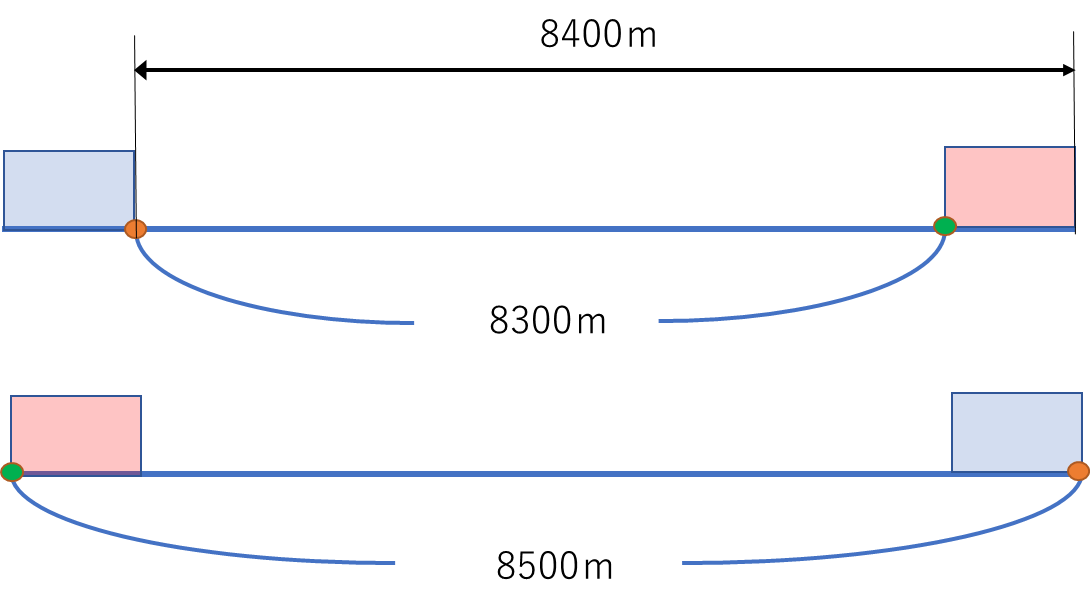
はじめ、普通列車と急行列車の先頭は8300m離れていますが、最後は8500m離れているということに気付けるかどうかかポイントになってきます。
(1)普通列車が出発してから5分後から7.5分後の2.5分間で普通列車と急行列車の先頭は合わせて5000m動いているので、速さの和は
5000÷2.5=2000
よって急行列車の速さは、2000-600=分速1400m
分速1400m
(2)B駅とC駅との距離は、普通列車が出発してから2.5分後から7.5分後までの5分間で移動する距離と等しいです。分速600m×(7.5-2.5)=3000m
3000 m
(3)D駅に到着するまでに進んだ距離は電車の長さを考慮して8300mではなく、8400mであることに気が付けかどうかがポイントです。
8400 m ÷ 分速600m = 14分 B駅とC駅で0.5分ずつ停車するので
14+0.5×2=15
8時15分