算数の合否を分けた一題
暁星中入試対策・算数の合否を分けた一題（2016年度）
難易度分類
| ［１］ | （１）Ａ （２）Ｂ |
|---|---|
| ［２］ | （１）Ａ （２）Ｂ |
| ［３］ | （１）Ａ （２）Ａ |
| ［４］ | （１）Ｂ （２）Ｂ |
| ［５］ | （１）Ａ （２）Ａ （３）Ｃ |
A…暁星中合格を目指すなら必ず得点したい問題
B…着眼点や解法により正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき
問題別寸評
円の面積の出題でした。半径が分からないため、半径×半径に着目して求めるタイプです。
（１）
円の半径は求まりませんが、半径を１辺とする正方形の対角線が６ｃｍであることから、半径×半径＝１８㎠と分かります。
合格レベルの受験生にとっては、易しい問題でしょう。
（２）
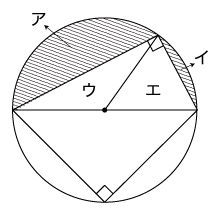
アやイの面積そのものを直接求めることはできません。
「面積の差」を求めるときには、それぞれに等しいものを付け加えて考えるのが定番です。下図のように補助線を入れてみるとウとエの面積は等しいので、ア＋ウとイ＋エ（いずれもおうぎ型）の面積の差を求めればよいことになります。
昨年に引き続き、暁星中で頻出のダイヤグラムによる速さの出題でしたが、本問に複雑なところはありません。ぜひ完答しておきたい大問です。
（１）
ごく基本的な速さの問題です。比例関係に注目してもよいですが、弟の速さを求めて解いても充分です。
（２）
途中で速さが変わっていて全体の距離と時間が分かっているという、典型的な「速さのつるかめ算」です。様子がグラフで与えられていることにとまどった受験生もいたかもしれませんが、内容は基本的で、必ず正解しておきたい問題です。
仕事算の出題です。［２］に引き続いて、つるかめ算の考え方を使います。暁星中の出題としては、たいへん基本的と言ってよいでしょう。
（１）
全体の仕事を１８０分と３００分の最小公倍数の９００と置いてみると、Ａさんは１分あたり５、Ｂさんは１分あたり３の仕事をすることになります。
最後の４５分でした仕事は（５＋３）×４５＝３６０ですから、Ｂさんが１人でした仕事は９００－３６０＝５４０と求められます。
（２）
ＡさんがＢさんに教えながら掃除をしているときの作業量は、問題の条件から、
Ａさん ５×０．９＝４．５／分
Ｂさん ３×１．５＝４．５／分
よって、２人で９／分です。
初めはＢさんが１人で、残りをＡさんがＢさんに教えながら掃除をしたので、３／分と９／分をあわせて１５０分で９００の仕事をしたことになります。あとは、つるかめ算を用いて答えが出ますね。
比の乗除の考え方を用いる問題です。合格レベルの受験生にとっては、充分練習済みの難易度といえますが、受験生間で差が付いた問題だと思われます。
（１）
道のり＝速さ×時間ですから、与えられた比を乗算することにより、
（高速道路を走った道のり）：（一般道路を走った道のり）
＝ ９×５ ： ５×１
＝ ９：１
と求められます。あとは、簡単な計算で答えが出ますね。
（２）
（使ったガソリンの量）＝（道のり）÷（ガソリン１Ｌあたりで走ることの出来る道のり）と表せることに気がつく必要があります。
（１）で道のりの比が９：１であることが分かっていますから、今度は比の除算で、
（高速道路で使ったガソリン）：（一般道路で使ったガソリン）
＝ ９÷６ ： １÷５
＝ １５：２
と求められます。ここまで来れば、あとはやはり簡単な計算です。
整数の積や和が偶数になるか奇数になるかということがテーマです。（１）（２）は容易ですが、（３）の理由をしっかりと記述するのは難しかったでしょう。
（１）
ａ×ｂ×ｃが偶数になるためには、ａ，ｂ，ｃの少なくとも１つが偶数であれば良いですね。このことを確認するだけの設問です。
（２）
（１）と同様、直観的に答えが分かる受験生も多いでしょう。ピンと来なかったとしても、０個のとき、１個のとき、２個のとき、３個のときと順に調べていけば充分です。
（３）
「偶数」になるという結論は多くの受験生にとって容易に得られたと思われますが、理由をしっかりと書けた受験生は多くないでしょう。「合否を分けた一題」で詳しく扱います。
合否を分けた一題
大問５題、小問１１題を５０分でこなすという例年の形式が踏襲されています。
ほぼ全ての問題に途中式や考え方を書くことが要求されていますが、中学受験の算数としては１問にあてられる時間は長めと言えます。
年度によりややバラつきはあったものの、２０１４年までは暁星中の算数といえば、合格者平均点が６割を切ることも珍しくなく、出来る問題を見極めてじっくり解くことが大切な試験でした。算数の得意な受験生にとっては、差がつけやすく力の発揮のしがいのある出題であったと言えるでしょう。
ところが昨年２０１５年の合格者平均点は７５点。差がつきやすい設問であったことに変わりはありませんが、合格水準にある受験生にとってはずいぶん穏やかな出題となりました。
難易度の揺り戻しがあるのか注目された２０１６年度でしたが、結論から言えば昨年並みかそれ以上に穏やかな出題となりました。正答できなくてもやむを得ないと言い切れる問題は最後の小問である［５］（３）のみ。もちろん、合格のために他の問題を全て正解する必要があるわけではありませんが、２０１４年以前の出題では困難なレベルの高得点をたたき出した受験生も多かったと思われます。
２０１７年以降、同様のレベルの出題が続くか、２０１４年以前のレベルに戻るのか、どちらに転んでも対応できるよう充分な対策が必要です。
さて、「合否を分けた一題」として、上記の［５］（３）を取り上げます。
「偶数」になるという結論を得ることは、それほど難しくないでしょう。例えば、ア、イ、ウ、…、ソに順に１、２、３、…、１５を当てはめてみるだけでも分かります。しかし「どのように入れたとしても」偶数になる理由をきちんと記述するのは、中学受験生にとってはやや難しかったかもしれません。
与えられた式は全体が積の形になっているので、（１）をヒントにすると、
１＋ア、２＋イ、３＋ウ、…、１５＋ソ
の全ての和の値が奇数でない限り、与えられた式の値は偶数になることが分かります。
さて、全ての和の値が奇数になるようにア～ソに整数を当てはめることは可能でしょうか？
２つの整数の和が奇数になるのは、奇数＋偶数（または偶数＋奇数）の場合です。
１～１５の整数には奇数が８個で偶数が７個ありますから、奇数８個にはそれぞれ偶数を、偶数７個にはそれぞれ奇数を組み合わせなければなりません。
つまり、ア～ソには偶数が８個、奇数が７個必要になりますが、ア～ソも１～１５の整数をでたらめに１つずつ入れたものなので、偶数は７個、奇数は８個です。
以上のことから、全ての和の値を奇数にすることは不可能であることが分かりました。
したがって、与えられた式の値は「偶数」です。
理由や考え方を説明させる問題は、暁星中では数年に１回のペースで出題されています。以上の内容を自分で答案の形にまとめてみる練習は、良い対策となるでしょう。
(1 投票, 平均値/最大値: 1.00 / 5)
Loading ...
暁星中入試対策・関連記事一覧
暁星中入試対策・同じ教科（算数）の記事
暁星中入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（算数）の記事
