算数の合否を分けた一題
慶應普通部入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| [1] | ①B ②A |
|---|---|
| [2] | ①A ②A |
| [3] | A |
| [4] | A |
| [5] | B |
| [6] | B |
| [7] | B |
| [8] | ①A ②B |
| [9] | B |
A:慶応普通部部中合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、飛ばすことも考慮すべき問題
問題別寸評
① 計算問題
素因数分解を活用すると手早く処理できました。
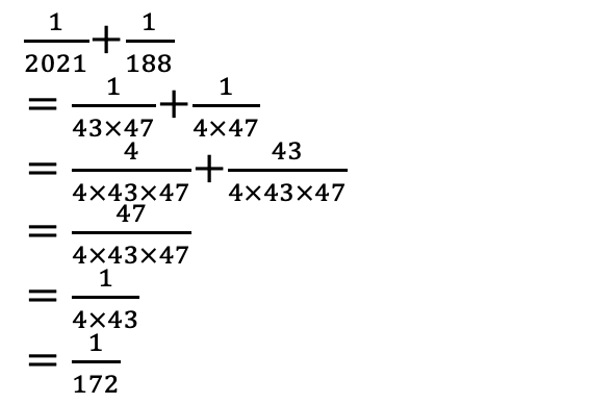
より、□=172でした。
② 計算問題
逆算の計算問題です。標準的な難易度の問題です。
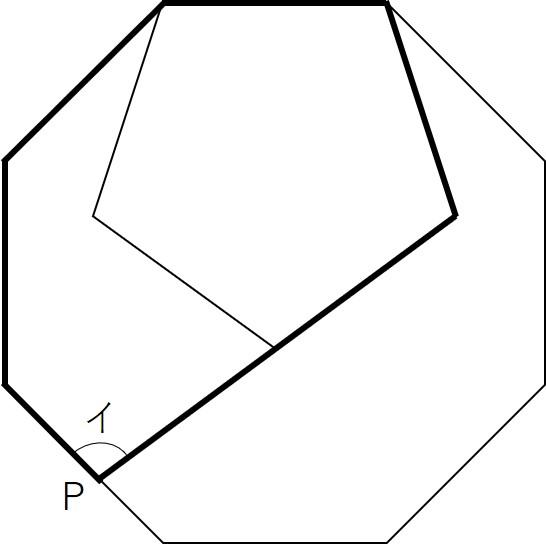
[2] 角度
①②正多角形と角度の問題でした。アの角度は多くの受験生が正解したと思われます。イの角度も図の太線の六角形に気付けば早かったのではないでしょうか。
[3] 逆比
等しいものを探し、AとBとCの残金の比を出すことが出来れば正解までたどり着けたはずです。確実に正答したい問題でした。
[4] 場合の数
これも標準的なカードの並べ替えの問題でした。3の倍数を作る問題では、使用する数の組み合わせを考え、その後並べ替えという手順となります。
やや複雑な問題でした。後ほど合否を分けた一題で取り上げます。
B、C、Dの大小を仮定し、4つの数の合計が40という条件をもとに解き進めます。とりあえず作業してみる、書き出してみるという習慣のある受験生は問題なく処理できたと思われます。
①
標準的な難易度の問題です。相似比と面積比の関係を捉えられる受験生であればスムーズに処理できたはずです。
②
①の解答の4:1をそのまま用い、「底面積の差=側面積の差」で式を立てる方法が最も素早く処理できるのではないかと思われます。方針を素早く立てることが出来るかどうかで、所要時間に差が生まれたと予想できます。
①
山道の問題の定石で、図の点線のように補助線を引くことが出来れば難なく正答にたどり着けるはずです。
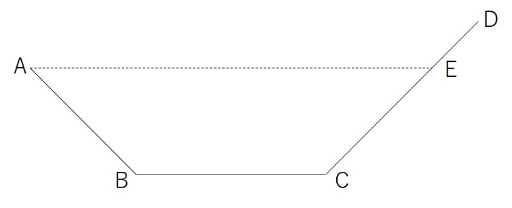
②
太郎君がAB間を移動するのにかかる時間と、次郎君がEC間を移動するのにかかる時間は同じです。「次郎君が図のDE間を移動する時間、太郎くんに平地を移動させる」と考えることが出来ればスムーズに解ける問題でした。
様々解法はあるでしょうが、図のように角出しし、比の合成を行うのが一般的ではないでしょうか。
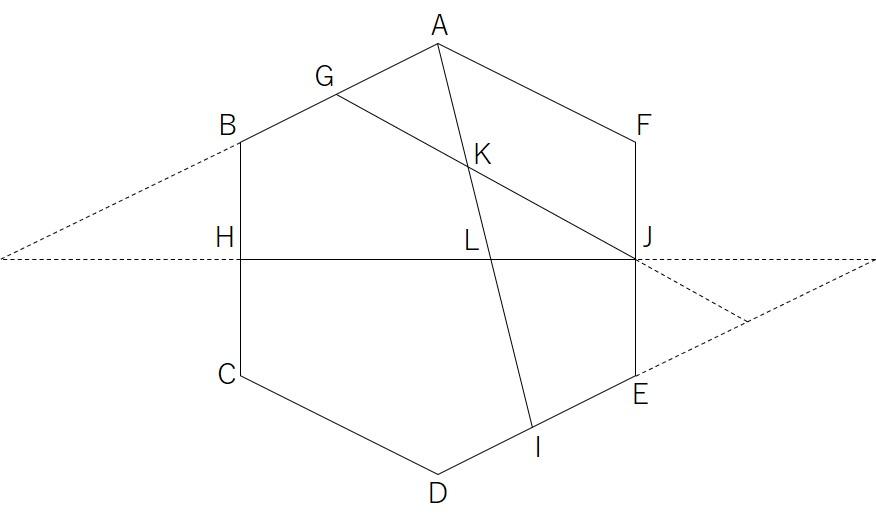
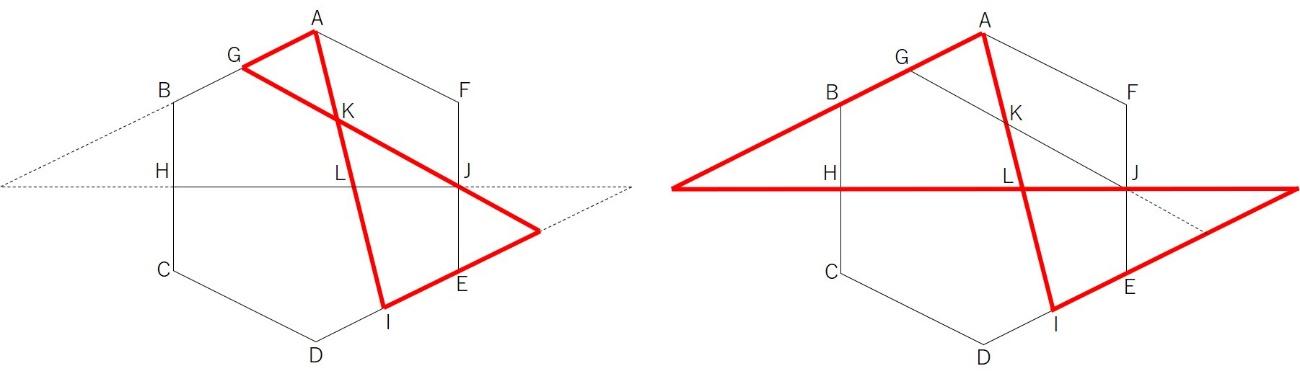
普段の学習内容とも共通点があるので考えやすかったと思われます。
合否を分けた一題
2021年度は難易度・問題数ともに大きな変化は見られませんでした。どこかで一度見たことがあるような問題が多いですが、細部に変化球的な要素があり、方針を立てるのに手間取ってしまうとあっという間に40分の試験時間は無くなってしまいます。
受験生の間で差がつく可能性があるのは、やや珍しい範囲を求める問題であった大問[5]、試行錯誤が必要な大問[6]、方針を立てるスピードで差がついたと思われる大問[8][9]です。この中から、合否を分けた一題として大問[5]を取り上げます。
2500個のキャンディを3個ずつ配って500個以上余る、という条件から子どもの数は最大で
(2500-500)÷3 = 666・・・2
より、666人とわかります。
次に子どもの最小人数についてです。キャンディを3個ずつ配ったあと、余ったキャンディを追加で1個ずつ配るということは、全員に4個配るのと同じことです。結果、80個以上キャンディが不足しました。ということは、1人に4個ずつキャンディを配るのであれば、最低でも2500+80=2580個のキャンディが必要です。よって、子どもの最小人数は2580÷4=645人となります。
最大値については手早く処理出来た受験生が多かったと予想されます。一方で、最小値については問題文の表現にかなり混乱した受験生も多かったのではないでしょうか。
慶應普通部入試対策・関連記事一覧
慶應普通部入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 塾ごとの算数の学習法の提案(日能研生)
- 算数担当講師から慶応普通部入学を目指す受験生へのアドバイス
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
慶應普通部入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2010年度)
- 国語の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2021年度)
- 理科の合否を分けた一題(2021年度)
- 国語の合否を分けた一題(2021年度)