算数の合否を分けた一題（2020年度）

難易度分類

１	（１）Ａ　（２）Ａ　（３）Ａ
２	（１）A　（２）A　（３）A
３	Ｂ
４	Ｂ
５	（１）Ａ　（２）Ａ　（３）Ｂ　（４）Ｂ
６	（１）Ａ　（２）Ｂ　（３）Ｃ
７	（１）Ａ　（２）Ｃ　（３）Ｃ

A…慶應普通部合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

出題総評

慶應普通部の入試には目立った傾向がないと言われることもありますが、しっかりと分析していけば、年度によらず出題されている、根本的な考え方の傾向があります。

①場合分け・分類の力
②複雑な旅人算・状況図の作図による整理
③比を利用した消去算
④直角三角形の相似・縦横比
この４つのポイントについては、例年出題されており、今年も出題されていました。直近５年で同様の問題が出題されている際にはその問題番号を各問題の解説の冒頭に併記しておきます。
慶應普通部中学の隠れた傾向を把握し、学習を進めてください。

問題別寸評

大問１

（１）

部分分数分解を利用する問題です。

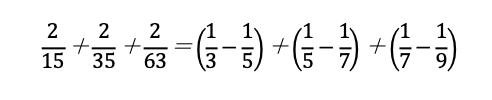
のように変形して、計算を楽にするテクニックです。入試では頻出ですので、しっかりと身に着けておきましょう。

（２）

0.625という数の並びを見たら、即座に5/8が思い浮かぶでしょう。

大問２

【出題傾向③比を利用した消去算】
同様の根本原理を用いた類題
2019年3番
2018年4番
2016年2番
2015年5番

問題文で２つ以上の比が示され、それらを具体的な数値と組み合わせて答えを導く問題です。
同様の形式の問題は慶應普通部で頻出です。

特徴としては、具体的な数（～人や～mなど）を用いて、何かの具体的な数値を求める問題が多いことです。
具体的な数が示されない形式の「AはBの何倍ですか」のような出題は少なくなっています。

２つ以上の比が示されている場合には、解法は、「消去」と「比合わせ」の２つに大別できます。本学では「消去」の解法を用いる問題も多く出題されていますが、2020年度入試の本問は「比合わせ」を用いる問題でした。

大問３

平行四辺形に何本か線が引かれていて、長さの比を求める問題です。
女子校では鴎友中学などで頻出の形です。多くの中学校の入試で頻出の問題ですが、慶應普通部では比較的珍しい問題です。

解法としては、相似形を作るために、下の図のように延長した補助線を引いて考えることが良いでしょう。

大問４

【出題傾向②複雑な旅人算・状況図の作図による整理】
2019年4、
2018年8、（ダイヤグラム付き）
2016年3（ダイヤグラム付き）
2015年9

慶應普通部では、２人が２点間を往復するような、動きの複雑な旅人算の問題が頻出です。
問題の中にダイヤグラムが示される年もあれば、ない年もあります。2020年はダイヤグラムなしの流水算でした。

状況図を描くやり方と、ダイヤグラムを描くやり方があります。
慶應普通部の出題傾向を分析すると、状況図で十分解ける問題が多くなっています。
ダイヤグラムの作図が苦手な受験生でも、状況図で解くことが可能です。

状況図を描く際に気を付けるポイントとしては、「時間一定」の根本原理を利用するために「同時刻マーク」を書き入れることや、「距離一定」を利用するために同じ地点を点線で結ぶことなどがあげられます。
地味なようですが、状況図の適切な描き方は必ず練習しておくべきです。

その他本問の細かいポイントとしては、AとBの２つの船が川を往復するため、速度の変化でミスをしないようにする必要があります。

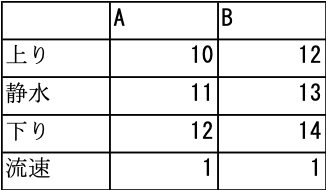
上のような表を書いておき、すぐに判別できるようにすると良いです。

大問５　虫食い算の問題です。

２×□＋□□－60÷□
の□に、３から６の書かれた４枚のカードを入れて、計算の答えを最大にするという問題です。
２×A＋BC－60÷D

の、どこに最大の数字「6」を設置するのが最も効率が良いのか。次に大きな数字「5」はどこに設置するのか。
例えば、Aの位置を5にする場合と6にする場合では、計算結果に2の差が出ます。一方で、Bの位置を5から6にすると、10も大きくなります。同様に、Dの位置を5から6に帰ると、2の差が出ます。
以上のことから、最大の数字である「6」は、Bの位置に設置するのが最も効率が良いということになります。
このように当てはめて考えることで、最大の数字を求めていきます。

大問６

【出題傾向④直角三角形の相似・縦横比】
同様の根本原理を用いた類題
2019年7（立体の切断）
2016年8（方眼紙のナナメの線。縦横比）

慶應普通部の隠れた出題傾向としては、直角三角形の相似があげられます。
なぜなら、相似の中でもこの直角三角形の相似は最も発見しづらいのです。
相似の問題で、よく見る形は「ピラミッド型」と「砂時計型」の２種です。この２種については、受験生は多くの問題で練習しています。
しかし、この「直角三角形の相似」については手薄になっていることがあります。

例えば立体の切断という単元では、実はこの直角三角形の縦横比が頻繁に使われます（切断面を図示する際に、立体における平行線を引く手順があり、ここで使われる考え方です）。
2016年の方眼紙の問題と2019年の立体切断の問題は一見全く違う単元に思えますが、その裏にある考え方は共通しています。
2020年度入試の6番でも、この直角三角形の相似の考え方が用いられています。

【合否を分けた一題】

大問７

【出題傾向①場合分け・分類の力】
同様の根本原理を用いた類題
2019年5
2018年5、9
H28年4
H27年4、7

慶應普通部の最大の特徴である「場合分け・分類の力」を問う問題です。
「～通りですか」や「全て答えなさい」といった出題形式にすることで、場合分けして調べる力や、特徴的なポイントに注目して分類する力を試しています。

例年、この出題傾向①に相当する問題は１～２問出題されていましたが、2020年度入試では、大問7・8・9が全てこの傾向に該当する問題で、なんと3問も出題されていました。
慶應普通部を目指す受験生にとって、このポイントを習得することは必須といえるでしょう。

それでは、本問の背景の解説に移ります。
平面図形の典型問題で、「多角形に対角線は何本引けますか」という問題があります。
この問題には公式があり、n角形であれば
（n－3）×n÷2
で求められます。
例えば８角形であれば
（8－3）×8÷2＝20
より、20本と求められます。

さて、多角形の対角線の本数を求める公式は、多くの受験生が覚えているでしょう。本問は、さらにその先を問いかけています。
つまり「なぜその公式が成り立つのか、理由まで理解していますか？」ということを試すために、立体図形の対角線という形式で出題しているのだと思います
その先で、先述した「場合分けする力」が求められてきます。

平面図形の対角線について、根本原理から理解している子にとっては、この問題は難なく解けたでしょう。「あの問題と同じだ」くらいに思ったかもしれません。
しかし、公式を丸暗記していたり、根本原理の理解が不十分な受験生にとっては初見の問題に思えてしまい、解けないか、又は時間が多くかかってしまうことが予想されます。

普段からの学ぶ姿勢を受験生に問うている良問という点で、本問を、合否を分けた一題とします。

以下で解説していきます。
展開図を組み立てると、下の図のようになります（受験生も、解答用紙や問題用紙の余白に、この図を書くと良いでしょう）。

各頂点から対角線が何本引けるか、を考えていきます。
この図形には9つの頂点があります。
例えば点Oについて考えてみると、隣接した点であるA～Dには対角線は引けません（隣接した点同士を結んだ線は「辺」になってしまいます）。
また、自分自身、OからOにも、当然引けません。
よって、9つの点から、隣接した4つと自身の1つ、合計5を引いて
9－5＝4　本の対角線を引くことができます。

よって、図の点Oからは、４本の線が引けます。
他の点についても同様に考えていくと、
図の点Aからは、4本の対角線が引けます。これは、点B～Dについても同じです。
図の点Eからは、5本の対角線が引けます。これは、点F～Hについても同じです。

これらを合計すると、
4＋4×4＋5×4＝40　となります。

このように、9つの頂点を場合分けして考えることが必要です。

大問８

【出題傾向①場合分け・分類の力】
同様の根本原理を用いた類題
2019年5
2018年5、9
H28年4
H27年4、7

並べ替えの問題です。
本学で出題される場合の数の特徴としては、場合分けの書き出しと順列計算の両方が必要となる問題が多いということです。

出題傾向にあるように、何に注目して場合分けするのが良いのか。分類の力が試されています。
本問は、1,1,1,1,2,2,2,3の8枚のカードを、となりのカードと数が異なるように並べる並べ方は何通りあるかという問題です。

まず、1のカードに注目して分類します。
考えられる場合分けとしては、
1□1□1□1□
□1□1□1□1
の２通りです。

このように場合分けすることで、残った２と３のカードを入れる入れ方が何通りあるかをそれぞれ考えれば良いことになりました。
場合分けと分類というポイントに注目しましょう。

大問9

【出題傾向①場合分け・分類の力】
同様の根本原理を用いた類題
2019年5
2018年5、9
H28年4
H27年4、7

この問題の本番は、(2)の7mの時です。どのような手順で調べ上げていくのが良いのか。組み合わせを書き出し、次に順列を考えるという基本手順が身についている受験生とそうでない受験生の間で差が出る問題です。

(1)4mのひもを切り分ける組み合わせを書き出し、その並び替えの数を考えていきます。
3,1・・・2通り
2，2・・・1通り
2,1,1・・・3通り
1,1,1,1・・・1通り

より、7通りです。

(2)7mのひもの場合について、4mの時と同じように考えていきます。
書き出す際に、自分の中で「ルール」を設定します。今回は、大きい数字を左に書くというルールで書き出します（反対に、小さい数字を左に書くというルールでも構いません）。自分の中でどちらかに統一して書き出すことが大切です。

3,3,1・・・3通り
3,2,2・・・3通り
3,2,1,1・・・12通り
3,1,1,1,1・・・5通り
2,2,2,1・・・4通り
2,2,1,1,1・・・10通り
2,1,1,1,1,1・・・6通り
1,1,1,1,1,1,1・・・1通り

より、答は44通りです。

まとめ

慶應普通部の問題は、試験時間が短いこともあり、思考力というよりは処理スピードを問う問題だ、と一般に言われることもあります。
しかし実際はそうではなく、本学の入試には思考力が必要です。
試験時間内だけではなく、普段の学習の際に、しっかり考えて勉強しているかが問われています。
塾で公式や解法を習った際に、どうしてそうなるのか。その根本の理由まで深く考えていることが、本学の入試問題を解く鍵となります。
一見シンプルな問題でありながら、その実、日頃の思考の深さを問うているという点で、
非常に良質な入試問題を出す学校です。

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？