算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

慶應普通部入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	①A　②A
［２］	A
［３］	A
［４］	B
［５］	B
［６］	B
［７］	A
［８］	①A　②C
［９］	A
［１０］	①A　②B

Ａ：慶應普通部合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき

出題総評

今年も、例年通り大問10題構成となり、40分という短い時間の中で、どの問題を取捨選択するか？という判断力が問われる試験となりました。ただ、昨年度よりも全体的に問題の難易度が易化したと言えます。
大問１は計算２問、大問２は底辺比と高さ比を利用した平面図形の問題、大問３は円を転がす図形問題、大問４は立式をしていく割合の文章題、大問５は２つのサイコロをふる場合の数の問題、大問６は立体の個数を考える図形問題、大問７は同時の発車時刻を考える数の性質の問題、大問８は速さとダイヤグラムの問題、大問９は道順を考える場合の数の問題、大問１０は切断した立体図形の問題でした。

問題別寸評

[１]

①　答　１０４０
全てではないが、一部で工夫を利用する計算問題。１４×（１２＋１６）＋１８×（１６＋２０）とまとめると良いでしょう。

②　答　 2018_gouhi_sansu_01
分数と小数の入り混じった逆算。式の中で、先に計算できるところ（９．６× 2018_gouhi_sansu_02 の部分）はして、丁寧に一つずつ逆算していくようにしましょう。①も含め、この大問１で時間をかけることは許されません（２問で２～３分程度が望ましい）。

［２］

答　１０３㎠
平面図形の底辺・高さと比あわせを利用した求積の問題。まず、平行四辺形ですのでADとBCは等しく、AE：ED=３：５、BG：GC=７：５。次にそれぞれの合計が８と１２なので、最小公倍数の２４に比を揃えます。同様に、AH：HB=２：１、DF：FC=３：２で、それぞれの合計の３と５の最小公倍数の１５に比を揃えます。
ここまでの条件を整理すると、以下のようになります。
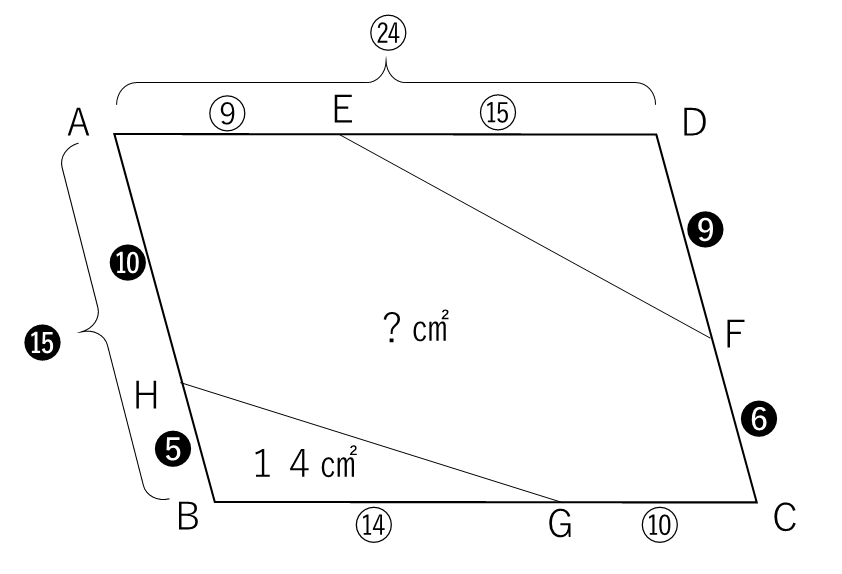
2018_gouhi_sansu_03
三角形HBGは⑭×❺÷２＝３５＝１４㎠です。
また、平行四辺形ABCDは㉔×⓯＝３６０、三角形EDFは⑮×❾÷２＝６７．５となるので、六角形AHGCFEの面積はABCDからHBGとEDFを引いて求まります。

［３］

答　２５１．２㎠
特定の図形の周りに、円を転がして通った軌跡の面積を求める問題。まず、その様子を作図すると以下のようになります。
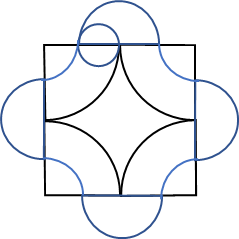
2018_gouhi_sansu_04

求めるべきものは、
と 2018_gouhi_sansu_06 が４組分となります。あとは計算して答えが求まりますが、円周率の３．１４は最後にかけるようにしましょう。

［４］

答　２３５人
３種類の部屋の数を比でおいて、一部屋当たりの人数と部屋の数をかけ合わせたものが合計の人数であることを利用した割合の文章題。立式をしっかりしていくことが大事です。
Aの数を②、Bの数を③、Cの数を⑤とおくと、生徒全員の人数は問題文前半の条件から５×（②＋③＋⑤－３）と表せます。また、問題文後半の条件から６×②＋５×③＋４×⑤と表せます。あとは、それらを整理して①がいくらかを求め、生徒全員の人数を計算していくだけです。

［５］

答　１３通り
今年も出題された、条件整理をする場合の数の問題。今年は本問を、合否を分けた一題として詳細を後述します。

［６］　

答　８個
立方体が何個か積んであり、その２方向から見た時の投影図から個数を推測する立体の問題。上から見た図をベースにし、正面・右方向から見た時の個数を書き加えると以下のようになります。
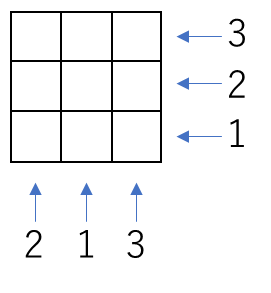
2018_gouhi_sansu_07
個数が少なくなる場合を考えるので、正面と右で数字が被るところをその個数にします。（以下参照）
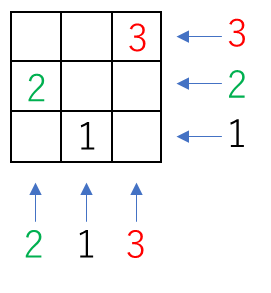
2018_gouhi_sansu_08
ところが、この状態だと問題文の「面と面がぴったり重なるように…」という条件に当てはまらないので、条件に適するように最小の個数で配置すると以下のようになります。
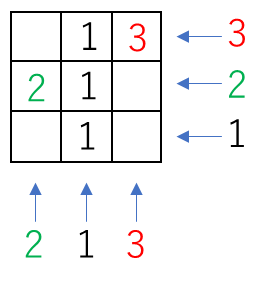
2018_gouhi_sansu_09

［７］

答　午前１０時１０分
電車・地下鉄・バスが同時に出発する時刻を、倍数の考え方から求めていく数の性質の問題。
３つの条件を同時に考えるのではなく、まずは電車・地下鉄と２つで考えます。
書き出していくと午前５時２２分に重なり、それ以降は１６と１２の最小公倍数である４８分ごとに同時出発します。調べていくと、１回目に３本が同時出発するのは午前６時１０分です。求めるのは２回目なので、１６・１２・２０の最小公倍数をさらに考えて計算すると答えが求まります。

［８］　本校ではお馴染み、複数の登場人物が出てくる速さとダイヤグラム作成の問題。②は計算が煩雑なので後回しにすべきですが、本校の対策をしてきた受験生としては①のダイヤグラム作成は失点できません。

①答
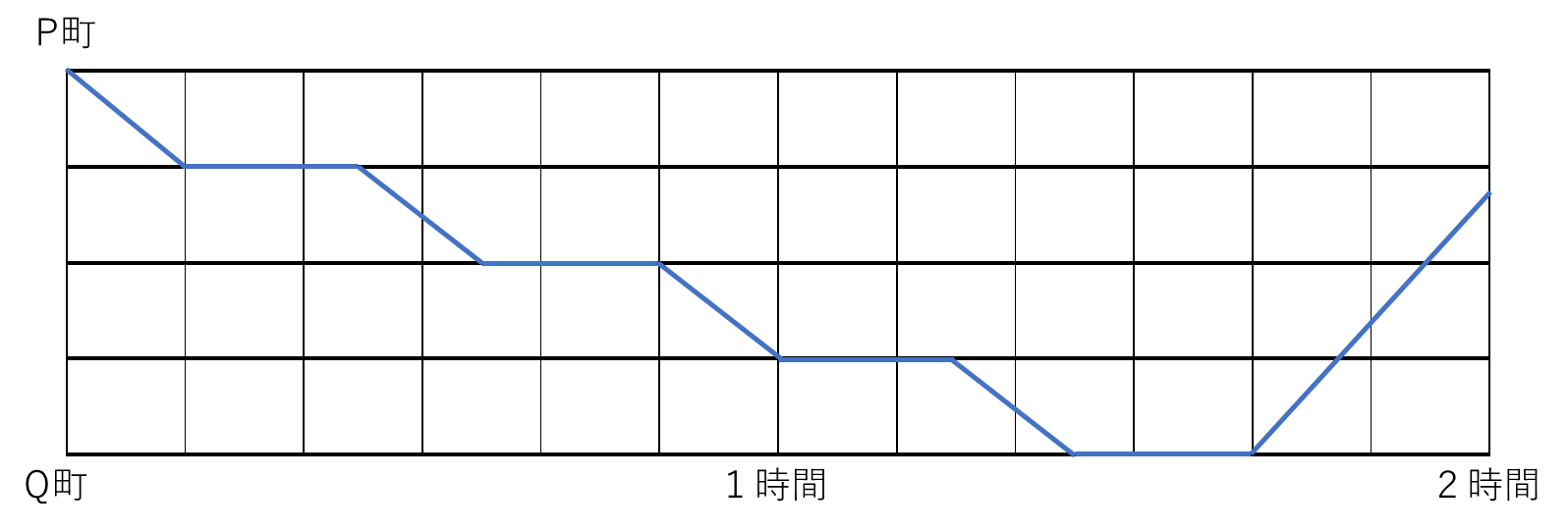
2018_gouhi_rika_1s
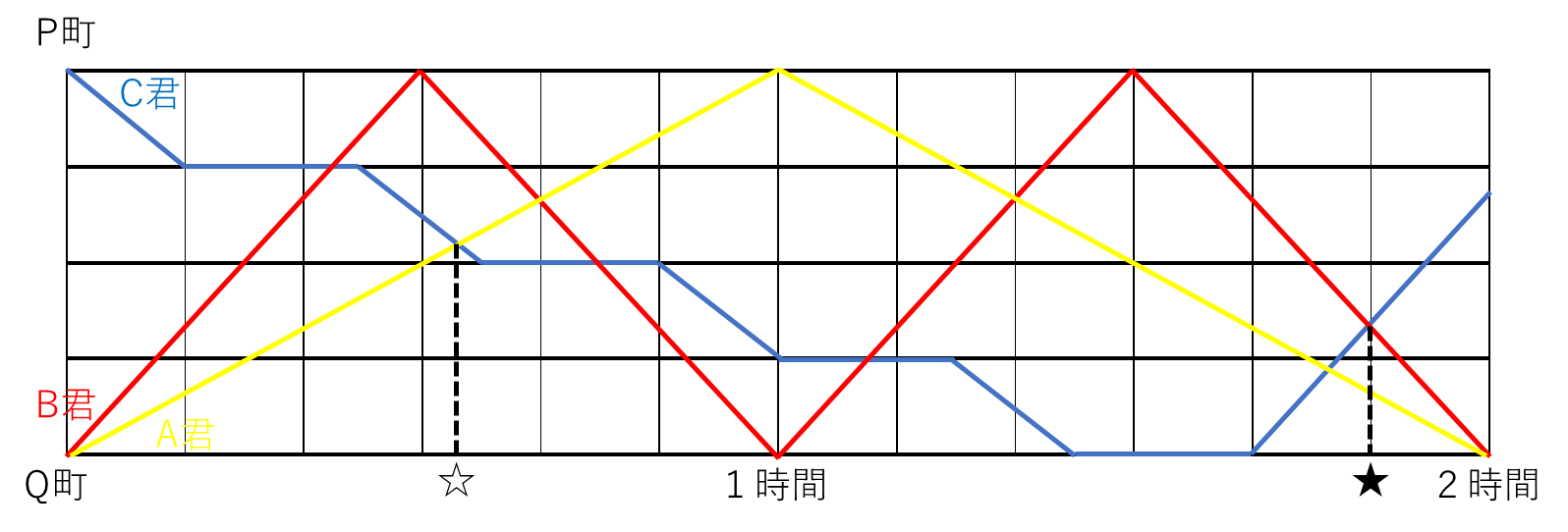
まず、PQ間は４ｋｍ／時×１時間＝４ｋｍです。C君は１時間２５分＝８５分で移動し、１ｋｍ進むごとに休憩を取るので、４回進み、３回休憩を取ることになります。したがって、８５－１５×３＝４０分で４ｋｍを進むことになり、速さが求まるのでグラフが上のように描けます。

②答　1時間17分
３人の情況をグラフにすると、以下のようになります。
2018_gouhi_rika_2s
2018_gouhi_rika_3s

［９］

答　10通り
拍子抜けしてしまうくらい、単純な道順の問題。そもそも、答えが少ないです。樹形図を描いて調べていけば答えが求まります。本問は、絶対に落としてはなりません。一つだけ注意点として挙げるなら、問題文の例（A⇒B⇒C⇒F⇒E⇒D）も含めるように。

［１０］

立方体から三角錐を複数切り取った図形問題。本校のみならず、出来上がった立体の見取図は他の問題でも目に触れたことでしょう。この問題も落とせません。

①答　１４４０㎤
元の立方体は１２×１２×１２＝１７２８㎤。また、切り取った立体は、１つあたりが底面を１辺が６ｃｍとした直角二等辺三角形であり、高さが１２ｃｍの三角錐です。その体積が６×６÷２×１２÷３＝７２㎤なので、立方体の体積からそれを４つぶん引けば答えが求まります。

②答　７２０㎠
表面積の問題は、方向によって面積を分けるように。
上…対角線がどちらも１２ｃｍのひし形（正方形）なので、７２㎠。
下…一辺が１２ｃｍの正方形なので、１４４㎠。
前、後、左、右…たて、よこ共に１２ｃｍの三角形なので各々が７２㎠。
ななめ…先述した三角錐の断面積は、その展開図を描くと下の三角形ABCになります。

１２×１２－（１２×６÷２×２＋６×６÷２）＝５４㎠となり、それが４面ぶんあることになります。
あとは、全ての面積を合計すれば答えが求まります。

合否を分けた一題

今年の慶應普通部の算数は、例年と同じように割合の文章題・速さのダイヤグラム・立体図形といったお馴染みの問題以外に、明らかに平易な道順の問題も目立ちました。昨年よりもさらに、４０分という短い時間の中で、どの問題に何分の時間を費やし、どれだけより他の受験生よりも高得点を取れるか、という姿勢が強く問われた試験だと言えます。
今回は、前半の問題群の中で大問５の数が絡んだ場合の数の問題を、合否をわけた一題として紹介しましょう。

［５］場合の数

まず、２つのサイコロに大小の区別があることに注意が必要です。問題文の条件から出た目がともに偶数の場合は、得点は偶＋偶。それ以外は得点が偶×奇・奇×奇となりますが、６の倍数になる時なので奇×奇はありえません。２つの場合について整理して考えてみましょう。
① 偶＋偶の場合
和が６⇒（２，４）で２通り
和が１２⇒（６，６）で１通り
合計３通りです。
② 偶×奇の場合
積が６⇒（２，３）で２通り　（６，１）で２通り
積が１２⇒（４，３）で２通り
積が１８⇒（６，３）で２通り
積が３０⇒（６，５）で２通り
　合計１０通りです。
よって、３+１０=１３通りとなります。
答え：１３通り

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？