算数の合否を分けた一題
雙葉中入試対策・算数の合否を分けた一題(2021年度)
難易度分類
| [1] | (1)A (2)A (3)A (4)A |
|---|---|
| [2] | A |
| [3] | (1)A (2)A (3)A |
| [4] | A |
| [5] | (1)A (2)①A ②B |
A:雙葉合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題 ➡ 合否を分けた一題
C:難易度や処理量から判断して、部分点狙いで答案を作成すべき問題
問題別寸評
(1)計算問題
逆算です。素直な数値なので、確実に得点すべき問題です。
(2)食塩水
加水なので、①てんびんや面積図で解く、②食塩の重さが変わらないことを利用して解く、どちらでも構いません。
(3)平面図形
今年度の平面図形は超典型題。半円とレンズ型の組合せ図形です。円周率が3.14なので、4個のレンズ型の合計面積は「1辺10cmの正方形の面積×0.57」で求めることができます。
(4)通過算
これも通過算の典型題の組合せです。
列車が2種類のものを通過したとき: 差をとって、距離の差÷時間の差=列車の速さ
列車どうしの追いつき: 列車どうしの長さ和÷速さの和=追いついてからおいこすまでの時間
の2点をおさえていれば解けます。
ここから問題用紙2枚目です。
「残りの1/4」「残りの半分」……と下に線分図をおろして解き進めていく相当算。これも典型題。
(1)
「今日は昨日の4%減の人数」という割合の基本問題。
(2)
複数の解法が考えられますが、昨日と今日の「中人+大人」の2式を立て、消去算に持ち込むのが最短距離の解法でしょう。
(3)
大人と中人の入場料を丸数字で設定し、マルイチ算で解くのが無難です。
ここから問題用紙3枚目です。
正四面体の展開図が下図のように2種類しかないことを知っていればラクに解ける問題です。
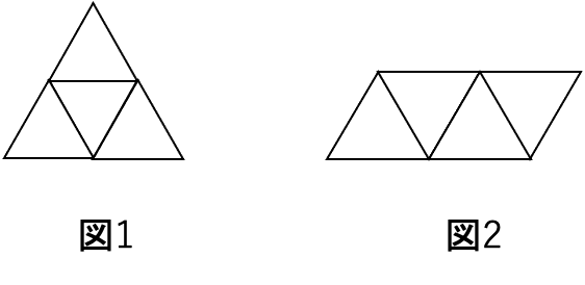
図1のタイプは、真ん中が色つきでそれ以外が白の場合と、真ん中が白でそれ以外が色つきの場合の2通り。図2のタイプは、色つきと白を交互に並べる1通り。あわせて、全部で3通りです。
知識の有無により所要時間、正答率に差がつく問題といえます。
水そう問題ですが、仕事の問題として全体量設定からスタートし、最後は比例式、倍数算的な式処理や比合わせ、等、複数の解答方針が考えられます。このあと詳説します。
合否を分けた一題
2021年度は、過去20年間を遡っても例を見ないほど易しいセットです。ほぼ雙葉算数の頻出テーマからの出題ですが、どれも典型題の枠を出ず、見慣れた問題ばかり。解き進めていくうちに、あまりにも易しすぎて、本当にこれでよいのだろうか、何かひっかけがあるのではないかと、余計な不安を抱いてしまうほどです。
これだけ平易なセットだと、上記【難易度分類】でのA問題をノーミスで確実に得点し、2問しかないB問題で勝負、という構図になります。
この2問のうち、比の文章題としてとらえることができれば処理方法の幅が広がる[5]の最終設問(2)②を今年度の合否を分けた一題として取り上げます。
(2)②の設問を解くために、設問(1)と(2)①で得た情報を確認しておきましょう。
(1)

(2)①
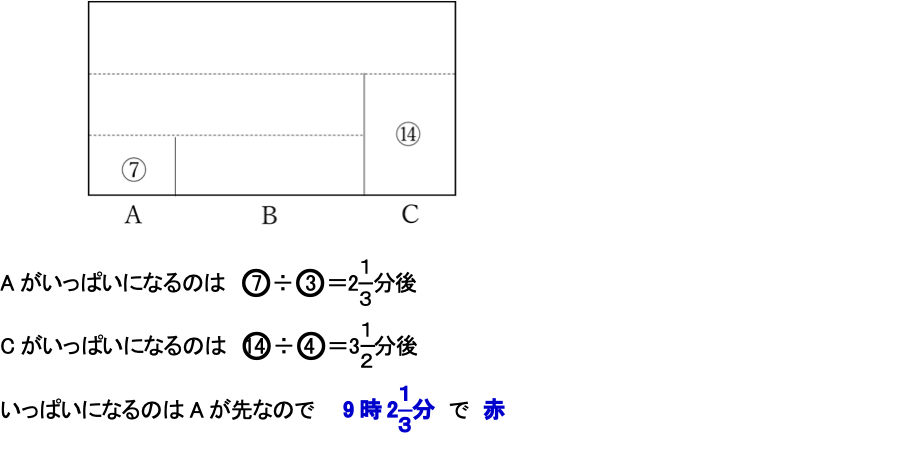
(2)②
どの状態から考えるか?
・・・はじめから, Aがいっぱいになったときから, Cがいっぱいになったときから
どのような処理方法に持ち込むか
・・・比合わせ, 比例式, 倍数算的処理etc.
選択次第で、その後の計算量と数値の煩雑さに差が出ます。
ここでは、計算の分量をおさえるという観点から、はじめの状態から考えて、比例式で処理します。

雙葉中入試対策・関連記事一覧
雙葉中入試対策・同じ教科(算数)の記事
- 算数の出題傾向分析
- 算数の合格戦略の提案
- 算数の合否を分けた一題(2010年度)
- 時期による算数の学習法の提案(5年生)
- 時期による算数の学習法の提案(6年生)夏休みまで
- 時期による算数の学習法の提案(6年生)秋以降
- 塾ごとの算数の学習法の提案(サピックス生)
- 塾ごとの算数の学習法の提案(日能研生)
- 塾ごとの算数の学習法の提案(四谷大塚生)
- 算数担当講師から雙葉中入学を目指す皆さんへアドバイス
- 算数の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2014年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
雙葉中入試対策・同じテーマ(合否を分けた一題)の記事
- 算数の合否を分けた一題(2010年度)
- 理科の合否を分けた一題(2011年度)
- 算数の合否を分けた一題(2012年度)
- 理科の合否を分けた一題(2012年度)
- 算数の合否を分けた一題(2013年度)
- 理科の合否を分けた一題(2013年度)
- 社会の合否を分けた一題(2013年度)
- 国語の合否を分けた一題(2013年度)
- 算数の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2019年度)
- 国語の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2021年度)
- 社会の合否を分けた一題(2021年度)