算数の合否を分けた一題（2020年度）

算数の合否を分けた一題

雙葉中入試対策・算数の合否を分けた一題（2020年度）

難易度分類

１	（１）A　（２）A　（３）A
２	Ｂ
３	（１）A　（２）B
４	（１）A　（２）A　（３）B
５	（１）A　（２）A　（３）B

A…雙葉合格を目指すなら、確実に得点したい問題
B…解法や着眼点次第では、得点に差がつく問題
C…難易度、処理量から判断して、部分点を拾えれば良しとする問題

問題別寸評

演習量を重ねてきた受験生にとっては、過去にどこかで見たことのある問題が多く、「この問題は◯◯に注目すべき問題かな」と、方向性がつかみやすいものが多かったのではないでしょうか。
ただし、最後の大問５が、雙葉らしい「計算力と根気」が必要な問題だったので、最後まで気を抜かずにどの程度得点できたかが合否を分けたことでしょう。
のちほど、合否を分けた一題として取り上げます。

１

(1)

分数・小数を含んだ一般的な逆算の問題です。
確実に正解しましょう。

(2)

時事ネタといってもよい「軽減税率」の要素を取り入れた割合の問題でした。
ただ、特にひねりのない問題でしたので、やはりこれも確実に正解しなければなりません。

(3)

リングをつなぐ規則性の典型題です。
1個3.5㎝のリング1964個ぶんの長さを求め、あとで重なり部分を引いて求める方法（植木算の考え方）もありますが、1個だと全体の長さは3.5㎝、その後1個付け足すごとに全体の長さは2.5㎝ずつ増えるという、等差数列の考え方を用いる方が汎用性は高いです。
どちらの解法を用いても構いません。この問題も確実に正解したいところです。

２

問題文を読んだとき、「どのように計算していけばいいのだろう」と、一瞬とまどった受験生も多かったかも知れません。
2月1日から4月30日までの日付の数字すべての和から、月曜日から金曜日以外（すなわち土曜日と日曜日だけ）の日付の数字の和を引いて求めればよい、とすぐに気付けるかどうかが最大のポイントだったと言えるでしょう。
また、問題文にも丁寧に書かれていますが、2020年はうるう年なので2月は29日まであることにも注意が必要です。

３

(1)

正十角形の1つの内角を求めることができれば、二等辺三角形に注目し簡単に求めることができた1問です。確実に正解しなければなりません。

(2)

下の図のようにアとイに分けて考えます。

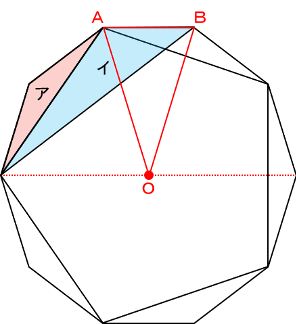
アは正十角形から正五角形を引いた面積を5等分すれば求まります。
イをどのように求めればよいのかで悩んだ受験生もいたことでしょう。
イは等積変形をすれば図の赤い三角形OABと同じなので、正十角形の面積の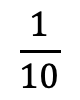とわかります。この等積変形に気付けるかどうかがポイントでした。

４

(1)

分母が72で1より小さい既約分数が何個あるのかを考える問題です。
ほとんどの受験生が解いたことがあると思われる典型題でしたので、しっかりと正解したいところです。

(2)

求め方の手順はいくつか考えられますが、420グループの分母は421なので、1から421の中に3の倍数でないものが何個あるのかを考えるのが最も自然でしょう。
421÷3＝140あまり1　より、140個あることがわかりますので
421－140＝281（個）
という答えにしてしまいそうですが、ここで「分母が1，2の場合は分子が3の分数がもともと存在していない」ことに注意しなければいけません。
よって、281－2＝279（個）　が答えとなります。
決して難しい問題ではないものの、よく注意していかないと最後の正解まではたどり着けなかったことでしょう。

(3)

受験生の誰もが解いたことのある「積が5で何回割り切れるか」という問題でした。
20グループから30グループまでのすべての分数の分子を素因数分解したときに、「×5」が何個登場するのかを考えればよい問題です。
グループごとで、素因数（素因数分解した際に出てくる1つ1つの数）に「×5」を持つ分子だけ調べていきましょう。
たとえば、20グループの場合、分母が21ですから、5，10，15，20の4つの数が素因数に「×5」を持っていますが、15はそもそも分母が21だと既約分数ではなく約分できてしまうため実際には存在しません。このようなことに気をつけながら正確に調べていきましょう。

合否を分けた一題

難易度はそれほど高くないのですが、最後の問題であるため、時間もそれほど残されていない状況であったと思われます。その中で正確に状況整理をしながら煩雑な計算処理もこなさなければならない問題でした。問題を解くうえで、いかに冷静に必要な部分だけをとらえるかが合否を分ける鍵となります。

(1)

令子さんが「AからBへ向かう途中で1度だけバスに抜かれる」ということから、もちろんそれは9時7分発のバスであることがわかります。
9時7分のとき、令子さんはAから12×＝1.4 (㎞)進んでいますから、そこから
1.4÷(16－12)＝0.35 (時間)　→　21分でバスに追いこされることがわかります。
つまり、令子さんがＢ地点に着いたのは9時から7分＋21分＋3分＝31分
経ったときですから、AからBまでは、12×＝6.2 (㎞)と求まり

(2)

まずは問題文にある「令子さんがAを出発してからCを出発するまで」の時間を求めましょう。令子さんはAからCまでを途中休まなければ
(23.2－7.6)÷12＝1.3 (時間)　→　78分かかりますので、
実際には9時から、78＋5＋11＝94 (分後)にCを出発したことになります。
この94分の間に何本のバスがCに到着するのかを考えましょう。
9時にAを出発した1本目のバスがCに到着する時刻は、9時から
(23.2－7.6)÷16＝ (時間)　→　58.5分
58.5＋1＝59.5 (分後)
と求められ、その後は7分おきにバスがCに到着することがわかります。
よって、求める答えは、(94－59.5)÷7＝4あまり6.5より4＋1＝5 (本)となります。

(3)

(2)より、令子さんは9時から94分後にC地点を出発していることがわかっていますので、まず、9時にAを出発したバスがDを出発したのが9時から何分後なのかを考えます。
バスはAからDまで停車時間を考えなければ、23.2÷16＝1.45 (時間)　→　87分
かかりますので、Ｄを出発するのは9時から、87＋1×2＋10＝99 (分後)とわかります。
よって、バスがＤを出発したときにバスと令子さんの間の距離が
と求められ、この　→　にすれちがいます。
これは9時からですので、
＝10時56分20秒と答えが求まります。

雙葉中の算数は、基本的な典型題が多く出題されますが、この速さの問題や図形の問題のように、しっかり計算していくことと丁寧に問題文を読み解くことが求められるものも毎年出題されます。ここで焦ってしまうと、時間が足りなくなったり、解けるはずの典型題でもミスをしたりしてしまいます。普段の学習から、落ち着いて問題文をよみ、丁寧に式を書き、正確に計算することを心がけましょう。

著者：江田勝

この記事は役にたちましたか？