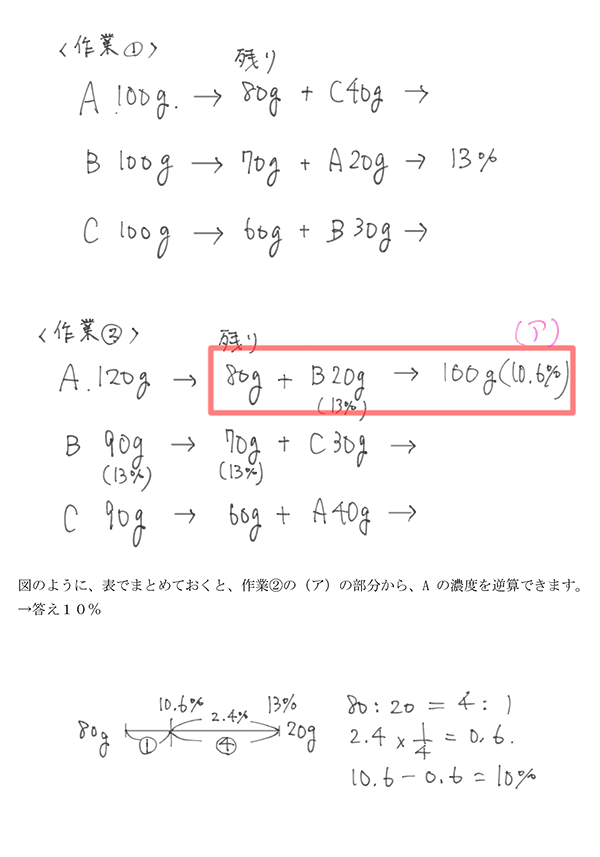算数の合否を分けた一題（2019年度）

算数の合否を分けた一題

雙葉中入試対策・算数の合否を分けた一題（2019年度）

難易度分類

［１］	（１）A　（２）A　（３）A
［２］	（１）A　（２）B
［３］	（１）A　（２）A　（３）A
［４］	（１）A　（２）A　（３）B
［５］	（１）A　（２）B　（３）B

Ａ：雙葉中合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、一旦とばすべき問題

問題別寸評

「難しい年の次は簡単になる」とよく言われますが、今年の雙葉中の問題は、かなり解きやすい問題だったと言えるでしょう。
ただ、解きやすくはあるものの、中盤の［３］では気を抜くと失点してしまいそうな、こまかな注意ポイントが隠されていました。また［４］は基本的な問題ではありますが、雙葉らしい複雑な数値処理を伴う問題で、ここも気を抜くことはできません。
［１］～［４］でとりたてて難しいという問題はなかったので、差が付いたのは［５］だった思います。今回は、この［５］が合否を分けた１題になった可能性が高いと思いますので、後ほどとりあげて解説したいと思います。

［１］

（１）
あまり工夫するところもない普通の計算です。ここはしっかり得点しましょう。

（２）割る数も割られる数もわからないという問題ですが、ごくごく基本的な典型題に属する問題です。差の公約数に注目しましょう。

［２］

正三角形は高さをおよその値でしか求められません。（中学で√を習ってから正確な求積ができるようになります）この事を理解していれば、図形全体の面積が179.04㎠というのは、正三角形の高さを逆算させるためにあるということがわかります。
（１）で正三角形の面積を求めるので、それを利用して（２）も解くことができます。

［３］

循環小数の規則性を利用したごく基本的な問題ですが、（３）で2019番目の1という問題で、最初の1が整数の1の位にあるということに気を付けなければいけません。
普通の循環小数の問題でよくある、小数第一位からの繰り返しだけしか見ていないと間違ってしまいます。注意力の試される問題でした。

［4］

（１）AとBの面積比が３．１４：４です。収穫量はどちらも同じなので、この比を用いて計算すれば、５×３．１４÷４＝３．９２５ｋｇがBの単位あたりの収穫量とわかります。
（２）Aの単位あたりの収穫量を①とおき、Bの単位あたりの収穫量を①＋1.71とします。
これに、面積比の3．14と4をかけたものが、総収穫量であり、その比が1：2となります。
これによって①を求める事が出来ます。

合否を分けた一題

［5］
3つの容器A、B、Cに濃度の異なる食塩水が100ｇずつ入っています。これらの食塩水に作業①をしました。
＜作業①＞　Aから20ｇ、Bから30ｇ、Cから40ｇ取り出す。つぎにAから取り出したものをBに、Bから取り出したものをCに、Cから取り出したものをAに入れて、それぞれよくかき混ぜる

作業①のあとのBの濃度は13％でした。作業①で出来た食塩水に作業②をします。

＜作業②＞　Aから40ｇ、Bから20ｇ、Cから30ｇ取り出す。次にAから取り出したものをCに、Bから取り出したものをAに、Cから取り出したものをBに入れて、それぞれ良くかき混ぜる

作業②の後のAの濃度は10.6％でした。
（１）作業①のあとのAの濃度を求めなさい。

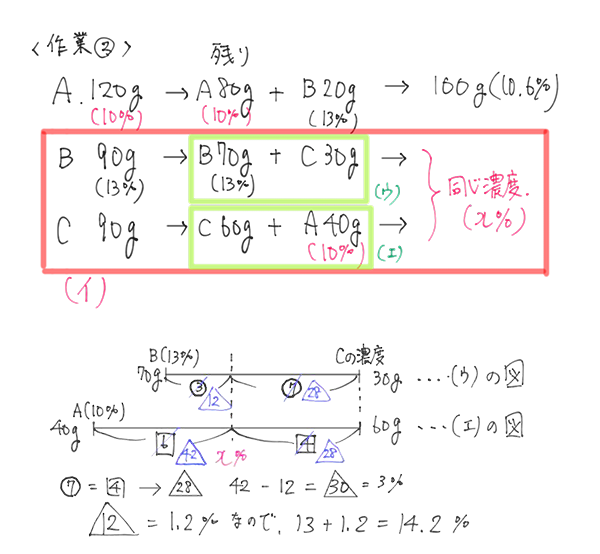
（２）作業②の後、BとCの濃度が等しくなりました。このとき、B、Cの濃度は何％ですか。ただし、作業①の後のCの濃度は、A、Bの濃度より高くなっていました。

ポイントは濃度線分図を上下にキッチリと重ねて書くことで、△、○、□の比合わせを上手に行うところです。天秤の図を書いてしまうと、ごちゃごちゃとしてかなり解きづらくなってしまうと思います。上図のようなシンプルな書き方ができるかが重要です。

（３）最初Cの濃度はAの濃度の３倍でした。最初のA、B、Cの濃度はそれぞれ何％でしたか。

（２）が解けてしまえば、最後は簡単です。
最初のAとCの混ぜ合わせ操作（オ）から、濃度を逆算できます。
これより、Aの濃度が6％とわかりますので、Cはその3倍の18％、
またBは、A（6％）とBを20ｇ：70ｇで混ぜて13％になったということから逆算し、15％と求める事が出来ます。