算数の合否を分けた一題（2018年度）

算数の合否を分けた一題

雙葉中入試対策・算数の合否を分けた一題（2018年度）

難易度分類

［１］	（１）A　（２）A　（３）A
［２］	（１）A　（２）B
［３］	A
［４］	（１）A　（２）B　（３）C
［５］	（１）A　（２）B　（３）C

Ａ：雙葉中合格を目指すなら必ず得点したい問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して、一旦とばすべき問題

問題別寸評

ここ数年続いていた易化傾向に歯止めがかかった印象です。
大問［１］〜［３］は、スムーズに解ける問題が多いですが、雙葉中では非常に珍しい出題となる［４］の時計算、そしてここ１０年以上出題されていない、正四面体型のサイコロの問題［５］という特異な組み合わせに戸惑った受験生も多かったのではないでしょうか。
また、［２］の年齢算は難易度こそ高くありませんが、雙葉らしい注意力と緻密さを要求する問題で、この［２］をしっかり取れたかどうかも合否を左右している可能性が高いと思われます。
時間配分としては［３］までをどれぐらいスムーズに進められたかと、その後につづく［４］と［５］において難度の判断をしっかりと行い、部分点を含めて（１）、（２）をどれだけ取れたかどうかが合否の分かれ道と言えそうです。

［１］

（１）

等差数列の和の公式で処理　→　ア＝（１＋７７）✕７７÷２＝３００３
３００３-２７６３＝２４０ですが、連続する３つの数の和＝２４０としてはいけません。
例えば１、２、３を「―」に変えると和が１２少なくなります。つまり、３つ連続した数の和は１２０ですので、１２０÷３＝４０（真ん中）、その前後なのでイ〜エは３９，４０，４１となります

（２）

最小公倍数の問題です。４０、１５、６の最小公倍数は１２０なので、積み上げる個数は、３個、８個、２０個です。したがってレンガの個数は３✕８✕２０＝４８０個

（３）

どのテキストにも載っている基本問題です。
（２２５＋４５０）÷０．０５＝１３５００、１３５００✕０．８５―２２５＝１１２５０円

［２］

（１）

手がかりになるのは現在の「兄が２０歳未満」「妹は兄の半分」という記述です。
このことから、兄は偶数で、１８、１６、１４、…　妹はその半分の９、８、７、…　と言えますので
現在の兄、妹、私の年齢の合計は、１８＋９＋１２＝３９、１６＋８＋１２＝３６、１４＋７＋１２＝３３…となります。従って２年前は、さらにこれらを６引けばよいので、３３、３０、２７…です。
祖母の年齢は、これを３で割った値（平均）の６倍なので、２倍して求めます。
よって、祖母の２年前の年齢は６６、６０、５４…となり、現在の年齢が６８、６２、５６…です。
問題条件により祖母は現在６０以上なので、６８と６２のみがあてはまります。
よって答えは６８歳と６２歳です。

（２）

（１）の結果を受けて、　
祖母の年齢が６８歳　→　現在の兄、妹、私の和＝１８＋９＋１２＝３９
祖母の年齢が６２歳　→　現在の兄、妹、私の和＝１６＋８＋１２＝３６
よって、２年後の子供たちの和はこれに６を加えた４５歳、４２歳のどちらかです。
４５歳のとき　：　父＋母＝４５✕２＝９０　父＝（９０-４）÷２＝４３歳（２年後）　→　４１歳（現在）
４２歳のとき　：　父＋母＝４２✕２＝８４　父＝（８４-４）÷２＝４０歳（２年後）　→　３８歳（現在）
問題文の条件により、父は現在４０歳以上なので、答えは父が４１歳、母が４５歳です。
（母が「年上」という条件に気を付けて下さい・・・）

［３］

図のように補助線を引くことが出来れば
簡単な問題です。

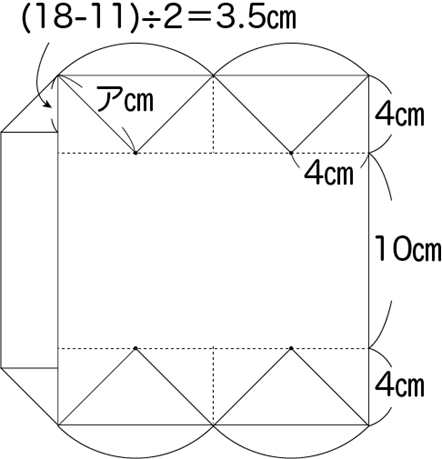
一辺４㎝の直角二等辺三角形が８個、
半径ア㎝、中心角９０°のおうぎ形が４つ
横１６㎝、縦１０㎝の長方形
上底１１㎝、下底１８㎝、高さ3.5㎝の台形
で構成された図形と分かります。
半径アが分からないのは、雙葉受験生なら
お馴染みの方法で処理出来ることには
すぐ気づきたいところです。
（ア✕ア＝4✕4✕2＝32）
4✕4÷2✕8＋32✕3.14＋（18＋11）✕3.5÷2＋10✕16
＝375.23㎠

［4］

次ページで合否を分けた一題として扱います。

［5］

１０年前まで遡っても雙葉中の問題で、立体の展開図が出されたことは記憶にありません。今回の出題は受験生には相当のサプライズだったのではないでしょうか。
しかしながら、（１）は三角すいの展開図を一度でも解いたことのある受験生ならばさほど苦労せずに正解できたと思います。
ポイントは（２）を数の並べ替えの問題に落とし込めたかどうか・・・というところでしょう。

（１）

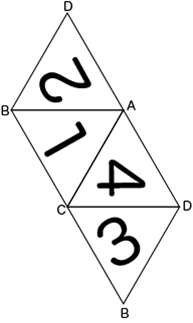
頂点に記号をふり、文字のあたまや底辺がどの頂点を向いているかを一つ一つ確認しながら進めましょう。文字のように下線を引いておくと対応関係が見やすくなります。

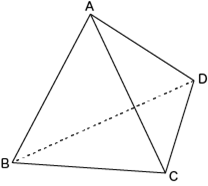
（２）

三角すいのサイコロは、図のようにまとまった４つのマスの中に、すべての数字が入ります。

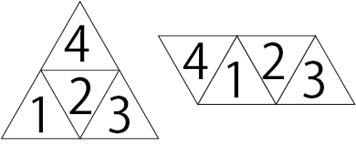
したがって、このような図を書いて調べると分かりますが、結局は４が下に置いてある状態からは、最初に１へ転がせば、その次の移動は２，３，４のどれか、
２を選べばその次は１，３，４というように、数字を連続させずに、合計を６にするという和分解のタイプの問題に落とし込むことが出来ます。

３回で６にするので、１＋２＋３と、１＋４＋１のタイプに分けられるので、
答えは、１→２→３、１→２→３、２→１→３、２→３→１、３→１→２、３→２→１
１→４→１の７通りです。

（３）

５回で和を13にします。また、前問と同様、同じ数が連続してはいけません。
4の回数で分類します。

3回：
4、〇、4、〇、4　という置き方しか出来ませんが、スタートの目が4なので、4を最初に持ってくることが出来ませんし、合計を13にすることもできません。したがってこれは不可能です。

2回：（残り3つで5 →3，1，1か2、2、1）
ア　〇、4、〇、4、〇　→　3，1，1で3通り、2，2，1で3通り
イ　〇、4、〇、〇、4　→　3，1，1で2通り、2，2，1で2通り
ウ　〇、〇、4、〇、4　→　3，1，1で2通り、2、2，1で2通り
7+7＝14通り

1回：（残り4つで9→ 3，3，2，1か3，2、2、2）
ア　〇、4、〇、〇、〇　→　3，3，2，1で8通り、3，2，2，2で1通り
イ　〇、〇、4、〇、〇　→　3，3，2，1で8通り、3，2，2，2で0通り
ウ　〇、〇、〇、4、〇　→　3，3，2，1で8通り、3，2，2，2で1通り
エ　〇、〇、〇、〇、4　→　3，3，2，1で6通り、3，2，2，2で0通り
8✕3＋6+2＝32通り

0回：（3，3，3，2，2）
3、〇、3、〇、3の1通りのみ

以上より、14＋32＋1＝47通り

合否を分けた一題

今年は例年の出題傾向を裏切るような問題が多かったため、これまでの出題傾向に拘ることなく、様々な問題をまんべんなく練習していた受験生が有利だったと言えます。
そのなかでも、「時計が途中から逆回転をする」というちょっと変わった設定の時計算である［４］を合否を分けた一題として取り上げたいと思います。
（１）は難易度としては高くはないものの、常に逆回転するのではなく、３時20分から逆回転ということがどういう意味を持つのか。池の周りを回る旅人算などを通して時計算の本質をきちんと理解していたかどうかが問われていたと言えるでしょう。
（２）からは煩雑な数値計算の連続で、途中で音を上げた受験生も多かったでしょう。
効率的な処理が成否を分けたでしょう。ややこしい条件をできるだけ簡素にまとめなおすスキルと、効率的な計算処理方法の両方が必要であり、非常に難度の高い問題と言えます。
（３）は時間制限を考えると、正解に至るのは至難の業と言えます。これは解説のような効率的な計算方法が見えないなかで取り組むべき問題とは言えません。
（２）を正解できればかなりのアドバンテージが得られたと思います。

（１）

３時２０分までは時計回り、その後折り返してくるので、
図のような短針と長針の出会い算として処理。

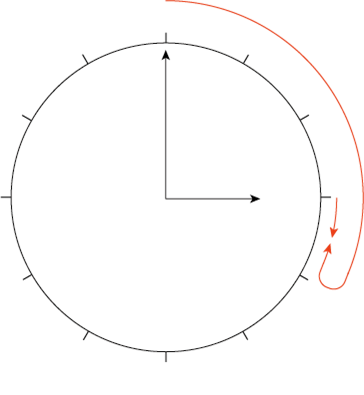
（30＋120）÷（0.5＋6）＝分
→3時分

（２）

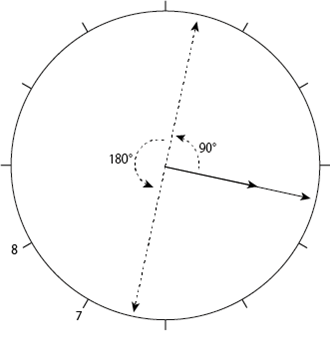
3時分から長針が短針に対して逆向きに90°
動くので、３時をスタートとすると、150＋90＝240°の
出会い算とすることが出来ます。
その後、さらに180°動くごとに短針との角は90°
となるので、その時刻を羅列していきます。
240÷6.5＝480/13分
（240＋180）÷6.5＝840/13分
（420＋180）÷6.5＝1200/13分…
という規則性のある数字が並びます。
３時→７時までは４時間＝240分＝3120/13分
８時までは５時間＝300分＝3900/13分
なので、この数列が3120/13〜3900/13の間にある時刻を
求めます。
（3120-480）÷360＝７あまり120より、480＋360✕8＝3360
よって、3時から3360/13分後＝分後＝4時間分後→ 7時分
もう一つが、その360/13＝分後の、7時分

（３）

題意の時刻は、10時を過ぎていますので、10時ちょうどにおける短針と長針の位置をそれぞれ考えておきます。
短針 → 10の文字の位置です
長針 → 10時〜3時は7時間＝420分あり、そのうち20分間は時計回り、400分間は反時計回りをしたので、12の文字から6✕（400-20）＝2280°反時計回り
2280÷360＝6あまり120°なので、長針の位置は、8の文字のところです。

ここで、長針と短針のちょうど中間を動く、第三の針を考えます。
この針は、（6-0.5）÷2＝2.75°ずつ反時計回りに動く針です。この針が4の文字、または10の文字に来た時、直線アによって、短針と長針のなす角が2等分されます。
10時ちょうどにおいて、この針は9の文字にあり、反時計回りなので、先に4の文字に来ますので、その時刻は、150°÷2.75＝分です。　→10時分