算数の合否を分けた一題（2015年度）

算数の合否を分けた一題

雙葉中入試対策・算数の合否を分けた一題（2015年度）

難易度分類

大問１	（1）Ａ　　（2）Ａ　　（3）Ａ　　（4）Ａ
大問２	（1）Ａ　　（2）Ａ
大問３	（1）Ａ　　（2）Ｂ
大問４	（1）Ａ　　（2）B　　（3）B
大問５	（1）Ｂ　　（2）Ｃ

Ａ：雙葉中学を目指すなら落とすことの出来ない問題
Ｂ：着眼点や解法ツールにより正答率・かかる時間に差がつく問題
Ｃ：難易度や処理量から判断して５分以内に解き切る腕力がなければ後に回すべき問題

問題別寸評

［１］計算＋小問集合

極めて易しい出題です。
(１)分数よりも小数で計算した方が速いという判断が欲しいところ。20.15という数値にニヤリとした受験生が多かったのではないでしょうか。

(２)5年生基礎レベルの相当算。絶対に落とせません。

(３)流水算と比です。「上りにかかる時間は下りにかかる時間の1.6倍」という条件を見た瞬間に
上りと下りの速さの比が5：8、静水：流速は6.5：1.5とスムーズに計算しましょう。

(４)売買損益の基本問題。1/7は68円、6/7は112円で売ったことになります。
途中数値が分数での計算が続きますが、落ち着いて計算です。

［２］図形の移動

(１)正三角形の移動の定番。難しいところは一切ありません。
(２)作図さえ完成すれば、②も楽勝です。
正三角形が転がる際、回転の中心に対して２パターンの位置関係があることのみ注意。
いい加減に捉えていると、ミスに繋がります。

［３］旅人算

(１)速さを求めるだけの計算問題。
(２)弟を兄が追い越すのは、弟が休んでいる7分間のどこかです。
最初の一回を求めると、弟は休憩をはじめて5.5分後に追い抜かれています。
兄と弟の出発時刻は1.5分ずつずれてゆきますから、兄が弟を追い越すのは休憩時間の
5.5分⇒4分⇒2.5分⇒1分後と次第に短くなり、これ以降は追い越すことができません。
弟が4回目に休憩したときの距離を求めればOKです。

［４］

合否を分けた1題として後述します。

［５］水槽の問題

(１)は3分以内、(２)はパッと道筋が見えなければ捨て問という判断で良いでしょう。
(１)容器に水は侵入せず、ただのおもりと考えてしまってＯＫです。
底面積が18ｃｍと27cmの正方形ですから、2：3と簡単な比に直し
容器と水そうの底面積比が4：9。
容器を入れる前9だった底面積が入れた後9－4＝5に変化しているため
水の高さは逆比で5：9で変化したと解ります。
14.4×5/9＝8cmですね。

(２)水の深さの9cmが容器の丁度半分であることに気づけるかがポイントです。
容器を完全に水没させるには、丁度2倍の27×27×8×2㎤の水量が必要です。
27×27×18－27×27×16＝27×27×2㎤が容器の枠組みの体積です。
18×18×20－27×27×2＝5022㎤が容器の容積となります。

合否を分けた一題

今年も雙葉らしい「丁寧に、素早く調べ上げる力」が問われる出題でした。ひっかけを伴う意地の悪い問題が影を潜め、スピードの勝負になった可能性があります。特に［４］の日暦算は調べ方によって大きく時間に差がつく問題でした。着想のまま何も考えず調べるのではなく、どのように整理すれば最も効率的に調べられるかベストな方法を模索する能力が合否を分けます。

［５］日暦算

（１）とりあえず書き出しましょう。書き出しながらどのようなルールがあるかを考えます。
2015日⇒16月⇒17水⇒18木⇒19金⇒20土⇒21月⇒22火⇒23水⇒24木⇒25土⇒26日
うるう年の次の年度に曜日が2つ先に進むことがわかります。

(２)これもただひたすら書き出しても良いですが、ルールをみつけておくと(３)が楽です。
曜日別に表を作り、閏年の影響でどの曜日が飛ばされるのか、いくつで周期をするのかを考えつつ書き出してみましょう。

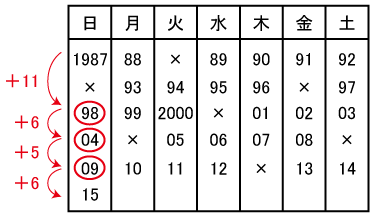
書き出しにより、1998、2004、2009となります。

(３)
4年に一回閏年で曜日が2つ進むので、曜日の変化は「4つ進んで1つ飛ばす」という5年の周期で進んで行きます。一週間の周期と組み合わせると、35曜日で周期します。1つ飛ばして進むので、年度としては35曜日から、閏年によって飛ばされる7曜日を引いた28年ごとに同じ曜日に戻ることがわかります。
(２)の1987～2014は丁度28年の周期１つぶんにあたるので、
2015年から同じ繰り返しです。

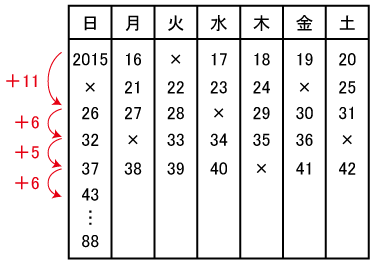
日曜日は＋11、＋6、＋5、＋6年ごとに進みます。
2015、2026、2032、2037・・・と書き出してゆくと、10回目は2088年となります。