算数の合否を分けた一題
フェリス女子中入試対策・算数の合否を分けた一題（2016年度）
難易度分類
| １ | （１） A （２） A （３）① B ② B （４） ① B ② B （５） ① A ② A |
|---|---|
| ２ | （１） B （２） B （３） B |
| ３ | （１） A （２） A （３） A （４） B |
| ４ | （１） A （２） C （３） B |
| ５ | （１） B （２） C （３） C |
A…フェリス女学院中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点に大きく差がつく問題
C…難度、処理量から判断して、部分点を拾えればよしとする問題
出題総評
例年通りのセット。問題順と難度があまり関係ないのがフェリスの特徴の一つです。1問1問1番から確実に決めようとすると大きく時間ロスしかねませんので、前半の小問でも、重いものは思い切って飛ばして、易しいものから確実に決めていく戦略が必要です。
図形では立体と、円に関する角度・面積が多く出題されます。中心角と円周角の関係等、踏み込んだ学習をしておけば有利に働くでしょう。
今年の算数は受験者平均が100点満点中50点でした。算数の出来具合によって、かなり大きな得点の開きがあると思われます。理科は受験者平均で44点／60点と高水準となってしまったので、理科で差をつけることは難しかったでしょう。1題1題の難度を考えると、処理の手際の良し悪しで差がついていると考えられます。
問題別寸評
（１）
基本的な計算問題です。
（２）
円がらみの角度。半径2本→二等辺三角形 を押さえていくと、答えにたどり着きます。
（３）
平均の速さ。
「往復の平均の速さ」は「行きの速さと帰りの速さの平均」で求めることが出来ません。理由は、行きと帰りの時間が異なるからです。本題については後述します。
（４）
推理の問題です。表に起こし、不確定部分は場合分けして処理しましょう。
（５）
円と角度の問題。フェリスに合わせてトレーニングしていれば、かなり易しい部類。
弧の長さが2：3なので、中心角150°を2：3に配分します。
底角15°の二等辺三角形は、瞬時に求まるはず。
問題自体は重くないのですが、処理速度の差が付きそうな問題です。
（１）
1日目の入場者：2日目の入場者＝2日目の入場者：3日目の入場者なので、
1.44＝1.2×1.2から、総入場者数を1：1.2：1.44に配分し、3日目の1.44が180人であることを用いて総人数を求めます。
（２）
人数比 1.2：1.44
時間比 1：1.5
の商を取って時間当たり人数の比求めます。
（３）
人数比 1：1.2
時間当たり人数比 10： 9
の商を取って、時間比が求まります。
（１）
重なりの図形をイメージする問題です。
（２）
面積＝6㎠となる時刻をすべて求めます。台形の両端から、6㎠を切り取るラインを決めるのが比較的やさしい図形なので、容易に求められるでしょう。
（３）
ＣＤの中点と、長方形の対角線の交点との出会い、と方針が立てばすぐ終わるでしょう。
（４）
すべての場合を答えよ、とあります。1：2の取り方は、Ｂが長方形の外部にあるときと内部にある時の２通り存在します。ちなみに、Ｃが長方形の外側（右側）に出てしまうと、
1：2になる位置が存在しません。
（１）
四角すいの公式通りでもよいですが、立方体が四角すい６個を合わせたものであることを考えて、立方体×1/6 で求めるのが良いでしょう。
（２）
何通りあるか、と聞かれているので、膨らんでいるのか、へこんでいるのかの２通りがあるのだということに自然に気づくでしょう。展開図には頂点が書かれていないので、上下は考えず、凹凸のパターンのみで判断する必要があります。
（３）
四角すい２個分をくり抜いた立体となりますから、（１）と同様に考えて、立方体×4/6で決まります。
問題の意味を取るのがかなり大変な問題。（１）こそ誘導になっていますが、状況を的確に把握しないと（２）には進めないでしょう。問題順を考えても、（２）以降は白紙、という受験生が多かったと推測され、合否を分けるような差はつかなかったと言えるでしょう。
（１）
男女とも、ＡグループとBグループの人数が等しいと仮定すると、男子平均＝55、女子平均＝50となってしまいます。ここから、男子はＢグループの方が7人多く、女子はAグループの方が7人多くなることで、平均点が逆転するのだな、と確認するためのヒント、誘導となる設問になっています。
（２）それぞれの人数を
A B
男子 ① １+７
女子 ①+７ １ として考えます。
男子の平均点は、40 + 30×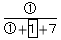 
女子の平均点は65－30× 
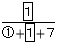となるので、
２つの平均点が逆転する条件は
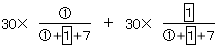が25点を上回る、すなわち
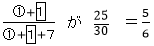を上回る、すなわち
①+１が35を下回る、ということになり、これと①、１がともに1以上であることを合わせて、アは34×2 + 7×2 ＝82、イは4 + 7×2 ＝18となります。
（３）
平均点を低くするためには、①+１+７＝30人の内訳について、１をできるだけ大きくとることを考えればよく、①＝１、１＝22として、全体平均を求めます。（２）をクリアしている受験生にとってはボーナス問題と言えるでしょう。
合否を分けた一題
問題による難度の差が大きいので、難度の見極めが重要です。標準的な問題であっても、自分なりに速く処理する方法を日々の学習の中で身につけることが見えない差となります。
そのような意味で今年の合否を分けた１題として、１（３）を取り上げます。「平均の速さ」に翻弄されずにスピーディーに処理できた受験生は確実に時間差＝得点差をつけることが出来たでしょう。
①行きの速さは2日とも等しいとわかっているので、時間は1：1となります。帰りの時間は速さの逆比で表して、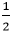
と 
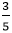が求まります。
これは合計時間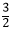 
と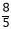 
を求めるための誘導となっており、この合計時間の逆比が「往復の平均の速さ」の比となりますから、
：
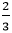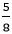＝16：15
この差1が0.3㎞／時にあたるので、1日目の往復の平均の速さは、16 ＝ 4.8㎞／時。
一方、
1日目行き 1日目の往復
距離 1 ： 2
時間 1 ：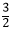
速さ 3 ： 4
ですから、１日目の行きの速さは
4.8×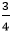
＝3.6 ㎞／時となります。
平均の速さについては、「速さの平均にはならない」ことは経験的にわかっていても、その理由まで考えるチャンスはあまりないのではないでしょうか。
たとえば、かかった時間の比を考えて加重平均をとることによって平均の速さは求められます。そのくらいの腕力があれば、あえて誘導に乗るよりも速く楽に答えが出せる場面が多くなるかも知れませんね。
(2 votes, average: 3.50 out of 5)
Loading ...
フェリス女子中入試対策・関連記事一覧
フェリス女子中入試対策・同じ教科（算数）の記事
フェリス女子中入試対策・同じテーマ（合否を分けた一題）の記事
他校の同じ教科（算数）の記事
