算数の合格戦略の提案

算数

麻布中入試対策・算数の合格戦略の提案（3ページ目）

４．問題の(2)のヒントは(1)にある！

麻布中の問題は、その順番が良く考えられており、実は解き易く、
よく考えられた構成になっています。例えば、問題に(1)、(2)があったとしましょう。

(1)は比較的簡単に解けます。しかし、(2)は飛躍的に難しくなっています、
いや、そう見えます（笑）。お手上げの生徒も多いでしょう。しかし、よく見て下さい。
(1)は(2)を解くための大きなヒントになっていることが多いのです。

実際に問題を解きながら実例を見てみましょう。

【2008年　問題６】

円の1/4の部分の図形ＯＡＢがあります。次の問いに答えなさい。

(1)右の図において、斜線部分の面積と図形Ｏ
ＡＢの面積の比を求めなさい。ただし、直線OA、CD、EFは平行です。

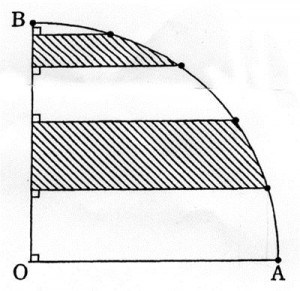
(2)右の図のように図形ＯＡＢの弧ＡＢ(曲線の部分)を５等分した各点からＯＡに
平行な直線を引きました。ＯＡを５ｃｍとしたとき、２つの斜線部分の面積の和を求めなさい。

【解答・解説】

(1)は△EFOと△CODが合同であることに気づくことが重要です。
これが２番で書いた“基礎力”です。

○扇形や円の面積を求める問題は、同じ面積である図形を探しておきかえる
○斜線部分の図形を一部でも含む図形に注目し、合同や等積変形による同じ
面積の図形を探す。
○直角三角形の合同条件が当てはまる図形を探す
○CDとOAは平行、よって角AODの錯角である角CDOは25°

これらは問題集やテキストでよく出てきますが、実践で使いこなすことは中々難しいです。
「この図形とこの図形が合同になる」と覚えるとか、「この２つが合同そうだ」と
言った勘で解いていると麻布中学の問題は解けません。

どことどこの辺の長さ、角度が同じ、それを合同条件と照合し、
どの図形とどの図形が合同であるかを見つけ出すこと

これが“基礎力”なのです。

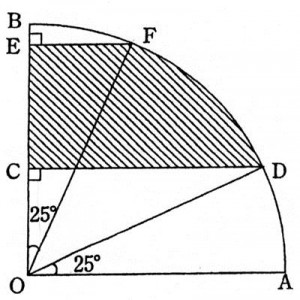
△EFOと△CODが合同ですから、OFとCDの交点をＧとすると、□CGFEと△DGOの面積は同じです。よって求める面積は扇形ODFになるわけです。

よって、斜線部分の面積と図形ＯＡＢの面積の比は中心角の比に等しく、４：９　になります。

答　４：９

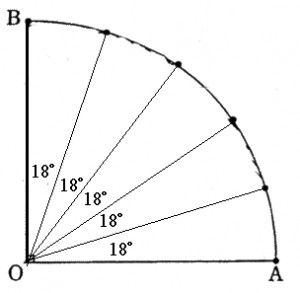
(2)は(1)を使います。弧を５等分ですから、分けられた扇形の中心角も５等分となり、18°になります(右の図)。

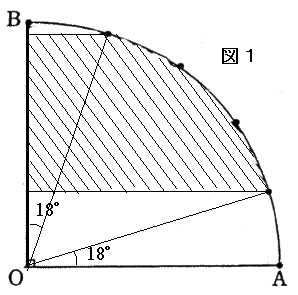
では、例えば、図１の斜線の部分の面積を求める場合、どのようにしたらいいでしょうか。
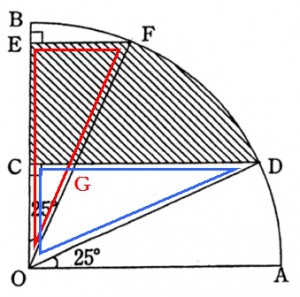
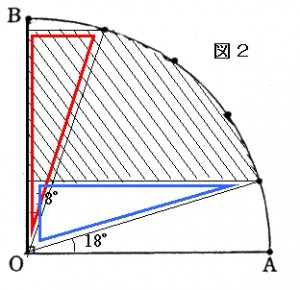
このとき(1)を使います。図２の赤と青の直角三角形は
(1)同様合同ですので、斜線部分の面積は中心角18×３＝54°の扇形になります。

もうお分かりかと思いますが、求める図形の面積は、
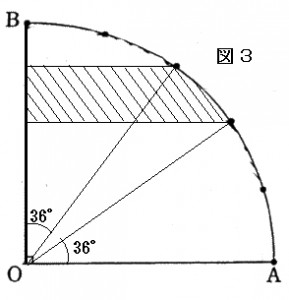
図１の斜線部分－図３の斜線部分になります。
図３の斜線部分も図１の斜線部分の面積同様、
中心角18°の扇形です。

よって、求める面積は
５×５×3.14×(54－18)／360＝7.85

答　7.85　c㎡

麻布中の問題は、このような問題構成になってることが多いのです。
「(2)は(1)を使って解くことが多い」と教えている講師は多いと思いますが、
生徒さんはあまり、これを実行していないようです。

どうしても(2)を解くことに意識が集中してしまって、(1)が見えなくなってしまいます。
(1)と(2)を見比べてみましょう。(1)が当てはまるところがきっと見つかるはずです。

このように何か情報を与えられて、それを使って解く、これが、何度も申し上げてる通り、
“基礎力”です。麻布中学が大好きな出題パターンです。

どんな入試問題でも同様ですが、麻布中の場合は(1)と(2)の問題に
関連がないように見える場合が多く、この法則を忘れてしまいがちです。
是非、この方法を身につけてください。

『算数の合格戦略の提案』 >> 1 2 3 4

著者：受験Dr. (受験ドクター)

この記事は役にたちましたか？

(6 投票, 平均値/最大値: 4.33 / 5)

Loading ...

« 算数の出題傾向分析

算数担当講師から麻布中学入学を目指す皆さんへアドバイス »

麻布中合格対策ドクターのトップに戻る ≫

この記事が気に入ったら是非ご登録を

麻布中入試対策・関連記事一覧

麻布中入試対策・同じ教科（算数）の記事

麻布中入試対策・同じテーマ（合格戦略の提案）の記事

他校の同じ教科（算数）の記事

著者