算数
浅野中入試対策・算数の合格戦略の提案
1）速く正確に解く力
先にも述べたように、高得点勝負となるところで勝ちを収めるためには、まず皆ができる問題を落とさないということである。それでは、「皆ができる問題」というのはどういうものなのか、特に□2の一行題形式で頻出単元は抑えておくこと。数の性質、特殊算（つるかめ、消去、過不足、差集め）、時計算、平面図形、回転体の体積・表面積など。そしてその□2は（１）～（６）のだいたい6問で構成されているが、その6問を5，6分以下で解けるのが理想であろう。
対策としては、入試問題がたくさん集まっている日能研から出版されている「銀本」の過去問から1行題のところをひたすら解くという練習が良い。そして、ただ解くのではなく、時間を計ること。いかに速く正確に解けるかということが勝負の分かれ目となってくるので、日ごろから「10分で10題を解く」「15題解くのに何分でできるか計る」など、ある一定時間内にどれだけの問題数をこなせるのか、その力を磨く必要がある。スピーディーに尚且つ正確でなくては得点には結びつかない。
２）計算力をあげる
先にも述べたように、計算力は必須である。ただ、正しい答えを導き出す力だけではなく、工夫や粘りも必要。またＨ２０年は、還元算も出題されている。
Ｈ20年□1（１）
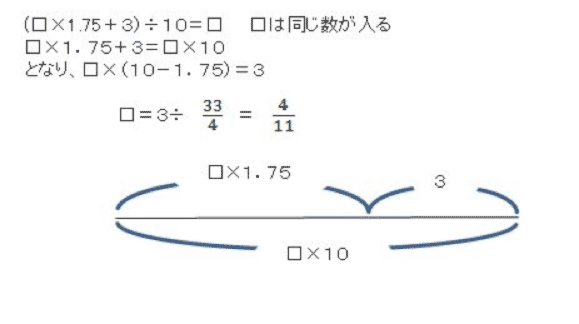
上記のような還元算は、迷ったら線分図を書き□がいくつ分かを考えると良いでしょう。
計算力とは、ただ単に答えがあっていればいいというのではなく、やはり限られた時間内にいかに正確に答えられるかということが求められている。そのためには、筆算に頼らない暗算力と覚えてしまった方がよい数値は覚えてしまい自由自在に使えるようにしておくことが肝心である。
① 筆算に頼らない暗算力
日々の練習量で決まる。指導していて横で見ていて気になるのは、75÷3など簡単なものまで筆算してしまい、途中でどこをやっているのかわからなくなり、写し間違いや書き間違いをして失敗しているということである。丁寧な生徒ほどこの状況に陥ってしまっているのが事実。簡単なものは、答えをぱっと出せる勇気が必要でその勇気は日ごろの練習量で決まると考えている。
② 覚えてしまった方がよい数値
円周率の掛け算、例えば、2×3.14、3×3.14、・・・や、16×3.14 、25×3.14などは覚えてしまいましょう。また、平方数も規則性などでよく出てくるので19×19くらいまでは覚えること。
３）図形・立体問題
平面図形では、基本図形をまず頭にいれておくこと。あくまでも基本図形でよい。
単純に規則性、場合の数が出るのではなくそれと関連させて、図形や立体の中で規則性を見つける問題なども出題されている。そのため、基本的な図形の性質も頭に入れておくこと。また、図形上の点の移動における規則性も浅野は好んで出題するので注意。Ｈ２４年□7を例に挙げると、立方体の辺上を３点が動き、その３点を結んでできた線で立体を切断するという問題が出ている。「点の移動」＋「立体の切断」が絡まっている高度な問題である。ただ、一見難しそうであるが、じっくり読んで（１）、（２）が解ければ（３）は簡単である。
(3 votes, average: 5.00 out of 5)
Loading ...
浅野中入試対策・関連記事一覧
浅野中入試対策・同じ教科（算数）の記事
浅野中入試対策・同じテーマ（合格戦略の提案）の記事
同じテーマの記事はいまのところありません。
※ ただ今、当塾の講師陣が一生懸命執筆しております。
執筆がすみ次第、随時公開いたします。
今しばらくお待ちください。
他校の同じ教科（算数）の記事
