算数の合否を分けた一題
浅野中入試対策・算数の合否を分けた一題(2020年度)
難易度分類
| 1 | (1)A (2)A (3)B (4)B (5)B |
|---|---|
| 2 | (1)A (2)A (3)B (4)B (5)B |
| 3 | (1)A (2)A (3)A (4)B |
| 4 | (1)A (2)A (3)B |
| 5 | (1)A (2)B (3)A (4)B |
A…浅野中合格を目指すなら、確実に得点したい問題
B…解法や着眼点次第では、得点に大きな差がつく問題
C…難易度・処理量などから判断して、差はつかない問題
2020年度 出題総評
全体的に見て、極端に難易度の高い問題はなかったものの、何に注目すればよいのか気づきにくく、アプローチしづらい問題が多かったために、合格者平均得点率は64.2%とさほど伸びませんでした。
また、大問1の(5)に「説明しなさい」という問題がありましたが、ちょっとした誘導があるとはいえ難易度が高いため、時間をかけすぎずに他の問題に時間を充てられたかどうかも受験生にとって大きなポイントだったと思われます。
年度によって難易度(得点率)の上下幅が大きいので、どちらの場合にも冷静に対処できるような訓練・経験を積ませることが非常に大切な学校と言えるでしょう。
問題別寸評
(1)
分数・小数を含んだ一般的な逆算の問題です。確実に得点しましょう。
(2)
仕入れた品物の個数を①として計算式を作って解く問題(マルイチ算)です。
浅野中に合格するためには確実に取りたい問題です。
(3)
動く点が3つありますが、最難関校を目指す受験生であれば身につけているであろう「シャドー」の考え方を用いれば、さほど難しくはない問題です。この考え方が定着されていない受験生にとっては、やりにくい1問だったかも知れません。
(4)
操作A、操作Bの2種類の操作をすることによって、黒玉と白玉の個数がどのように変化していくかをとらえる問題です。
「すべての黒玉をそれぞれ黒玉1個と白玉1個に変える」というのを、「操作前の黒玉と同じ個数だけ白玉が増える(黒玉の個数はそのまま)」ととらえることができれば、それほどやっかいな問題ではありません。
また、それ以外にも、地道に操作Aを続けて3回、その後操作Bを続けて5回、その後操作Aを数回続けたときの黒玉と白玉の個数を調べていくことで、規則性に気付き正解した受験生も多かったと思われます。
(5)
文章や図を用いて、受験生に自由に「説明させる」問題でした。
最終的に説明させたい問題に向けて、誘導となる1問がはじめに用意されてはいるのですが、それをどのように用いて(つなげて)説明すればよいのか、気づきにくい問題でした。
おそらく、学校側が求めている模範解答どおりに答えられている受験生はそう多くないはずです。
ここで時間を使いすぎてしまわないよう、注意が必要でした。
(1)
一筆書きできる図形の、書き方が何通りあるのかを考える問題でした。
書きはじめの場所(始点)と書き終わりの場所(終点)は決まっていて、途中で分かれる場所での書き順(方向)が何通りあるのかを考えていけば、積の法則で簡単に求められる図でしたので、合格者の多くが得点しているであろう1問です。
(2)
色の塗り分け方の問題です。複雑な図ではないため、確実に得点したいところです。
塾によって指導のしかた(考え方の流れ)が異なるテーマですので、自分の塾での考え方をきちんと定着させる必要があります。
(3)
難易度はそれほど高くない典型題の一種ですが、「過去に戻る」点に注意が必要であることと、「ちょうど◯年前」ではなかったので計算処理が多いため、途中でミスをしてしまうケースも多かったと思われます。
(4)
神奈川区のマークに関する平面図形の問題でした。
点対称性に注目し、どの部分が等しい長さなのかをとらえます。
冷静に図を見ることができれば、気づく受験生は多かったはずです。
(5)
(4)の図の面積を求める問題です。
(4)の答えが求まった受験生については確実に得点しなければならない1問です。
一方で、(4)の答えが求まらなかった受験生は、自ずとこの1問も失点しまうため、この2問で大きな差がついてしまった可能性も否めません。
(1)
特にひねりのないニュートン算です。確実に取りたい1問です。
(2)
(1)と同様、確実に取りたい1問でした。
(3)
つるかめ算を用いるニュートン算でした。典型題ですので、浅野中合格のためには落とせない1問でした。
(4)
5分ごとにポンプが1台ずつ追加され、状況が変化していきます。
はじめの5分間はポンプが1台なので、
水そうAの中身は毎分6-4=2(L)ずつ増え
水そうBの中身は毎分4 Lずつ増えていく。
5分後から10分後の5分間はポンプが2台なので、
水そうAの中身は毎分4×2-6=2(L)ずつ減り
水そうBの中身は毎分4×2=8(L)ずつ増えていく
という状況ですので、水を抜き始めてから10分後に
水そうAには
120-2×5+2×5=120(L)
水そうBには
4×5+8×5=60(L)
入っていることがわかります。
この後の5分間はポンプが3台になるので、
水そうAの中身は毎分4×3-6=6(L)ずつ減り
水そうBの中身は毎分4×3=12(L)ずつ増えていく
ことになります。
よって、このあと

それぞれの時間帯の状況を落ち着いて整理できれば、答えまでたどり着けたことでしょう。
(1)

(2)

この問題も得点したい問題でした。
(3)
ひもをつないでいる点Pが辺上を動くため少し厄介かも知れませんが、浅野中合格者層にとってはイメージしやすかったのではないでしょうか。

を組み合わせた立体となります。
こちらも、合格を確実とするためには得点したい1問です。
合否を分けた一題
極端に難しいわけではないのですが、最後の大問ということで時間もそれほど残されていない状況の中で、正確に状況整理をしながら丁寧に調べていく必要がある問題でした。
また、中でも(1)や(3)については、問われていること自体は典型的なものであるため、正解した受験生も多かったことでしょう。
(1)
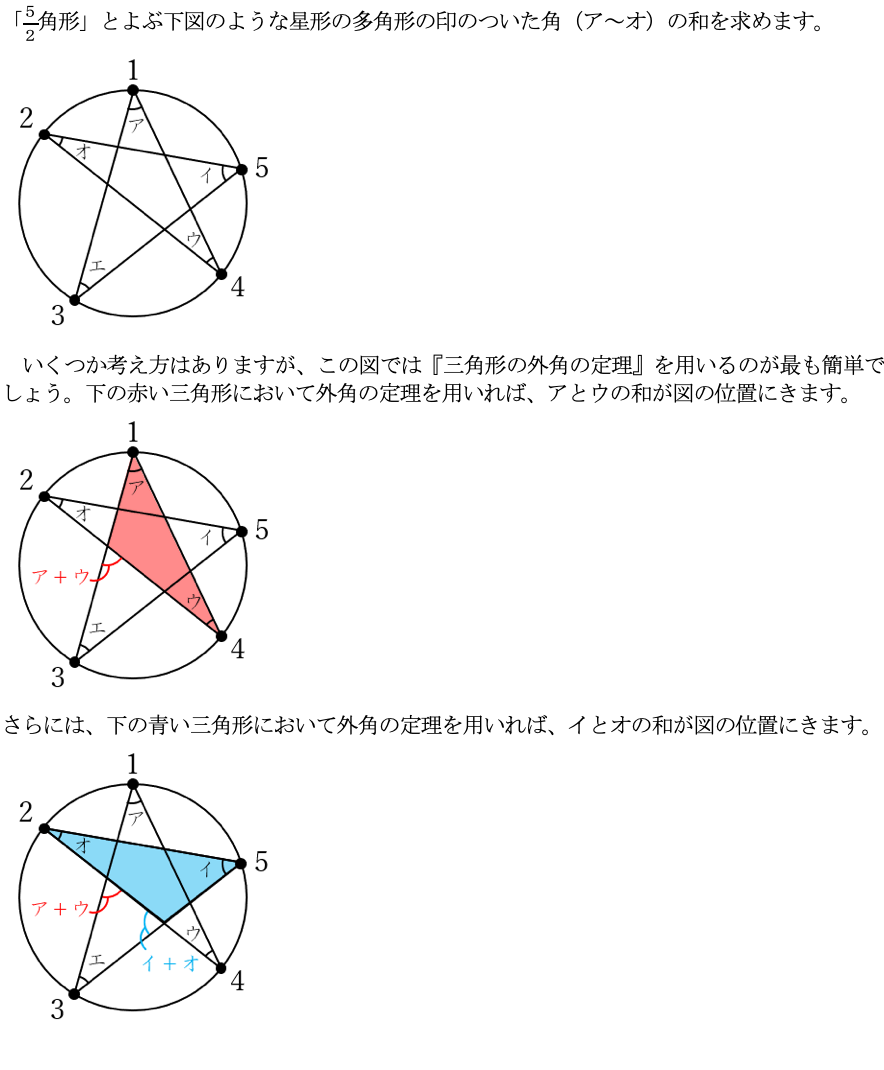
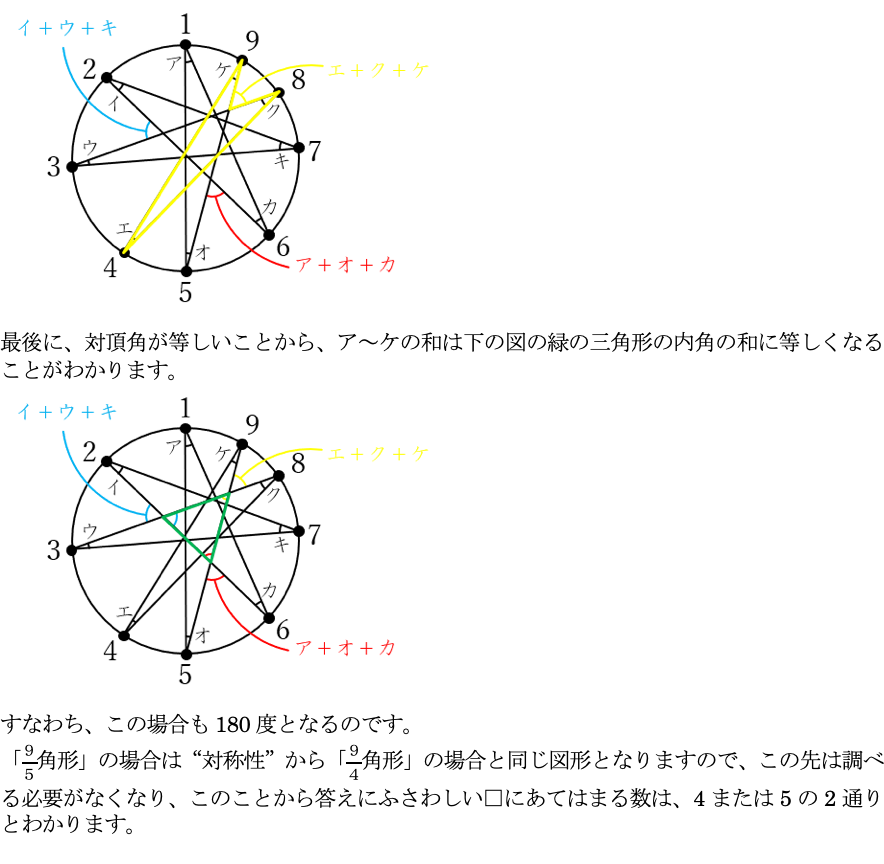
よって、ア~オすべての和は、下図の黄色い三角形の内角の和に等しいことがわかります。
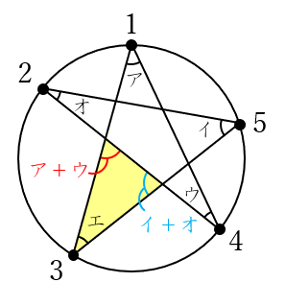
つまり、ア~オの和は180度と求まります。
なお、この問題で問われている答え(星形の先にある5つの角の和)は暗記している受験生も多いはずなので、その受験生にとっては(1)は数秒で正解できたことでしょう。
(2)

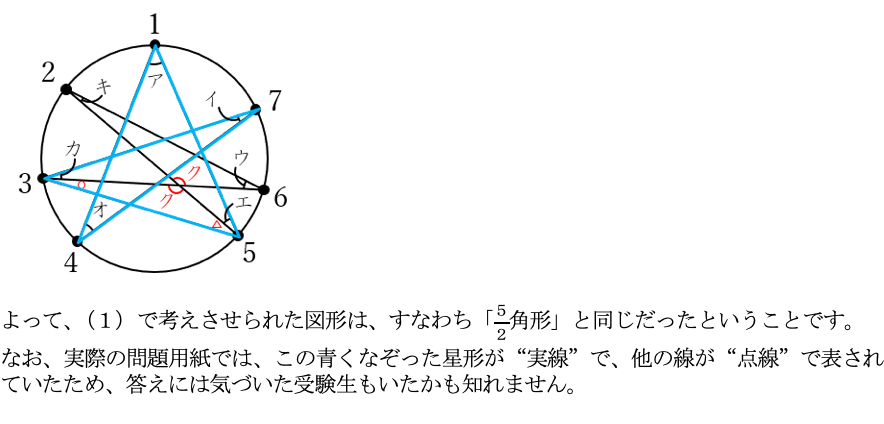
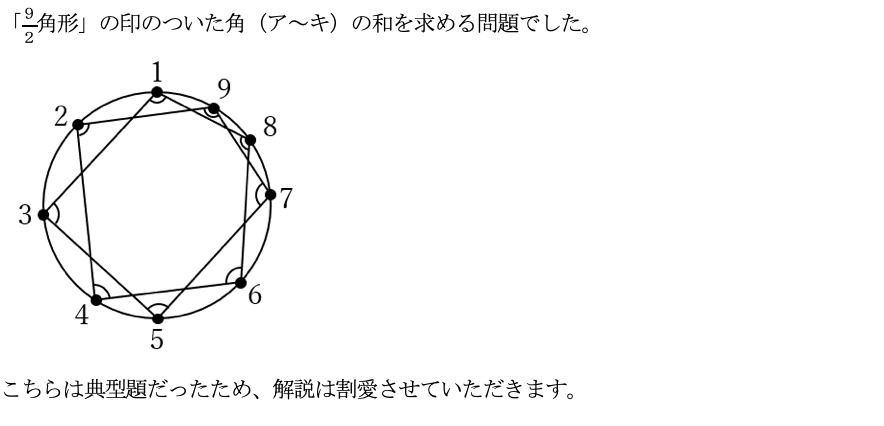
(3)
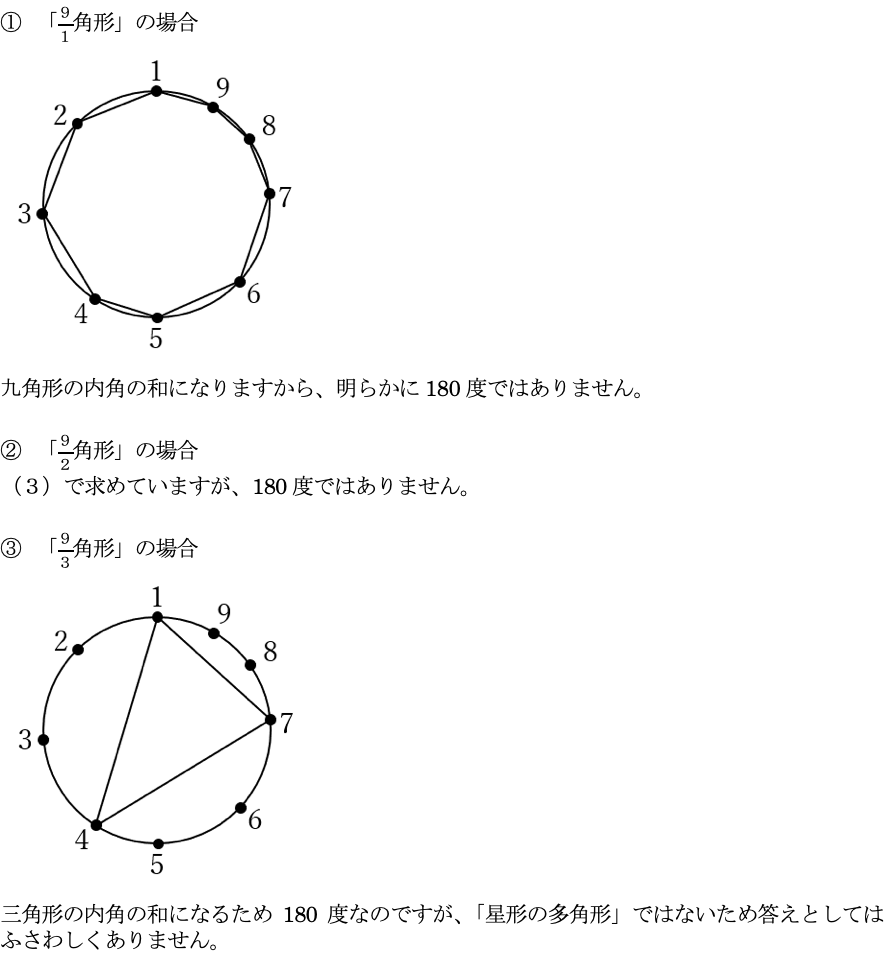
(4)

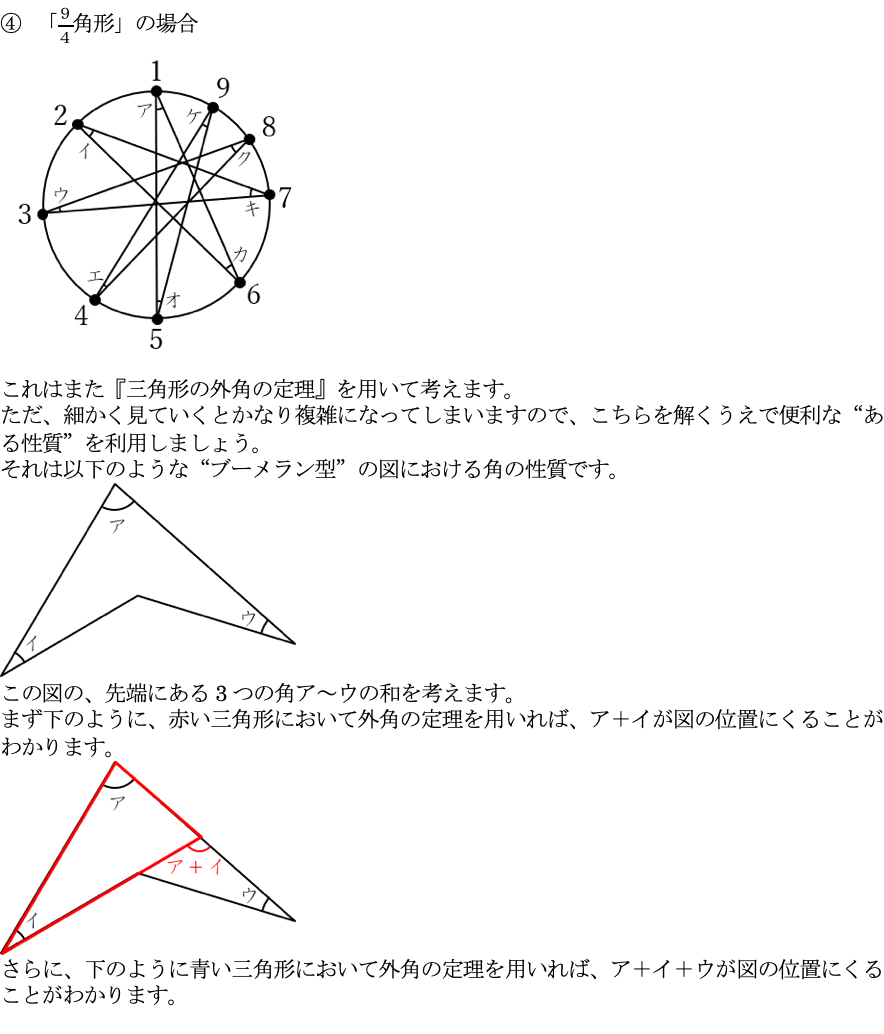

浅野中入試対策・関連記事一覧
浅野中入試対策・同じ教科(算数)の記事
浅野中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)