算数の合否を分けた一題
浅野中入試対策・算数の合否を分けた一題(2019年度)
難易度分類
| [1] | (1) A (2) イ A ウ A (3) エ A オ A(4) カキ A クケ A (5) コ B サ B |
|---|---|
| [2] | ア A イ A ウ A エ B オ B~C |
| [3] | (1) A (2) A (3) B |
| [4] | (1) A (2) B (3) B (4) B |
| [5] | (1) A (2) A (3) B (4) B (5) B |
A…浅野中合格を目指すなら、確実に得点したい問題
B…知識、解法次第で、得点や所要時間に大きく差がつく問題
C…難度、処理量から判断して、飛ばすことも検討すべき問題
2019年度 出題総評
形式面では例年と大きな変化はなく、計算・小問集合を含め大問5題の構成となりました。
学校発表の合格者平均得点率は84.8%、受験者平均得点率は70.1%。年度による得点率のブレがやや大きめである浅野中算数の中でも、本年度はかなり易しめに振れています。
浅野中合格レベルの受験生にとっては試験時間内で解き切るのが難しいと思われる問題は無く、ミスの多寡が合否を分ける大きな要因となったのではないかと思われます。
問題別寸評
2018年度同様、計算問題と小問集合をまとめた形で大問1として出題されました。
(1)
例年同様の逆算タイプの計算問題です。浅野中の計算問題としてはやや取り組みやすいと思われます。確実に正解しておきたいところです。
(2)
前半が消去算、後半がつるかめ算という、よくありそうでいて意外と珍しい問題です。
それぞれの内容は基本的なもので、これも落とせません。
(3)
前半部分は、不足が共通になっている余りの問題(根本原理ポイント365 実践編187)。「2の倍数にも3の倍数にも1不足する数」ととらえるのが定石です。
後半は、初めの何個かを書き出して規則性を見出すのが良いでしょう。
前半部分にあてはまる整数を小さいほうから書き出すと、
5,11,17,23,29,35,41,47,53,59,65…
これらを5で割ったときの余りは
0,1,2,3,4,0,1,2,3,4,0…
のように、5つごとに循環していることを利用して求めます。
浅野受験生にとっては標準的な問題です。
(4)
正確でない時計を題材とした典型的な出題です。
Aは一日に80分遅れるので、正しい時間で1日=1440分の間に1440-80=1360分だけ進み、Bは一日に48分進むので、1440分の間に1440+48=1488分の時を刻みます。
すなわち、正しい時間:Aが進む時間:Bが進む時間=1440分:1360分:1488分=90:85:93です。
問われている時刻までに、時計Aは255分進んでいることから解答が得られます。
(5)
与えられた投影図で表されているのは、下の図のような立体です。
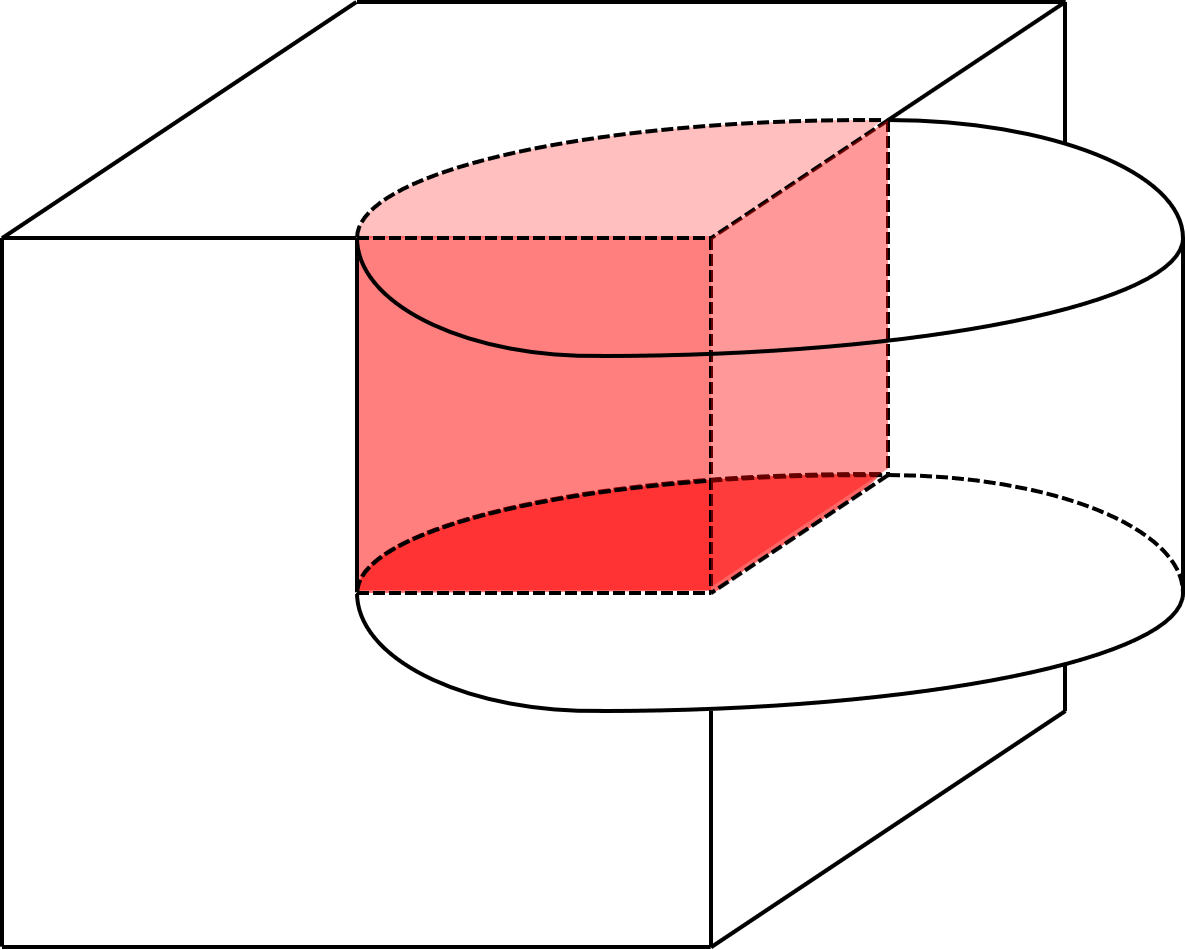
立方体と円柱が重なった部分は、図に赤く示した、円柱の1/4にあたる立体です。
求める体積・表面積は、もとの立方体や円柱の体積・表面積から、赤い立体の体積や表面積の一部を引くことで求めることが出来ます。
立体をとらえることが出来れば、体積の方はそれほど難しくありませんが、表面積を求めるときにはミスが出そうです。
自然数の和の公式、1+2+3+…+n=(n+1)×n÷2は、中学受験生必須の知識ですが、平方数の和、1×1+2×2+3×3+…+n×nの値を求める公式は高校数学の範囲です。
ただ、適切な誘導によって受験算数の範囲で考えることは可能で、本問で用いられているのも、比較的よく知られた方法です。
類題を経験していた受験生には有利に働いたことでしょう。
アは自然数の和の公式から容易です。
イとウについても、題意がつかめていれば問題ありません。
ここまでの流れから、図5に示された3枚の紙に書かれた整数の和が、どの位置でも41になっていることに気がつけば、エとオも解答できます。
(1)
問題の条件に沿って計算するだけですが、「46個以上の場合は45個のときと1個の売り値は同じ」という条件を読み落とした受験生もいそうです。
50個のときの売り値は45個のときと同じで、25個のときよりも5×(45-25)=100円安くなっているので、ア=200-100=100円です。
これが得られれば、イは100×50=5000円と容易に求まります。
(2)
(1)の結果から、この菓子は25個買っても50個買っても代金が5000円で等しいという、少し変わった状況になっていることが分かります。
もう少し詳しい状況をつかむために、50個から個数を減らしていくとどうなるかを調べてみましょう。
| 個数 | 売り値 | 代金 |
|---|---|---|
| 25 | 200 | 5000 |
| 26 | 195 | 5070 |
| 27 | 190 | 5130 |
| … | … | … |
| 43 | 110 | 4730 |
| 44 | 105 | 4620 |
| 45 | 100 | 4500 |
| 46 | 100 | 4600 |
| 47 | 100 | 4700 |
| 48 | 100 | 4800 |
| 49 | 100 | 4900 |
| 50 | 100 | 5000 |
上の表のように、45個のときまでは売り値が100円で一定のため、個数が減ると代金も安くなりますが、44個以下に減らすと売り値が増えてしまうために代金は高くなることが分かります。
(3)
算数としてきちんと解くためには面積図を用いて考えるのが有力ですが、やや難しく、受験生にとっては浮かびにくいかと思われます。
試験の現場では、(2)で考えたように調べ上げていく方が現実的でしょう。25個から個数を増やしていくと、しばらくの間は代金が増えていくようですので、先をどんどん調べてみましょう。
| 個数 | 売り値 | 代金 |
|---|---|---|
| 25 | 200 | 5000 |
| 26 | 195 | 5070 |
| 27 | 190 | 5130 |
| 28 | 185 | 5180 |
| 29 | 180 | 5220 |
| 30 | 175 | 5250 |
| 31 | 170 | 5270 |
| 32 | 165 | 5280 |
| 33 | 160 | 5280 |
| 34 | 155 | 5270 |
| 35 | 150 | 5250 |
上の表のように調べていくことによって、32個と33個のときに5280円と最も高くなり、その先は個数を増やすと代金は減っていくことが分かります。
3人までのじゃんけんの出題はよく見られますが、4人という設定はやや珍しいところです。浅野中の場合の数としては、標準的な難度だと思われます。
(1)
A、B、C、Dの4人とも3通りずつの手の出し方があるので、積の法則を用いて、
3×3×3×3=81通りと求められます。
これは是非とも正解したいところです。
(2)
4人のうち勝つ2人の選び方は、組合せの計算で、
4×3÷(2×1)=6通りです。
さらに、勝つ2人の手はグー、チョキ、パーの3通りあり、勝つ2人の手を決めれば負ける2人の手は自動的に定まるので、4人の手の出し方は、
6×3=18通りと求められます。
(3)
グーを出した人が勝つということは、残りの人はチョキを出していると決まります。
グーを出す人の人数で場合分けをすれば分かりやすく求められます。
グーを出すのが1人のとき→4人から1人を選ぶ場合の数は4通り。
グーを出すのが2人のとき→4人から2人を選ぶ場合の数は6通り。
グーを出すのが3人のとき→4人から3人を選ぶ場合の数は4通り。
グーを出すのが4人のときはあいこになってしまうので、問題に適しません。
よって、4+6+4=14通りが答えとなります。
(4)
4人の手の出し方の組み合わせは、
(グー、グー、チョキ、パー)、(グー、チョキ、チョキ、パー)、(グー、チョキ、パー、パー)の3通りが考えられます。
このうち、たとえば(グー、グー、チョキ、パー)のときを考えてみましょう。
チョキを出す人の選び方が4通り、残りの3人からパーを出す人の選び方が3通り、残りの2人はグーと自動的に定まるので、4人の手の出し方は4×3=12通りです。
他の手の組み合わせの場合も同様なので、12×3=36通りが正解です。
また、余事象に注目して求めるのも有力です。
4人の手が1通りの手に揃ってあいこになる場合は、グーかチョキかパーのどれに揃うかを考えて3通り。
4人の手が2通りに分かれて勝負がつくのは、(3)で考えた14通りのほか、チョキを出した人が勝つ場合とパーを出した人が勝つ場合を考えれば良いので、14×3=42通り。
以上にあてはまらない場合が(4)で求めたい場合の数なので、(1)で求めてあるすべての場合の数から引いて、
81-(3+42)=36通り。
合否を分けた1題
大問5を取り上げます。
2017年2月、東京大学入学試験の数学(文科各類)で出題された問題が元ネタになっています。(1)~(3)の誘導をつけた上で、問題の本質部分は変えないまま、中学受験生にも解決可能な形に改題されています。
2017年4月には、受験ドクター講師ブログの拙稿にて、本問(4)とほぼ同じ形で紹介をしていました。
(1)
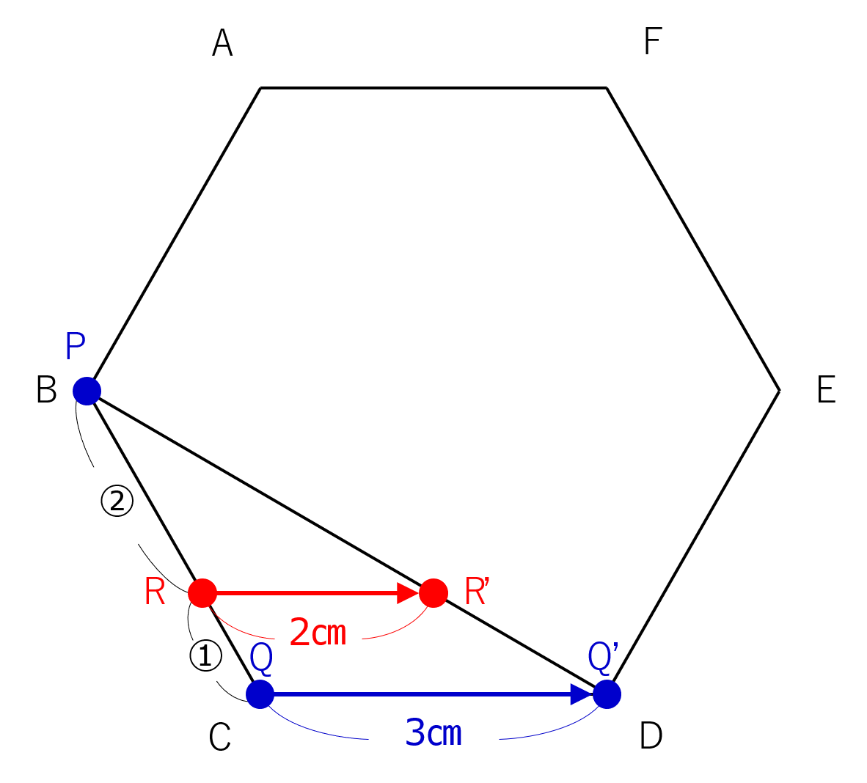
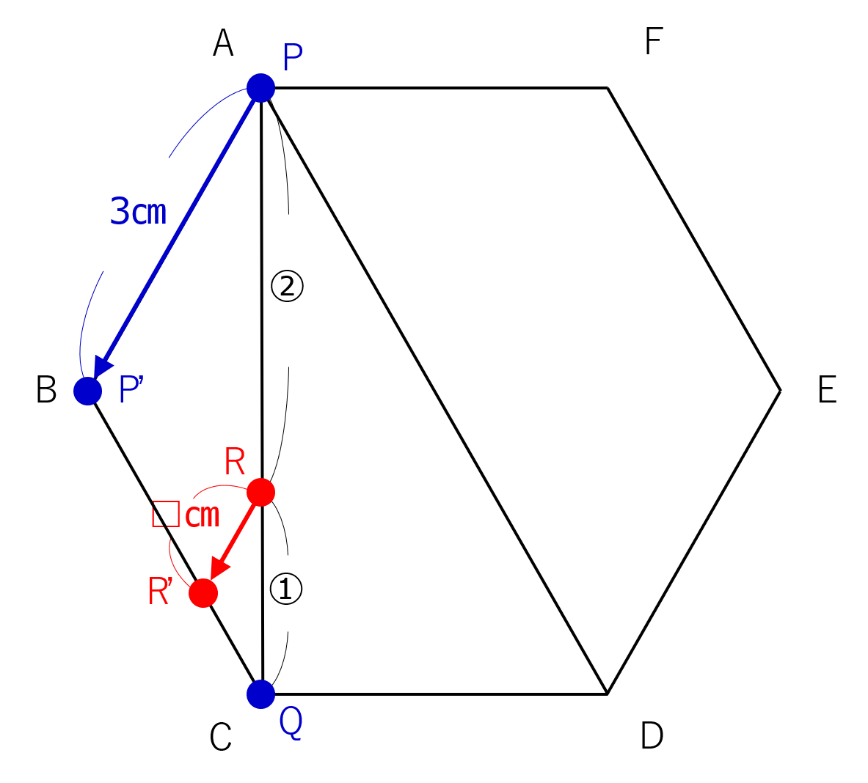
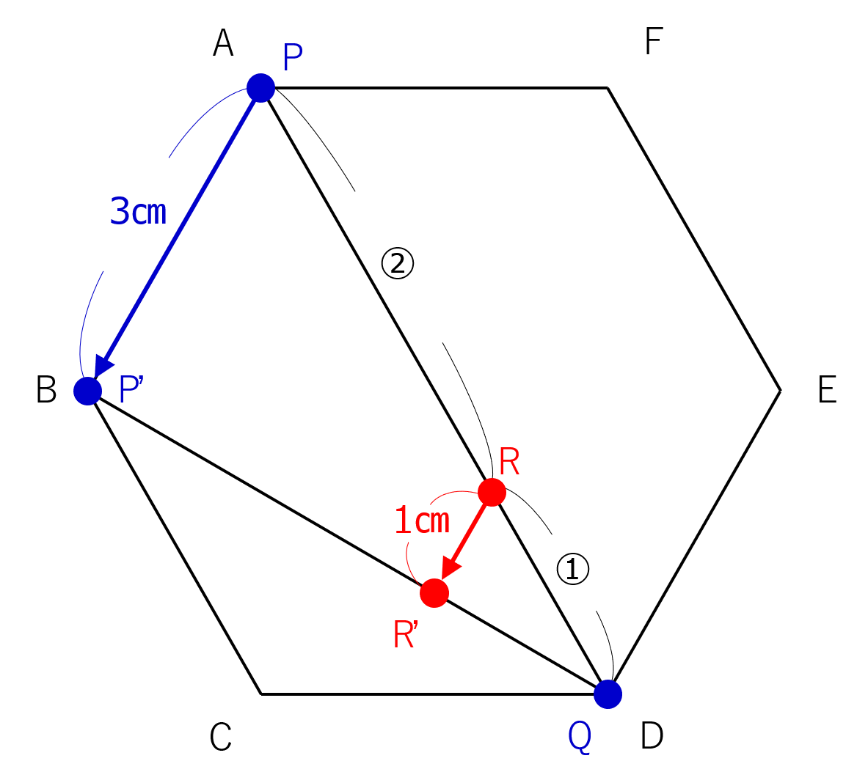
問題に与えられた状況を下のように図に描ければ、あとは容易です。
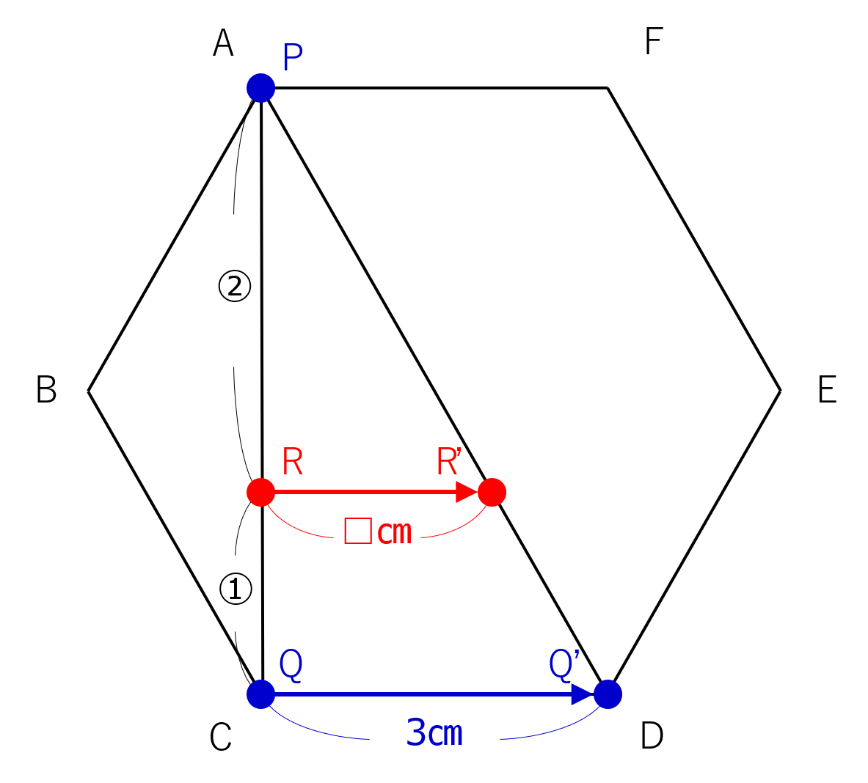
図で、三角形PQQ’と三角形PRR’は相似で、相似比は3:2になっています。
点Rが動く線の長さであるRR’=3cm×2/3=2cmです。
(2)
今度は、三角形QPP’とQRR’の相似比が3:1になっているので、RR’=3cm×1/3=1cmです。
(3)
(1)(2)では、
・点Pが点Aに止まっていて、点Qが辺CD上を動く場合
・点Qが点Cに止まっていて、点Pが辺AB上を動く場合
を考えましたが、他に、
・点Pが点Bに止まっていて、点Qが辺CD上を動く場合
・点Qが点Dに止まっていて、点Pが辺AB上を動く場合
を図に描いてみましょう。
(1)(2)で考えたのと合わせ、4つの場合にRが動いた線を解答用紙に与えられた図に書き込みむと、下図のようになります。
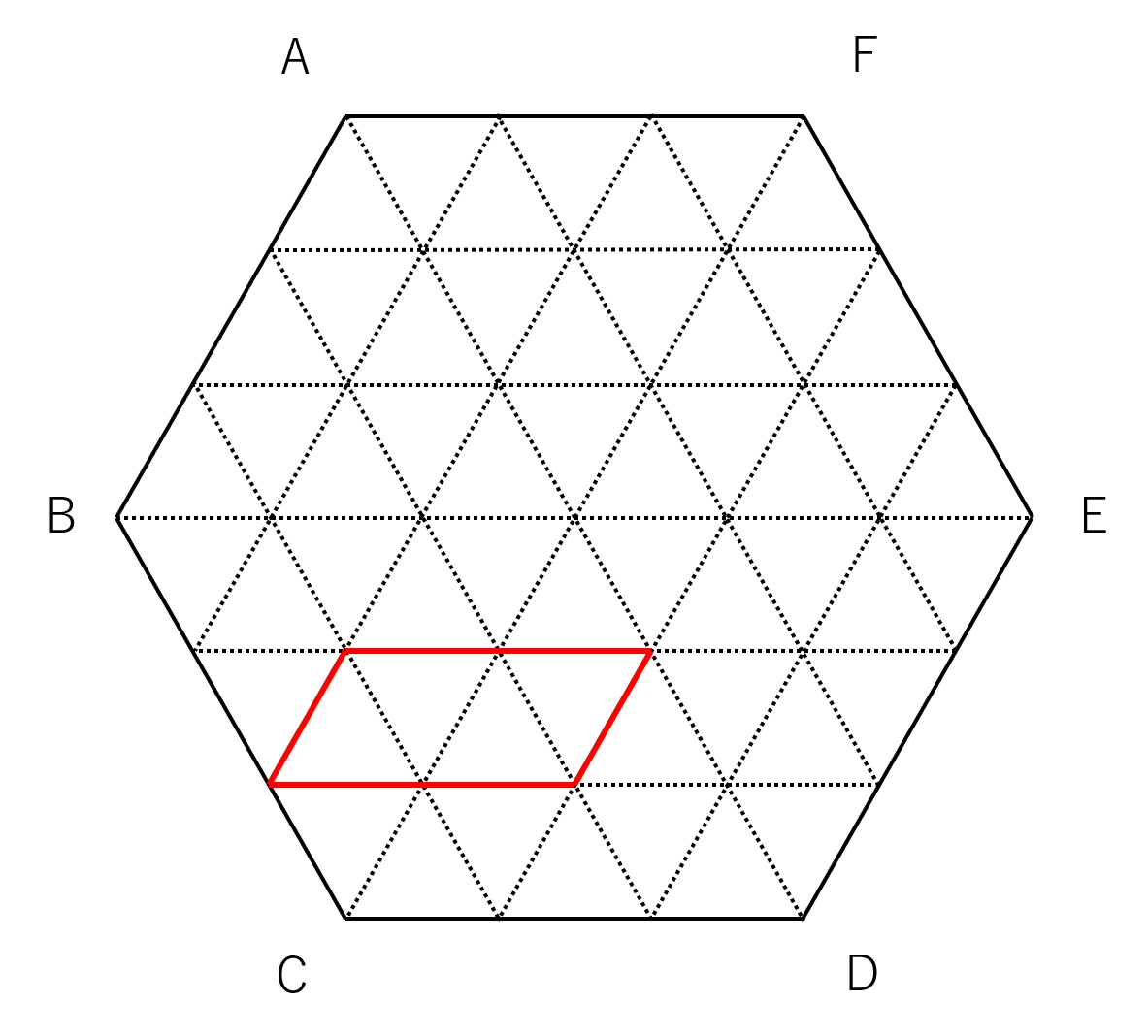
点Rが動くことができる範囲は、この平行四辺形の周上と内部になります。
問題の指示に従って、内部を斜線で示せば答えとなります。
(3)が出来れば、ここは容易です。
(3)の図で、正六角形全体は小さな正三角形54個に分割されています。そのうち、Rが動く範囲として斜線で示したのは小三角形4つ分です。
![]()
(3)で求めた範囲のうち、辺EFに最も近いのは下図の赤い点で示した位置です。
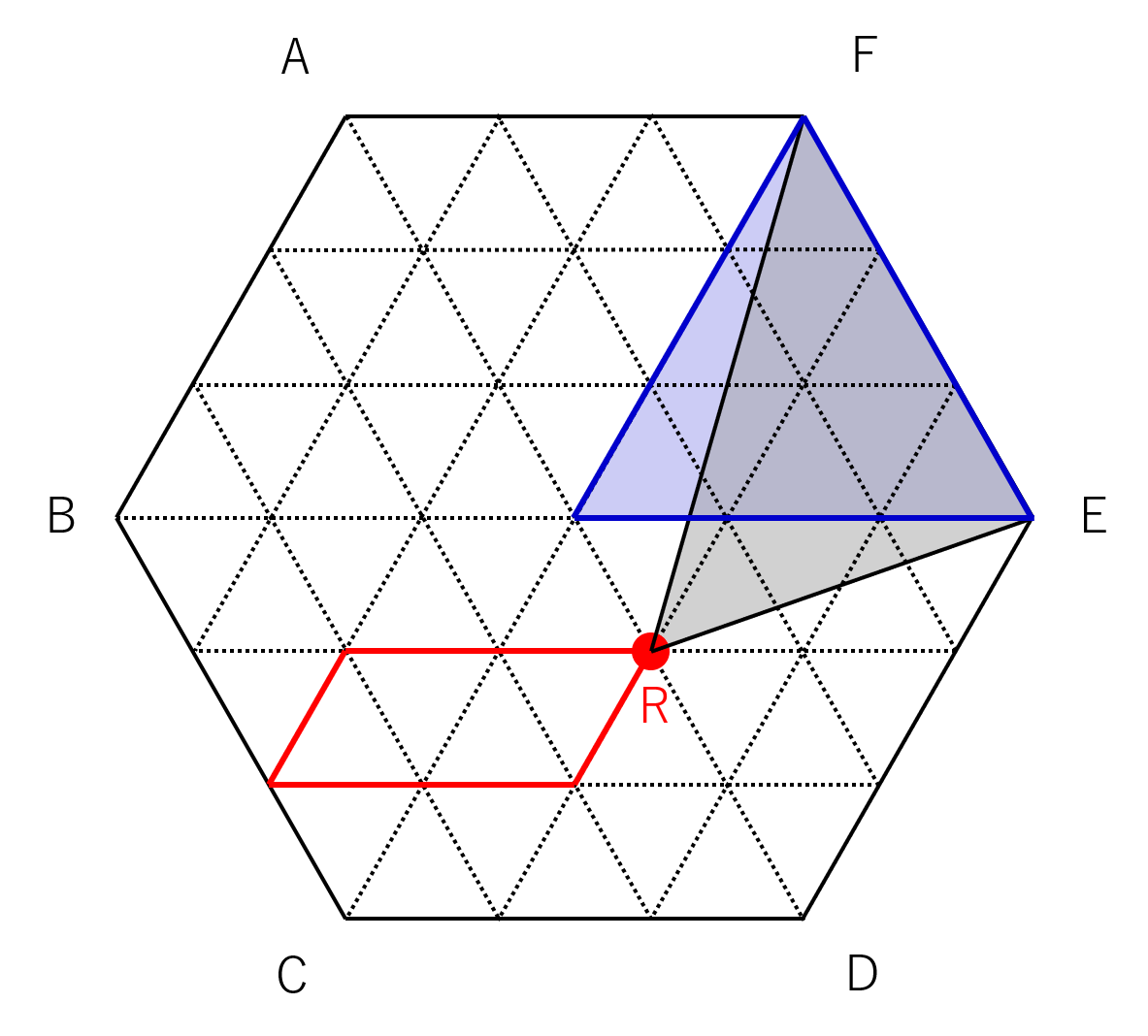
したがって考えられる三角形EFRのうちで面積が最も小さくなるのは、図に灰色で示した三角形です。
このまま求めることも可能ですが、等積変形を行って図の青い三角形の面積を考えるのが良いでしょう。この面積は明らかに正六角形ABCDEFの![]() です。
です。
浅野中入試対策・関連記事一覧
浅野中入試対策・同じ教科(算数)の記事
浅野中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)

 (2 votes, average: 4.50 out of 5)
(2 votes, average: 4.50 out of 5)