算数の合否を分けた一題
浅野中入試対策・算数の合否を分けた一題(2018年度)
難易度分類
| [1] | (1)A (2)A・A (3)B (4)A・B (5)B・B |
|---|---|
| [2] | (1)A (2)B・B・B |
| [3] | (1)A・A・B (2)B (3)B |
| [4] | (1)A (2)B (3)B~C |
| [5] | (1)B (2)B (3)B |
A:浅野合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき
出題総評
出題形式は、計算1問、一行問題5問、大問4題と例年とほぼ同じ構成になりました。難易度も標準的なものからやや難しいレベルのものが出題され、場合の数・立体表面の最短距離・相似・速さとダイヤグラムなど、やや処理に時間を要する問題が何問か見られました。
問題別寸評
例年[1][2]と分けて出題されていた計算と小問集合が[1]にまとめられましたが、受験生にとって大きく戸惑うほどのことはなかったでしょう。
(1)
計算途中では数値がきれいになりそうな予感をさせつつも、結局あまりきれいな答にならないことから、やや不安になった受験生もいるかもしれません。
ともあれ、浅野中の計算問題としては標準的で、ここは落とせません。
(2)
180度よりも大きな内角を持つ11角形ですが、内角の和は180°×(11-2)=1620°…イと求められることに変わりはありません。これが求められればウも容易です。
(3)
意外とやっかいな通過算です。
列車Bが列車Aに追いついてから追い抜くまでに25秒かかるという条件をどう扱うのがポイントです。
列車Bに追いつかれるまでの間に列車Aは17×25=425m進みます。これに列車Aの長さである55mを加えた480mのトンネルを、列車Bが25秒で通過すると考えることにより、もう1つの条件と合わせれば、典型題として処理することが出来るようになります。
試験場では、与えられた2つの条件から、
エ×21=388+オ
(エ-17)×25=55+オ
と立式し、消去算として求める方が現実的かもしれません。
(4)
カは基本的な出題です。
キのように、長針と短針がある直線に対して対称な位置に来る時刻を求める問題では、長針と短針の進んだ角度の和に注目するのがポイントです。
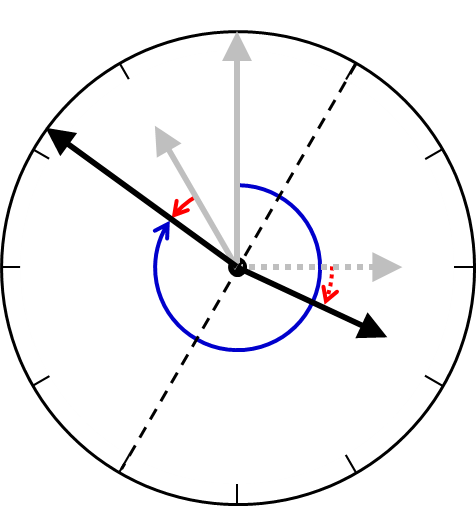
図のように、3時のときの短針を文字盤の1と7を結ぶ直線に関して対称に移動すると、11時の位置から反時計回りに回転する針になります。この針と長針が出会うときが求める時刻であり、3時からこの時刻までに2本の針が動いた角度の和は300°です。
時計算の応用問題として練習した経験のある受験生が多いはずですが、試験では差のつくところでしょう。
(5)
クとケで問われていることの違いがピンと来ず、戸惑った受験生がいたかもしれません。
クは9を3つの整数の和に分解する方法の数を求める問題です。
(1,1,7) (1,2,6) (1,3,5) (1,4,4) (2,2,5) (2,3,4) (3,3,3)の7通り。
一方、ケの方は上記の7通りの分け方のそれぞれに対し、3人のうち誰が何個もらうかまで考えなければなりません。
3人をA,B,Cとすると、例えば(1,1,7)に対しては、(A,B,C)=(1,1,7) (1,7,1) (7,1,1)の3通りの分け方があります。
(1,2,6)のように3つの数がすべて異なる場合には6通り、(1,1,7)のように3つの数のうち2つが同じ場合には3通り、(3,3,3)のように3つの数全てが同じ場合には1通りの分け方があることを確認し、慎重に足し合わせましょう。
4つの装置のうち、装置Dの振る舞いがやや捉えづらいかもしれません。
(1)
題意を確認する小問です。
アは、2回かけても300を超えない最大の整数を求めることになります。
17×17=289、18×18=324より、ア=17です。
イは、アの値を装置Aに入力する、つまり2回かけることになります。17×17=289です。
ウは、ア・イと比べると装置Dの振る舞いが理解しにくく、難しく感じた受験生も多かったことでしょう。
与えられている装置Dの説明をよく読むと、ウの値は、装置Bに入力したときに19が出力されるような整数の個数であることが分かります。
装置Bに入力して19が出力されるのは、19×19=361以上20×20=400未満、すなわち361~399の整数です。この個数は、399-361+1=39個です。
(2)
結局のところ、装置Cとは「入力した整数以下で最も大きい平方数を出力する装置」であることを確認して下さい。
16=4×4であり、次に大きい平方数は25ですから、◇として16~24の整数を入力したときに16が出力されます。
(3)
☆が1以上6以下と限定されていますので、☆の値1~6までに対して◎としてどのような整数が当てはまるか調べていくのが良いでしょう。
☆=1のとき、◎-B→☆となる◎は、1×1以上2×2未満の整数ですから1~3です。また、☆-D→◎となる◎は、Dの振る舞いから先の1~3の個数ですので3です。よって、☆=1に対して◎=3が当てはまります。
☆=2のとき、◎-B→☆となる◎は4~8、☆-D→◎となる◎は4~8の個数である5で、◎として5が得られます。
☆=3のとき、◎-B→☆となる◎は9~15、☆-D→◎となる◎は9~15の個数である7ですが、これらに共通する◎はありません。
☆=4~6のときにも、◎-B→☆となる◎と、☆-D→◎となる◎に共通なものはありません。
以上のように調べることによって、◎に当てはまる整数は3と5であることが分かりました。
(1)は比較的基本的ですが、(2)(3)ではつるかめ算の考え方を用います。特に(3)が考えづらいでしょう。
(1)
速さの比と時間の比の関係を使うのが良いでしょう。
魚Aが水そうを1周するのに、流れがない状態では15秒、反時計回りに毎秒2cmの流れを作ったときには20秒かかります。この時間の比は3:4ですから、速さの比は④:③になっています。
流れのあるときにはその分だけ進む速さが遅くなっているので、④-③=①が毎秒2cmに当たります。よって、魚Aの速さは④=毎秒8cmです。
(2)
(1)より、水そう1周の長さは、毎秒8cm×15秒=120cmです。
また、毎秒2cmの流れを作ったときに魚Aが進む速さは8-2=毎秒6cm、毎秒1cmの流れのときには8-1=毎秒7cmです。
まとめると、毎秒6cmと毎秒7cmの速さをあわせて18秒で120cm進んだことになります。これは典型的なつるかめ算の形です。
(3)
浅野中受験生であれば、つるかめ算の応用として、「りんご、みかん、なしを合わせて30個、みかんとなしの個数の比が2:1になるように買う」ような設定の問題に触れたことがあるでしょう。
本問でも、3種類の進み方のうち2種類の時間の比が与えられており、上記のつるかめ算と本質的には同じ問題ですが、速さとの融合になっている分、解法が思い浮かびにくかったと思われます。
| 流れ | 魚Aが進む速さ | 時間 |
|---|---|---|
| 反時計回りに毎秒2cm | 時計回りに毎秒6cm | |
| 時計回りに毎秒1cm | 反時計回りに毎秒7cm | ① |
| 反時計回りに毎秒1cm | 時計回りに毎秒7cm | ② |
まずは、時間の比が分かっている2種類の進み方について、その間の平均の速さを求めます。
時計回りに毎秒1cmの流れを1秒間、反時計回りに毎秒1cmの流れを2秒間作ったと考えてみましょう。
最初の1秒間では、反時計回りに7×1=7cm進み、次の2秒間では時計回りに7×2=14cm進みます。結局、この3秒間で時計回りに14-7=7cm進んだと考えられ、この間の平均の速さは毎秒![]() cmです。
cmです。
このことから、「毎秒6cmと毎秒![]() cmを合わせて25.5秒で120cm進んだ」という設定のつるかめ算と同様に考えれば、答えが得られることが分かります。
cmを合わせて25.5秒で120cm進んだ」という設定のつるかめ算と同様に考えれば、答えが得られることが分かります。
浅野中頻出の立体切断です。本校の立体切断の出題としては比較的穏やかな内容でした。
(1)
まずは、立方体の同一面上にあるMとNを通る直線を延長し、辺BA・BCの延長と交わる2点を取ります。
その後、これらの2点とFを結ぶことにより、切り口の線と辺AE・CGとの交点が得られます。
切り口Sは下図のような五角形になりますが、「切り口の辺以外のものは書いてはいけない」というただし書きに注意が必要です。解答用紙には、立方体の外に延長した補助線を書いてはいけません。
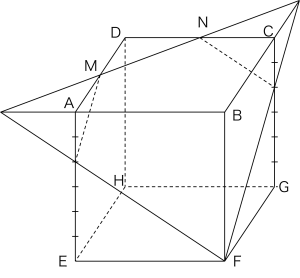
(2)
Fを頂点とする大きな三角すいから、立方体の外に飛び出した小さな三角すいを2つ引くことで求められます。(1)が正解できる受験生にとっては、ここも落としたくないところです。
(3)
切り口Tも描くと下図のようになります。
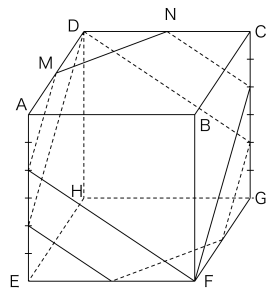
ここで、切り口Tの向こう側にある点Hを含む立体は、(2)で求めた点Bを含む立体と全く同じものになっています。
よって、切り口SとTにはさまれた立体Vの体積は、立方体全体の体積から(2)の答の2倍を引くことで求められます。
合否を分けた一題
学校発表の平均得点率は63.2%、合格者の平均得点率は76.9%でした。年度によって平均得点率のばらつきが目立つ本校ですが、本年度の出題はやや易しめに振れたと言えるでしょう。
誰もがスラスラと解ける問題ばかりではありませんが、例年、数問程度混じっている極端な難問はほぼ見当たらず、出題のほとんどが受験生の力によって大きく差のつくものでした。
合否を分けた一題としては、[2]を取り上げます。
難易度そのものとしては標準的な出題であり、合格のためには完答しておきたいところですが、(2)では解法によって正解率や消費時間に差がついたものと思われます。
(1)
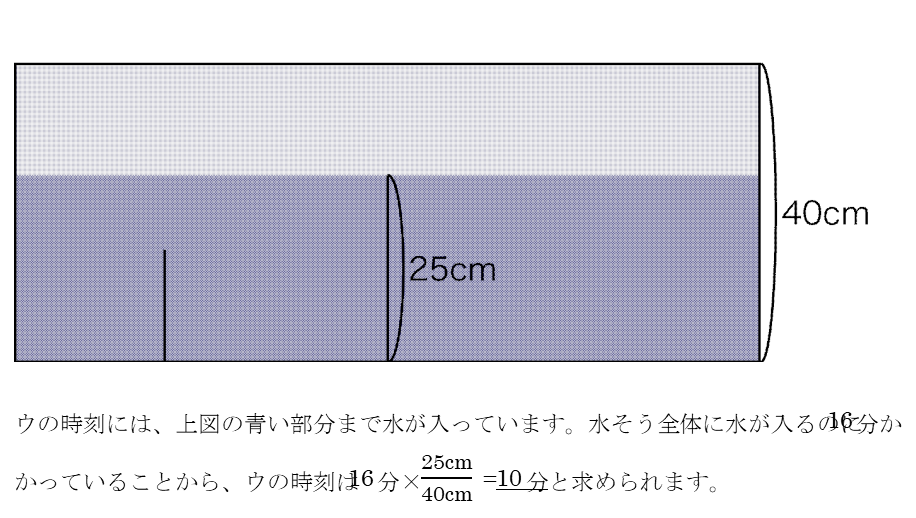
水そう全体に水が入るのに16分かかっていることから、
30×80×40÷16分=6000cm^3/分→毎分6Lと求められます。
(2)
板AとBの高さが図3や4には示されず、問題文の中だけに与えられています。図形問題ではつい図に目が行きがちですが、問題文にのみ書かれた条件がないかどうか注意が必要です。
この条件を読み落としていなければ、水量変化の問題としては標準的です。
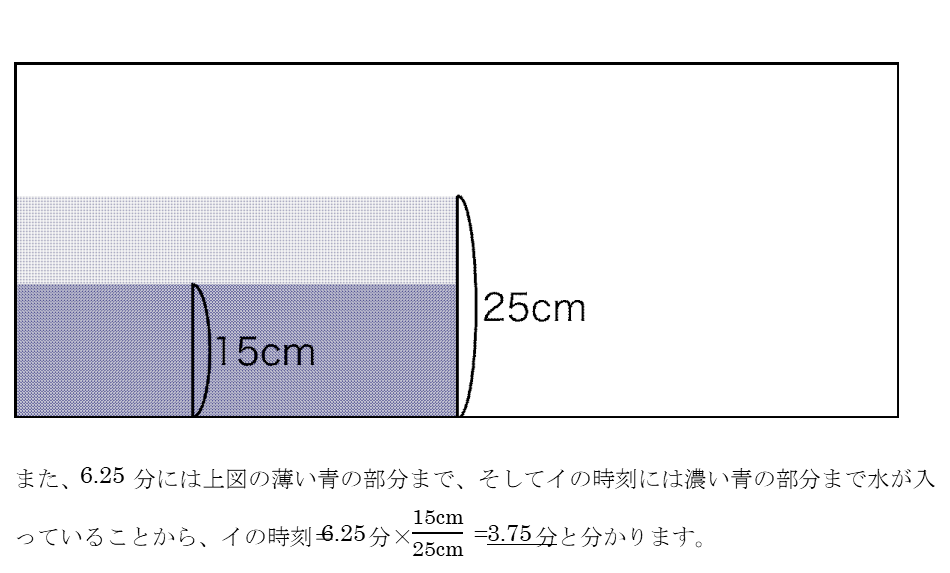
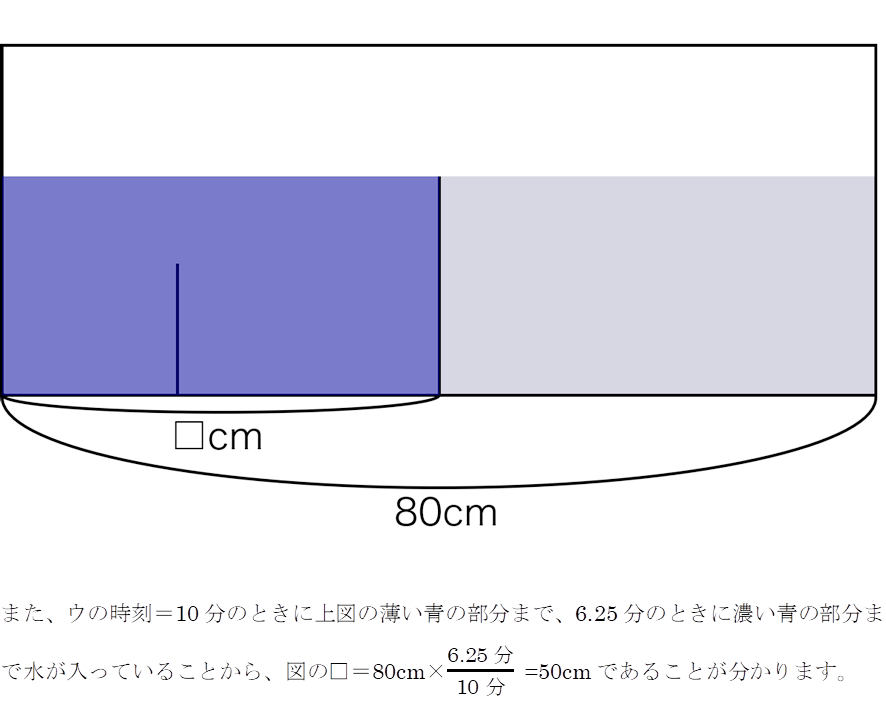
(1)を利用し、水量に注目して求めていくのが一般的ですが、以下のように比を利用してウ→イ→アの順に解き進められれば、時間の節約になるでしょう。
浅野中入試対策・関連記事一覧
浅野中入試対策・同じ教科(算数)の記事
浅野中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 算数の合否を分けた一題(2017年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)