算数の合否を分けた一題
浅野中入試対策・算数の合否を分けた一題(2017年度)
難易度分類
| [1] | A |
|---|---|
| [2] | (1)A (2)A (3)A (4)A (5)B |
| [3] | (1)A (2)B (3)B |
| [4] | (1)B (2)B (3)B |
| [5] | (1)B (2)B (3)C |
| [6] | (1)A (2)B (3)B (4)C (5)C |
A:浅野合格を目指すなら必ず得点したい問題
B:着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C:難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題
出題総評
出題形式は、計算1問、一行問題5問、大問4題と例年とほぼ同じ構成になりました。難易度も標準的なものからやや難しいレベルのものが出題され、場合の数・立体表面の最短距離・相似・速さとダイヤグラムなど、やや処理に時間を要する問題が何問か見られました。
問題別寸評
計算問題が1問出題されました。小数と分数の混じった四則計算です。確実に正解したいところです。
一行問題7問から成る小問集合です。文章題、場合の数、平面図形と出題単元は多岐に渡っています。
(1)
倍数変化算です。もらった金額が異なるので解法が身についているかがポイントです。
(2)
周期の問題です。細かい部分は書き出して確認して解いていきましょう。
(3)
周期と暦の問題です。(2)と同じタイプの出題でしたので、こちらも確実に解いておきたいところです。
(4)
消去算の問題です。箱の代金が入るので少し複雑になっています。答えを出したあとに代入して見直しをしたいところです。
(5)
平面図形と相似形の問題です。補助線を引いて相似形を作ることができたかがポイントです。また、辺の比から面積比へとつなげられるように、普段から練習しておきましょう。
互除法を用いた、数の性質に関する問題です。過去、開成中や筑駒中でも出題された題材でもあります。
(1)
ダイヤグラムを用いた速さの問題です。休む回数に気を付けて確実に正解したい問題です。
(2)
追い越す回数が3回となる速さの範囲を求める問題です。与えられたダイヤグラムを利用して、条件に合う動きを見つける必要があります。
(3)
(2)でB君の動きがわかっていれば後は計算して数値を求めていく問題になります。(2)が解けた人は確実に正解しておきたいところです。
(1)
二等辺三角形に内接する円を用いた相似形の問題です。他の学校でも円すいに内接する球という形で出題されたこともあり、目にしたことがある受験生もいたものと思われます。
この問題のポイントは、三角形に接する部分に向けて補助線を引けたかどうかです。この半径により、この後の問題の正解が決まります。
(2)
内接円の半径を求める問題です。(1)の答えと、与えられたヒント(3:4:5の直角三角形)から、二等辺三角形の高さにつなげられたかがポイントでした。
(3)
二等辺三角形と円の両方に接する円の半径を求める問題です。円と円の間に補助線を引き、相似形を作ることで正解を出すことができます。
(1)
カードを選んで引き算の式を作る、場合の数の問題です。(1)は1ケタ-1ケタとなる場合で、調べやすかったと思われます。問題文の条件の確認も併せてしっかり正解しておきましょう。
(2)
カードの枚数が増えたので、「2ケタ-1ケタ=1ケタ」となることをまず気づく必要があります。後半の問題を考えると、ここも正解しておきたいところです。
(3)
数字を5枚使うので、「2ケタ-1ケタ=2ケタ」となる場合と、「2ケタ-2ケタ=1ケタ」となる場合とに分けて考える必要があります。正確に調べるには時間を要しますので、大問6の前半を解いてから戻ってくる選択も必要かと思われます。
(1)
直方体から4つの三角すいを切り取ってできる立体についての問題です。最初は体積を求める問題です。この辺りは確実に正解しておきましょう。
(2)
最短距離になるように引いた直線の長さの和を求める問題です。最短距離は展開図で考えるという解法が身についているかどうかが試されます。ただし、展開図を描くのが少し難しいため正解率は低くなったものと思われます。
(3)
(2)とつながる問題で、辺の比を求めます。こちらも展開図が描ければそんなに難しくはないのですが、前述の通り展開図が描きにくかったので解きづらい問題でした。
(4)
(1)で求めた三角すいをさらに切断した立体の体積を求める問題です。(5)につながる誘導問題ですが、ここまで正解するのも難しかったため、正解率は低いものと思われます。
(5)
(4)からつながる問題で体積を求める問題です。(4)をヒントにして、もう片方の体積を求める必要があります。今回の入試問題の中で屈指の難問でした。
合否を分けた一題
最初に述べましたが、今年の浅野中の出題形式は例年通りであったものの、図形・場合の数が少し難しかったです。限られた解答時間の中でどの問題を確実に正解したかが合否を決めるといってもよいでしょう。今回はその中から補助線の引き方がポイントとなった[4]を説明してまいります。
(1)
三角形ABDと三角形AGEについて考えます。
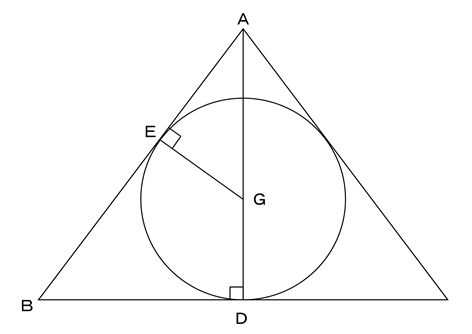
円が三角形に接するとき、半径EGと辺ABは垂直に交わります。
したがって、三角形ABDと三角形AGEは、3つの角の組み合わせが等しくなり、相似形になります。
ここで、AB=40cm、BD=24cm、角ADB=90°となっているので、
AB:AD:BD=5:4:3 となります。
AG:AE:EGも5:4:3になりますので、AG:GE=5:3です。
答え 5:3
(2)
EGもGDも円の半径なので、同じ長さです。
AG=⑤、EG=③とすると、AG+GD=AD=⑧となります。
AD=24÷3×4=32cmより、①=32÷8=4
よって、EG=4×3=12cmです。
答え 12cm
(3)
円Pと円Qの間に直線を引きます。
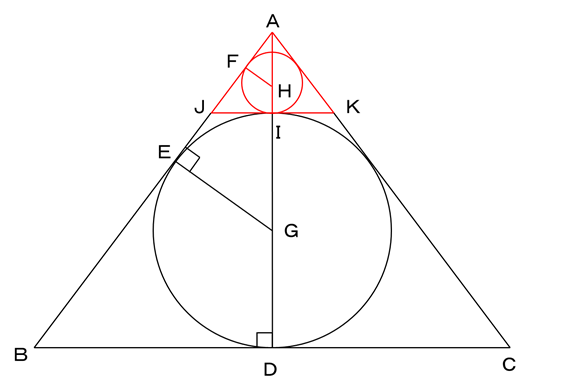
三角形ABCと三角形AJKは相似形となります。
そのため、三角形ABCに円Pが内接しているように、三角形AJKに円Qも内接しています。
(1)(2)より、AD:EG=8:3なので、AI:FHも8:3です。
AD=32cm、IG=GD=12cmより、AI=32-12×2=8cm
よって、FH=3cmです。
答え 3cm
円と直線が接するとき、接する点と半径は垂直に交わる、という円の性質はいろいろな問題でも使います。ぜひおぼえておきましょう。
浅野中入試対策・関連記事一覧
浅野中入試対策・同じ教科(算数)の記事
浅野中入試対策・同じテーマ(合否を分けた一題)の記事
- 社会の合否を分けた一題(2010年度)
- 算数の合否を分けた一題(2012年度)
- 国語の合否を分けた一題(2015年度)
- 算数の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2016年度)
- 社会の合否を分けた一題(2016年度)
- 理科の合否を分けた一題(2016年度)
- 国語の合否を分けた一題(2017年度)
- 社会の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2017年度)
- 理科の合否を分けた一題(2018年度)
- 国語の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2018年度)
- 社会の合否を分けた一題(2018年度)
- 算数の合否を分けた一題(2019年度)
- 理科の合否を分けた一題(2019年度)
- 算数の合否を分けた一題(2020年度)
- 社会の合否を分けた一題(2020年度)
- 国語の合否を分けた一題(2020年度)
- 理科の合否を分けた一題(2020年度)