算数の合否を分けた一題（2016年度）

算数の合否を分けた一題

浅野中入試対策・算数の合否を分けた一題（2016年度）

難易度分類

［１］	（１）Ａ　　（２）Ａ
［２］	（１）Ａ　　（２）Ａ　　（３）Ｂ　　（４）Ａ　　（５）Ａ　　（６）Ｂ　　（７）Ａ
［３］	（１）Ｂ　　（２）Ａ
［４］	（１）Ｂ　　（２）Ｂ
［５］	（１）Ａ　　（２）Ｂ　　（３）Ｂ
［６］	（１）Ａ　　（２）Ｂ　　（３）Ｃ

A…浅野合格を目指すなら必ず得点したい問題
B…着眼点や解法ツールにより正答率・かかる時間に差がつく問題
C…難易度や処理量から判断して、部分点狙いで答案を作成すべき、もしくはとばすべき問題

出題総評

出題形式は、計算２問、一行問題７問、大問４題と例年とほぼ同じ構成になりました。難易度も標準的なものからやや難しいレベルのものが出題され、場合の数・立体表面の最短距離・折り返し図形の角度など、やや処理に時間を要する問題が何問か見られました。例年よりも全体の得点率が下がっており、苦戦した受験生が多かったようです。

問題別寸評

［１］

計算問題が２問出題されました。

（１）

小数と分数の混じった四則計算です。確実に正解したいところです。

（２）

小数の四則逆算問題です。こちらも確実に正解したいところです。

［２］

一行問題７問から成る小問集合です。文章題、場合の数、平面図形と出題単元は多岐に渡っています。

（１）

図形を使った場合の数です。しっかりと樹形図を描いて調べ上げて解いていく問題です。

（２）

速さと周期の問題です。動きや数値が煩雑ではありませんので、こちらは確実に正解しておきたいところです。

（３）

速さと比に関する問題です。道のりの比と速さの比から、移動にかかった時間の比を計算できたかどうかがポイントです。類題を解いたことがある人は解きやすかったものと思われます。

（４）

食塩水のやりとりの問題です。濃さだけを考えていると少し解きにくくなります。このような問題は含まれる食塩の量に着目しましょう。

（５）

ニュートン算の問題です。ニュートン算を苦手にしている受験生も多いのですが、今回の出題は基本の解法をしっかり覚えていれば解きやすい標準的な出題でした。

（６）

砂時計を使った調べ上げの問題です。砂時計の仕組みがわかっていないと少しむずかしかったかもしれません。

（７）

三角形の転がり移動に関する問題です。長方形の周りを１周する様子をきちんと作図できれば解きやすかったのではないでしょうか。このような問題に対しては、普段の学習からきちんと図を描く練習をしているかどうかで差がついてしまいます。

［３］

互除法を用いた、数の性質に関する問題です。過去、開成中や筑駒中でも出題された題材でもあります。

（１）

数は４５８８、２１０９と大きいのですが、問題文の説明通り計算していけば、正解にたどり着くのは難しくはありません。計算力が試される１問でもありました。

（２）

最後に作られた正方形の１辺の長さ＝最大公約数、という知識を知っていればすぐわかる問題ですが、知らなくても問題文で例として挙げられた数値から推測することはできます。
また、（１）がよくわからなくても、互助法を使って最大公約数を求めることはできますので、確実に正解したい問題です。

［４］

立体図形の問題です。今回出題された立体は、正八角柱から三角すいを８個取り除いた、「四角反柱」と呼ばれる立体で、2011年に灘中でも出題されたことがあります。今回は表面積と最短距離に関する問題でしたので、全体の形をイメージできたかどうかがポイントとなります。

（１）

立体の表面積を求める問題です。問題文の説明から、上下に正方形があり、側面は全て三角形になることがわかれば、辺の数値も全て与えられていましたので、解答できたのではないでしょうか。

（２）

側面を１周するときの最短距離を求める問題です。立体上の最短距離の問題は展開図を描いて直線にする、という解法があります。この問題でも側面である８枚の二等辺三角形を並べた図が描ければ、正解できたものと思われます。

［５］

３つのサイコロの目の積に関する場合の数・数の性質の融合問題です。何について、どのように場合分けをして調べられたかで解答する時間にも大きく差がついたものと思われます。

（１）

３つの目の数の積が偶数になる場合を求める問題です。偶数になる場合よりも、奇数になる場合のほうが求めやすいので、余事象を上手く使って解いていきましょう。

（２）

３つの目の数の積が４の倍数になる場合を求める問題です。こちらも４の倍数にならない場合のほうが、（１）の結果を使えるので速く解答することができます。

（３）

３つの目の数の積が６の倍数になる場合を求める問題です。６＝２×３であるため、「６の目が入っている場合」「６の目は入っていないが、偶数と３の倍数の目が１つずつ入っている場合」とに分けて考えていく必要があります。また、サイコロはＡ・Ｂ・Ｃと区別されていますので、答えを求める際に注意が必要となります。

［６］

長方形を折り返した図形に関する角度・面積の問題です。（３）がやや難しく、完答できた受験生は多くなかったのではないでしょうか。

（１）

折り返した部分の角度を求める問題です。図形全体が長方形というところから、平行直線の錯角に気が付けたかどうかがポイントです。

（２）

重なった部分の面積を求める問題です。（１）の答えから、「３０度・６０度・９０度」の特殊角が出てきます。ここもこの数値に気が付けたかどうかがポイントです。

（３）

紙が重なっていない部分と、３枚重なった部分の面積の差を求める問題です。（１）（２）でわかったことを式に表し、また与えられた１３５度という角度から辺の長さを求めていくことで正解にたどりつける難問です。

合否を分けた一題

最初に述べましたが、今年の浅野中の出題形式は例年通りであったものの、図形・場合の数が少し難しく、また解答に時間がかかることから、全体の得点率は下がった形になりました。限られた解答時間の中でどの問題を確実に正解したかが合否を決めるといってもよいでしょう。今回はその中から解き方によって解答時間に差が出る［５］場合の数の問題を説明してまいります。

［５］場合の数

（１）

積が全て偶数となる場合よりも、積が全て奇数となる場合のほうが調べやすいので、こちらを求めて、全ての場合からひいて求めます。
全ての目の出方…６×６×６＝２１６通り
積が奇数になるのは、Ａ、Ｂ、Ｃともに奇数の目（１、３、５）を出したときです。
これは３×３×３＝２７通りになります。
したがって、積が偶数になる目の出方は、２１６－２７＝１８９通りです。

（２）

今度は積が４の倍数になるときです。こちらも４の倍数になるときではなく、「２の倍数だけど４の倍数ではない」場合を考え、（１）の答えからひいて求めます。
積が２の倍数だけど４の倍数ではない場合は、Ａ・Ｂ・Ｃのうちどれか１つが２の倍数だけど４の倍数ではない２か６を出し、残り２つが奇数を出したときです。
まず、目の組合わせを考えると、２×３×３＝１８通りになります。

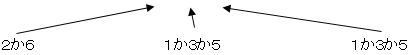
そして、２か６を出すサイコロはＡ、Ｂ、Ｃの３つから選びますので、目の出方は全部で
１８×３＝５４通りになります。
これを（１）の答えである１８９通りからひいて、１８９－５４＝１３５通りになります。

（３）

積が６の倍数になる場合を大きく２つに分けると
（ア）６を出したサイコロが１つ以上ある
（イ）６を出したサイコロはなく、１つが偶数、１つが３の倍数を出している
になります。それぞれの場合について調べていきます。
（ア―１）６を出したサイコロが３つ　１×１×１＝１通り
（ア―２）６を出したサイコロが２つ
目の組合わせは、１×１×５＝５通り
サイコロの組合わせは、６を出していないサイコロをＡ～Ｃから選ぶので３通り
よって、５×３＝１５通り
（ア―３）６を出したサイコロが１つ
目の組合わせは、１×５×５＝２５通り
サイコロの組合わせは、６を出したサイコロをＡ～Ｃから選ぶので３通り
よって、２５×３＝７５通り

（イ）１つのサイコロが「２か４」、別のサイコロが「３」を出しました。
このことに注意して３つの目の組合わせを調べると、
（２、３、１）（２、２、３）（２、３、３）（２、３、４）（２、３、５）
（１、３、４）（３、３、４）（３、４、４）（３、４、５）　の９通り考えられます。
このうち、（２、２、３）（２、３、３）（３、３、４）（３、４、４）はサイコロの選び方が３通りずつ、
（２、３、１）（２、３、４）（２、３、５）（１、３、４）（３、４、５）は
サイコロの選び方が６通り（３×２×１）ずつあります。
４×３＋５×６＝４２通り

したがって全部で、１＋１５＋７５＋４２＝１３３通りになります。

著者：亀井章三

この記事は役にたちましたか？